
2017年“大梦杯”福建省初中数学竞赛试题参考答案 考试时间 2017年3月19日 9∶00-11∶00 满分150分
一、选择题(共5小题,每小题7分,共35分)。每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的。请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分)
1.设a =1
a a
+
的整数部分为( ) A .1 B .2 C .3 D .4 【答案】 B
【解答】由2226a =+-=,知a =
于是1
a a +
=2111()62866a a +=++=+,214()9a a <+<。
因此,1
a a
+
的整数部分为2。
(注:
a ==== 2.方程2
2(
)32
x x x +=-的所有实数根之和为( ) A .1 B .3 C .5 D .7 【答案】 A 【解答】方程2
2(
)32
x x x +=-化为2222(2)3(2)x x x x -+=-。 即3251060x x x -+-=,2(1)(46)0x x x --+=。
解得1x =。经检验1x =是原方程的根。 ∴ 原方程所有实数根之和为1。
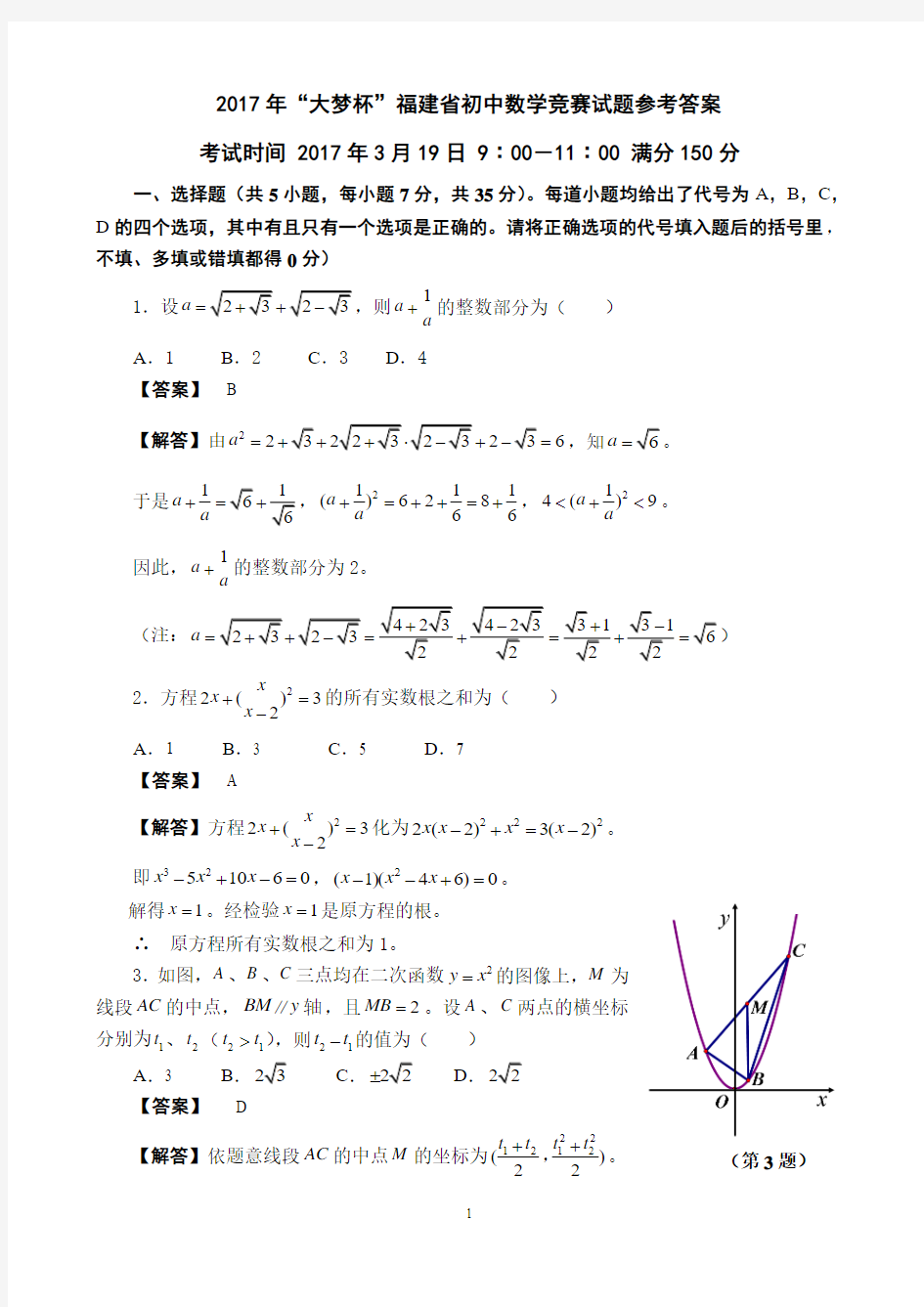
3.如图,A 、B 、C 三点均在二次函数2y x =的图像上,M 为线段AC 的中点,BM y ∥轴,且2MB =。设A 、C 两点的横坐标分别为1t 、2t (21t t >),则21t t -的值为( )
A .3
B .
C .±
D .【答案】 D
【解答】依题意线段AC 的中点M 的坐标为22
1212
()22
t t t t ++,。 (第3题)
由BM y ∥轴,且2BM =,知B 点坐标为22
1212
(2)22t t t t ++-,。 由点B 在抛物线2
y x =上,知22
212122()22
t t t t
++-=。 整理,得2222
121122
2282t t t t t t +-=++,即221()8t t -=。 结合21t t >
,得21t t -=
4.如图,在Rt ABC △中,90ABC ∠=?,D 为线段BC 的中点,E 在线段AB 内,CE 与AD 交于点F 。若A E E F =,且7AC =,3FC =,则c o s A C B ∠的值为( )
A .37 B
. C .314 D
【答案】 B
【解答】如图,过B 作BK AD ∥与CE 的延长线交于点K 。 则由AE EF =可得,EBK EAF AFE BKE ∠=∠=∠=∠。 ∴ EK EB =。
又由D 为BC 中点,得F 为KC 中点。 ∴ 3AB AE EB FE EK KF FC =+=+===。 ∴
BC === ∴
cos 7
BC ACB AC ∠=
=
。 或解:对直线AFD 及BCE △应用梅涅劳斯定理得,
1BD CF EA
DC FE AB
??=。 由D 为线段BC 的中点,知BD DC =。 又AE EF =,因此,3AB CF ==。
结合7AC =,90ABC ∠=?
,利用勾股定理得,BC =
所以,cos 7
BC ACB AC ∠==。
D
B
A E
(第4题)
K
5.如图,O 为ABC △的外接圆的圆心,R 为外接圆半径,且4R =。直线AO 、BO 、CO 分别交ABC △的边于D 、E 、F ,则
111
A D
B E
C F
++的值为( )
A .14
B .13
C .12
D .2
3
【答案】 C
【解答】由条件及等比定理,得
OAB OAC OAB OAC OAB OAC
ABD ACD ABD ACD ABC S S S S S S OA AD S S S S S ++====
+△△△△△△△△△△△, 同理,OAB OBC
ABC
S S OB BE S +=△△△,OBC OAC ABC S S OC CF S +=△△△。 ∴
()()()
2OAB OAC OAB OBC OBC OAC ABC
S S S S S S OA OB OC AD BE CF S +++++++==△△△△△△△。 又4OA OB OC R ====, ∴ 11121
2
AD BE CF R ++==。
二、填空题(共5小题,每小题7分,共35分)
6.记函数223y x x =-+(12x -≤≤)的最大值为M ,最小值为m ,则M m +的值为 。
【答案】 8
【解答】∵ 2223(1)2y x x x =-+=-+,12x -≤≤,
∴ 1x =时,y 取最小值,即2m =;1x =-时,y 取最大值,即6M =。 ∴ 8M m +=。
7.已知二次函数2y ax bx c =++(0a >)的图像与x 轴交于不同的两点A 、B , C 为二次函数图像的顶点,2AB =。若ABC △是边长为2的等边三角形,则a = 。
【答案】
【解答】依题意20ax bx c ++=有两个不同的实根,设为1x ,2x ,则122AB x x =-=。
∵ 12b x x a +=-,12c
x x a
=,
∴ 22
2
21212122
4()()4()44b c b ac x x x x x x a a a
--=+-=--?==,即22
44b ac a -=。 (第5题)
又由22
2()24b b y ax bx c a x c a a =++=+-+,及0a >,
知2
4b c
a
-+=-
即244b a c -=。
∴
24a =
,a =
8.如图,在ABC △中,AD 为BC 边上的高,M 为线段BC 的中点,且
B A D D A M M A ∠=∠=∠。若2AB =,则AB
C △内切圆的半径为 。
【答案】
1
【解答】依题意,易知D 为BM 中点,1
2
DM MC =。 又AM 平分DAC ∠, ∴
1
2
AD MD AC MC ==。结合AD DC ⊥,得30ACD ∠=?。 ∴ 60DAC ∠=?,90BAC ∠=?。 ∴
AC =4BC =。 ∴ ABC △
1=。
9.若二次函数2(43)3y x a x a =+-+(2
3
a ≥
)的图像与直线2y x =-在y 轴左侧恰有1个交点,则符合条件的所有a 的值的和为 。
【答案】
29
12
【解答】依题意,关于x 的方程2(43)32x a x a x +-+=-,即2(42)320x a x a +-+-=恰有1个负根或者两个相等的负根。
有下列三种情形:
(1)方程有两个相等的负根。
则212(42)4(32)0(42)0a a x x a ?=---=?+=--
因此,1a =,3
4
a =
符合要求。 (2)方程两根中一根为零,另一根为负数。
则1212320(42)0
x x a x x a =-=??+=--
B
(第8题)
因此,2
3
a =
符合要求。 (3)方程两根中一根为正数,另一根为负数。 则12320x x a =-<,解得23a <
。不满足23
a ≥。 综合(1)、(2)、(3),得符合条件的a 的值为1,34,2
3
。 因此,符合条件的所有a 的值的和为3229
14312
++=。
10.若正整数n 恰有90个不同的正因数(含1和本身),且在n 的正因数中有7个连续整数,则正整数n 的最小值为 。
【答案】 25200
【解答】∵ 任意连续7个正整数的乘积能被1234567??????整除, ∴ n 的正因数中必定有22,3,5,7这四个数。 ∴ 正整数n 具有形式:1
2
3
4
2
3
5
7
n αααα=????L (1α,2α,3α,4α为正整数,12α≥)
。 由正整数n 恰有90个正因数,知1234(1)(1)(1)(1)90k αααα++++?=,其中k 为正整数。 而90分解为4个大于1的正整数的乘积的分解式只有一种:902335=???。 ∴ 1k =,1234(1)(1)(1)(1)902335αααα++++==???。
∴ n 的最小值为422235725200???=,此时n 有连续正因数1,2,3,4,5,6,7。
三、解答题(共4题,每小题20分,共80分) 11.求方程2220172018x y x +=的正整数解。 【解答】方程化为22201820170x x y -+=。
将方程视为x 的方程,得22222018420174(10092017)y y =-?=-△为完全平方数。…………………… 5分
∴ 2210092017y -为完全平方数。
设22210092017y t -=(t 为非负整数),则22210092017t y -=。 ∴ 2(1009)(1009)2017t t y -+=。 ∵ 2017为质数,
∴ 2017(1009)t -,或2017(1009)t +。…………………… 10分 又t 为非负整数,且1009t ≤。
∴ 1009t =,或1008t =。…………………… 15分 ∴ 0y =(舍去),或1y =。
将1y =代入方程,得2201820170x x -+=,解得1x =,或1017x =。
∴ 原方程的正整数解为11x y =??=?,或20171x y =??=?。…………………… 20分
12.如图,在等腰三角形ABC中,90
ACB
∠=?,M是边AC的中点,D是边BC上一点,直线AD、BM交于点E,且ME MA
=。求证:
(1)BE CD
=;
(2)AC DE AD DB
=。
【解答】(1)如图,连结CE。
由条件知,ME MA MC
==。
∴CE AE
⊥。…………… 5分
∵90
ACB
∠=?,
∴MAE DCE
∠=∠。
∴BED AEM MAE DCE ∠=∠=∠=∠。又EBD CBE
∠=∠,
∴BDE BEC
△∽△。
∴BE DE
BC EC
=。…………… 10分
又由CE AD
⊥,AC CD
⊥,知CDE ACE
△∽△。
∴CD DE AC CE
=。
由此可得,BE DE CD
BC EC AC
==,即
BE CD
BC AC
=。
∵BC AC
=,
∴BE CD
=。…………… 15分
(2)由(1)CE AD
⊥,AC CD
⊥,知CDE ADC
△∽△,
∴CE AC CD AD
=。
又由(1)BDE BEC
△∽△,知DE EC DB EB
=。
结合(1)中BE CD
=,可得AC CE EC DE AD CD EB DB
===。
∴AC DE
AD DB
=。…………… 20分
(第12题)
13.若存在正整数n ,p (6p >)使得3246n n n n p ??
??????+++=????????????????
成立,其中
{}[]x x x =-,[]x 为不超过x 的最大整数。
(1)求p 的最小值;
(2)当p 取最小值时,求使3246n n n n p ??
??????+++=????????????????成立,且2017n ≤的正整数n
的个数。
【解答】(1)∵ 对任意正整数n ,122n ??≤????,344n ??≤????,566n ??≤????,1
n p p p ??-≤????
。
…………………… 5分
∴ 对任意正整数n ,13525
24624612
n n n ??????++≤++=????????????。
∵ 存在正整数n ,p (6p >)使得3246n n n n p ??
??????+++=????????????????成立,
∴ 存在正整数n ,使得2511
31212n p ??≥-=????。
于是,
111
12
p n p p ??-≥≥????,12p ≥。 又11n =时,1111111113511
32461224612
????????+++≤+++=????????????????,
∴ p 的最小值为12。 …………………… 10分
(2)12p =时,由13511
3324624612n n n n p ????????=+++≤+++=????????????????知
122n ??=????,344n ??=????,566n ??=????,111212n ??=????。 ∴ 1211n k =+(k 为非负整数)。
∴ 当p 取最小值12时,当且仅当1211n k =+(k 为非负整数)时,
324612n n n n ????????+++=????????????????
成立。 …………………… 15分 由12112017n k =+≤知,167k ≤。
因此,符合条件的正整数n 有168个。 …………………… 20分
14.将平面上每个点都以红、蓝两色之一染色。证明:
(1)对任意正数a ,无论如何染色平面上总存在两个端点同色且长度为a 的线段; (2)无论如何染色平面上总存在三个顶点同色的直角三角形;
(3)无论如何染色,平面上是否总存在三个顶点同色且面积为2017的直角三角形? 【解答】(1)在平面内任作一个边长为a 的等边ABC △。则ABC △的三个顶点A 、B 、
C 中必有两点同色。
所以,存在两端点同色,且长为a 的线段。
因此,对任意正数a ,无论如何染色平面上总存在两个端点同色且长度为a 的线段。
…………………………………………… 5分
(2)对任意正数a ,如图,设A 、D 同色,且AD a =(由(1)知,A 、D 存在)。 以AD 为直径作圆O ,设ABCDEF 为圆O 的内接正六边形。
若B 、C 、E 、F 中存在一点与A 、D 同色,不妨设点B 与A 、D 同色,则ABD △为直角三角形,其中
90ABD ∠=?,30ADB ∠=?,且三顶点同色。
……………………… 10分
若B 、C 、E 、F 都与A 、D 异色,则B 、C 、E 、
F 四点同色.则BCE △为直角三角形,其中
90BCE ∠=?,30CEB ∠=?,且三顶点同色。
因此,无论如何染色平面上总存在三个顶点同色的直角三角形。……………… 15分 (3)由(2)知,对任意正数a ,无论如何染色总存在斜边长为a ,有一个内角为30?,且三个顶点同色的直角三角形。
当a
=
11())201722S a =??==。
因此,无论如何染色,平面上总存在三个顶点同色且面积为2017的直角三角形。
……………………………………… 20分
A
2006年全国初中数学竞赛试题及参考答案 一、选择题(共5小题,每小题6分,满分30分. 以下每道小题均给出了代号为A,B,C,D的四个选项,其中有且仅有一个选项是正确的. 请将正确选项的代号填入题后的括号里. 不填、多填或错填都得0分) 1.在高速公路上,从3千米处开始,每隔4千米经过一个限速标志牌;并且从10千米处开始,每隔9千米经过一个速度监控仪. 刚好在19千米处第一次同时经过这两种设施,那么第二次同时经过这两种设施的千米数是( ) (A)36(B)37(C)55 (D)90 2.已知,,且,则a的值等于( ) (A)-5(B)5(C)-9(D)9 3.Rt△ABC的三个顶点A,B,C均在抛物线上,并且斜边AB平行于x轴. 若斜边上的高为h,则( ) (A)h<1 (B)h=1 (C)1<h<2 (D)h>2 4.一个正方形纸片,用剪刀沿一条不过任何顶点的直线将其剪成两部分;拿出其中一部分,再沿一条不过任何顶点的直线将其剪成两部分;又从得到的三部分中拿出其中之一,还是沿一条不过任何顶点的直线将其剪成两部分……如此下去,最后得到了34个六十二边形和一些多边形,则至少要剪的刀数是( ) (A)2004 (B)2005 (C)2006 (D)2007 5.如图,正方形ABCD内接于⊙O,点P在劣弧AB上,连结DP,交AC于点Q,若QP=QO,则 的值为( ) (A)(B) (C)(D) 二、填空题(共5小题,每小题6分,满分30分) 6.已知a,b,c为整数,且a+b=2006,c-a=2005. 若a<b,则a+b+c的最大值为___________. 7.如图,面积为的正方形DEFG内接于面积为1的正三角形ABC,其中a,b,c是整数,且b不能被任何质数的平方整除,则的值等于________.
图1 第十四届华罗庚金杯少年数学邀请赛决赛 一、填空题: 1 )计算: 2)如图1所示,在边长为1的小正方形组成的4×4方格图形中,共有25个格点,在以格点为顶点的直角三角形中,两条直角边长分别是1和3的直角三角形共有 个。 3)将七位数1357924重复写287次组成一个2009位数“13579241357924……”。删去 这个新数中所有位于奇数位(从左往右数)上的数字组成一个新数,再删去新数中所有 位于奇数位上的数字,按上述方法一直删下去直到剩下一个数字为止,则最后剩下的数 字是 。 4)如图2所示,在由七个小正方形组成的图形中,直线l 将原图形分为面积相等的两部 分,l 与AB 的交点为E ,与CD 的交点为F ,若线段CF 与线段AE 的长度之和为91厘米, 那么小正方形的边长是 厘米。 5)某班学生要栽一批树苗,若每个人分k 棵树苗,则剩下38棵;若每个学生分配9棵树苗,则还差3棵,那么这个班共有 名学生。 6)已知三个合数A 、B 、C 两两互质,且A ×B ×C =11011×28,那么A +B +C 的最大值是 。 7)方格中的图形符号“◇”,“○”,“▽”“☆”代表填入方格内的数,相同的符号表示相同的数。如图所示。若第一列,第三列,第二行,第四行的四个数的和分别为36,50,41,37。则第三行的四个数的和是 。 8)已知1+2+3+……+n (n >2)的和的个位数为3,十位数为0,则n 的最小值 为 。 二、解答下列各题(要求写出简要过程): 9)下列六个分数的和在哪两个连续自然数之间?
10)2009年的元旦是星期四。问:在2009年,哪几个月的第一天也是星期四?哪几个月有5个星期日? 11)已知a,b,c是三个自然数,且a与b的最小公倍数是60,a与c的最小公倍数是270,求b与c的最小公倍数是多少? 12)在51个连续奇数1,3,5,……,101中选取k个数,使得他们的和为1949,那么k的最大值是多少? 三、解答下列各题(要求写出详细解答过程) 13)如图所示,在梯形ABCD中,AB∥CD,对角线AC,BC相交于O点,已知AB=5,CD=3,且梯形ABCD的面积为4,求三角形OAB的面积。 14)如下算式,汉字代表1至9这9个数字,不同的汉字代表不同的数字。若“祝”字和“贺”字分别代表数字“ 4”和“8”,求出“华杯赛”所代表的整数。
2016年“大梦杯”福建省初中数学竞赛试题参考答案 考试时间 2016年3月13日 9∶00-11∶00 满分150分 一、选择题(共5小题,每小题7分,共35分)。每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的。请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分) 1.在平面直角坐标系xOy 中,已知点(02)B ,,点A 在x 轴正半轴上且30BAO ∠=?。将 OAB △沿直线AB 折叠得CAB △,则点C 的坐标为( ) A .(13), B .(33), C .(33), D .(31), 【答案】 B 【解答】如图,设CD x ⊥轴于点D 。 依题意,23CA OA ==,260CAO BAO ∠=∠=?。 所以,3CD =,3AD =,3OD =。 因此,点C 的坐标为(33), 。 2.若实数a ,b 满足232a a +=,232b b +=,且a b ≠,则22(1)(1)a b ++=( ) A .18 B .12 C .9 D .6 【答案】 A 【解答】依题意,a ,b 为方程2320x x +-=的两个不同实根。 因此,由韦达定理得,3a b +=-,2ab =-。 []22(1)(1)(123)(123)9(1)(1)91()9(132)18a b a b a b a b ab ++=+-+-=--=-++=+-=。 或解:222222222(1)(1)11()2194418a b a b a b a b ab a b ++=+++=++-+=+++=。 3.若关于x 的方程22240224 x x x a x x x +-+++=-+-只有一个实数根,则符合条件的所有实数a 的值的总和为( ) A .6- B .30- C .32- D .38- 【答案】 D 【解答】方程 22240224 x x x a x x x +-+++=-+-化为22480x x a +++= ……………… ① 若方程①有两个相等实根,则168(8)0a =-+=△,6a =-。 6a =-时,方程①的根121x x ==-,符合要求。 若2x =是方程①的根,则8880a +++=,24a =-,此时,方程①的另一个根为4x =-,符合要求。 若2x =-是方程①的根,则8880a -++=,8a =-,此时,方程①的另一个根为0x =,符合要求。
1991年全国初中数学联合竞赛决赛试题 第一试 一、选择题 本题共有8个小题,每小题都给出了(A )、(B )(C )、(D )四个答案结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内. 1. 设等式y a a x a y a a x a ---=-+-)()(在实数范围内成立,其中a ,x ,y 是 两两不同的实数,则2 22 23y xy x y xy x +--+的值是 (A )3 ; (B )31; (C )2; (D )3 5 . 答( ) 2. 如图,AB ‖EF ‖CD ,已知AB =20,CD =80,BC =100,那么EF 的值是 (A ) 10; (B )12; (C ) 16; (D )18. 答( ) 3. 方程012=--x x 的解是 (A ) 251±; (B )25 1±-; (C ) 251±或251±-; (D )2 5 1±-±. 答( ) 4. 已知:)19911991(2 11 1 n n x --=(n 是自然数).那么n x x )1(2+-,的值是 (A)11991-; (B)11991--; (C)1991)1(n -; (D)11991)1(--n . 答( ) 5. 若M n 1210099321=?????Λ,其中M为自然数,n 为使得等式成立的最大的自然数,则M (A)能被2整除,但不能被3整除; (B)能被3整除,但不能被2整除; (C)能被4整除,但不能被3整除; (D)不能被3整除,也不能被2整除.
答( ) 6. 若a ,c ,d 是整数,b 是正整数,且满足c b a =+,d c b =+,a d c =+,那么 d c b a +++的最大值是 (A)1-;(B)5-;(C)0;(D)1. 答( ) 7. 如图,正方形OPQR 内接于ΔABC .已知ΔAOR 、ΔBOP 和ΔCRQ 的面积分别是11=S , 32=S 和13=S ,那么,正方形OPQR 的边长是 (A)2;(B)3;(C)2 ;(D)3. 答( ) 8. 在锐角ΔABC 中, 1= AC ,c AB =,ο60=∠A ,ΔABC 的外接圆半径R ≤1,则 (A)21< c < 2 ; (B)0< c ≤2 1 ; 答( ) (C )c > 2; (D )c = 2. 答( ) 二、填空题 1.E是平行四边形ABCD 中BC 边的中点,AE 交对角线BD 于G ,如果ΔBEG 的面积是1,则平行四边形ABCD 的面积是 . 2.已知关于x 的一元二次方程02=++c bx ax 没有实数解.甲由于看错了二次项系数,误求得两根为2和4;乙由于看错了某一项系数的符号,误求得两根为-1和4,那么,=+a c b 32 . 3.设m ,n ,p ,q 为非负数,且对一切x >0,q p n m x x x x )1(1)1(+=-+恒成立,则 =++q p n m 22)2( . 4.四边形ABCD 中,∠ ABC ο135=,∠BCD ο120=,AB 6=,BC 35-=, CD = 6,则AD = . 第二试 1 1=S 3S =1 32=S
华罗庚杯六年级数学竞赛试题: 华罗庚杯六年级数学竞赛试题:一、认真思考、填一填。(18分,每空0.5分) 1、猪八戒的电话号码是4个8、3个0组成的7位数,且只能读出一个零的最小数,是( )。 2、一个多位数,省略万位后面的尾数约是6万,这个多位数最大可能是( )、最小可能是( )。 3、 =( ):( )=0.375=6 ÷( )=( )% 4、a是b的7倍,b就是a的( )。2个白球,2个黄球装在一个口袋里,任意摸一个( )是红球。 5、被减数,减数与差的和是4 ,被减数是( )。被除数+除数+商=39,商是3,被除数是( )。 6、甲、乙、丙三个数之和是194,乙数是甲数的1.2倍,丙是乙的1.4倍,甲是( )。 7、圆的周长与直径的比是( )。上5层楼花1.2分钟,上8层楼要( )分钟, 8、任意写出两个大小相等,精确度不一样的两个小数( )、( )。 9、甲数比乙数多25,乙数比丙数多75,甲数比丙数多( )。 10.、三个连续偶数的和是a,最小偶数是( )。 11、的分母增加10,要使分数值不变,分子应增加( )。 12、小红比小刚多a元,那么小红给小刚( )元,两人的钱数
相等。 13、一本故事书页,小华每天看m页,看了y天,还剩( )页未看。 14、a的与b的相等,那么a与b的比值是( )。 15、甲÷乙=15,甲乙两数的最大公因数是( ),最小公倍数是( )。 16、一个数的小数点向左移动一位,比原来的数小了2.25,原数是( )。 17、:6的前项乘4,要使比值不变,后项应该加上( )。 18、是把整体“1”平均分成( )份,表示其中的( )份,也可以说把( )平均分成( ) ,份表示其中的( )份,或许说( )是( )的。 二、我是聪明的小法官(对的√、错的×)(5分,每空0.5分) 1、40500平方米=40.5公顷 ( ) 2、统计一个病人的体温最好选择条形统计图。 ( ) 3、小刚生于1995年2月29日。 ( ) 4、圆的半径是,求半圆周长公式是 ( +2)。 ( ) 5、与20%表示意义完全相同。 ( ) 6、一根绳子长剪成两段,第一段长米,第二段占全长的, 第二段绳子长( )米 7、众数的特点是用来代表一组数据的“多数水平”。( ) 8、甲数比乙数多,则乙数比甲数少20% 。 ( ) 9、4900÷400=49÷4=12……1 ( ) 10、同样长的铁丝,围成正方形和围成圆形,它们的面积一
大梦杯福建省初中数学竞赛试题参考答案及评分标 准 The latest revision on November 22, 2020
2018年“大梦杯”福建省初中数学竞赛试题 考试时间 2018年3月18日 9∶00-11∶00 满分150分 一、选择题(共5小题,每小题7分,共35分)。每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的。请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分) 1.若关于x 的方程244310x mx m +--=有两个相等的实数根,则32442m m m ++-的值为( ) A .3- B .2- C .1- D .1 2.如图,ABCD 、DEFG 都是正方形,边长分别为m 、n (m n <)。坐标原点O 为 AD 的中点,A 、D 、E 在y 轴上。若二次函数2y ax =的图像过C 、F 两点,则n m =( ) A .31+ B .21+ C .231- D .221- 3.如图,G 为ABC △的重心,点D 在CB 延长线上,且1 2 BD BC =,过D 、G 的直线交AC 于点E ,则 AE AC =( ) A .2 5 B .3 5 C . 3 7 D . 47 4.如图,H 、O 分别为ABC △的垂心、外心,45BAC ∠=?,若ABC △外接圆的半径 为2,则AH =( ) A .23 B .22 C .4 D .31+ 5.满足方程22419151x xy y -+=的整数对()x y , 有( ) H O B C A (第4题图) (第2题图) E G B D (第3题图)
1991年全国初中数学联合竞赛决赛试题 第一试 一、选择题 本题共有8个小题,每小题都给出了(A )、(B )(C )、(D )四个答案结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内. . 设等式y a a x a y a a x a ---=-+-)()(在实数范围内成立,其中a ,x ,y 是两两不 同的实数,则22223y xy x y xy x +--+的值是 (A )3 ; (B )31; (C )2; (D )35 . 答( ) . 如图,AB ‖EF ‖CD ,已知AB =20,CD =80,BC =100,那么EF 的值是 (A ) 10; (B )12; (C ) 16; (D )18. 答( ) . 方程0 12=--x x 的解是 (A )251±; (B )25 1±-; (C )251±或251±-; (D )251±-± . 答( ) . 已知:)19911991(21 1 1n n x --=(n 是自然数).那么 n x x )1(2+-,的值是 (A)11991-; (B)1 1991--; (C)1991)1(n -; (D)1 1991)1(--n . 答( ) . 若M n 1210099321=????? ,其中M为自然数,n 为使得等式成立的最大的自然数,则M (A)能被2整除,但不能被3整除; (B)能被3整除,但不能被2整除; (C)能被4整除,但不能被3整除; (D)不能被3整除,也不能被2整除. 答( ) . 若a ,c ,d 是整数,b 是正整数,且满足c b a =+,d c b =+,a d c =+,那么 d c b a +++的最大值是 (A)1-;(B)5-;(C)0;(D)1. 答( ) . 如图,正方形OPQR 内接于ΔABC .已知ΔAOR 、ΔBOP 和ΔCRQ 的面积分别是11=S ,32=S 和 1 3=S ,那么,正方形OPQR 的边长是 (A)2;(B)3;(C)2 ;(D)3. 答( ) 1 1=S
2018年“大梦杯”福建省初中数学竞赛试题参考答案及评分标准 一、选择题(共5小题,每小题7分,共35分) 01.若关于x 的方程244310x mx m +--=有两个相等的实数根,则32 442m m m ++-的值为( A ) A .3- B .2- C .1- D .1 【解答】依题意,2 1616(31)0m m D =++=,∴2 310 m m ++=,∴231m m =--,2 31m m +=-。 ∴3 2 2 2 442(31)44232123m m m m m m m m m ++-=--++-=+-=--=-。 02.如图,正方形ABCD 和正方形DEFG 的边长分别为()m n m n <、 。原点O 为AD 的中点,A D E 、、在y 轴上。若二次函数2 y ax =的图像经过C F 、 两点,则n m =( B ) A 1 B 1 C .1 D .1 【解答】依题意,点C 的坐标为()2m m ,,点F 的坐标为()2 m n n -+,。 由二次函数2 y ax =的图像经过C F 、两点得22 2()2 m am m n a n ì=??í?+=-??, 消去a 得22 20n mn m --=。 ∴2210n n m m 骣-?=琪桫 ,解得1n m =(舍负根)。∴ n m =03.如图,G 为ABC △的重心,点D 在CB 延长线上且12BD BC =,直线 A .25 B .35 C .37 D .4 7 ( D ) F B D F B 【解答】如图,连AG ,并延长交BC 于点F 。 ∵G 为ABC △的重心且12BD BC = ,∴F 为BC 中点且21 AG GF =,DB BF FC ==。 过点F 作FM DE ∥,交AC 于点M ,则13CM CF CE CD ==,2 1 AE AG EM GF ==。 设CM k =,则3CE k =,2EM k =,4AE k =,∴7AC k =,44 77AE k AC k ==。 另解:如图,连AG ,并延长交BC 于点F 。∵G 为ABC △的重心且1 2 BD BC =, ∴F 为BC 中点且21AG GF =,DB BF FC ==,∴23FD DC =,2 1 AG GF =。 在AFC △中,由梅涅劳斯定理得1FD CE AG DC EA GF 鬃=,22131CE EA 鬃=,34CE EA =,∴4 7 AE AC =。 (第03题答题图2) (第03题答题图1) (第03题图)
2017年全国初中数学联赛决赛试卷B (3月26日 上午8:45—11:15) (本试卷由李庄中学 况永胜(QQ:369132130录入) 一、选择题(本题满分42分,每小题7分) 本题共有6小题,每题均给出了代号为A 、B 、C 、D 的四个答案,其中有且仅有一个是正确的。将你选择的答案的代号填在题号的括号内,每小题选对得7分;不选、错选或选出的代号字母超过一个(不论是否写在括号内),一律得0分。 1、若q 是质数,且q +1 是完全平方数,就称q 为P 型质数,则P 型质数的个数是( ) A 、0 B 、1 C 、2 D 、无数个 2、已知k 为正实数,一次函数y =kx +1与反比例函数y = k x 的图象交于A (x 1,y 1),B (x 2,y 2)两点,若||x 1-x 2=5,则k 的值是( ) A 、1 B 、 2 C 、 3 D 、2 3、已知AD 、BE 、CF 为锐角△ABC 三边上的高,若AB =26,EF BC = 513, 则BE 的长度是( ) A 、10 B 、12 C 、13 D 、24 4、在梯形ABCD 中,AB ∥CD ,∠ABC =90°,E 是腰AD 的中点,若EC = 13,AB +BC +CD =226,则∠BCE = ( ) A 、30° B 、45° C 、60° D 、75° 5、若实数k 使得关于x 的方程(x 2–1)(kx 2–6x –8)=0恰有三个不同的实数根,则称k 为“好数”, 则“好数”k 的个数是( ) A 、1 B 、2 C 、3 D 、4 6.记正整数m 的各位数字之和为S (m ),比如S (2017)=2+0+1+7=10,现从1,2,3,…,2016,2017这2017个正整数中,任意取出n 个不同的数,都能在这n 个数中找到a 1,a 2,…,a 7,a 8, 使得S (a 1) = S (a 2)= …= S (a 7) = S (a 8),则正整数n 的最小值是( ) A 、185 B 、187 C 、189 D 、191 二、填空题(本大题满分28分,每小题7分) 本题共有4小题,要求直接将答案写在横线上. 7、若x =3–2,则 –x 2–2x x 2–1÷ ( 1||x +1 + 1||x –1 )的值是 8、在平面直角坐标系中,点O (0,0)、A (0,6)、B (-3,2)、C (-2,9),点P 为线段OA (含端点)上任意一点,则PB +PC 的最小值是 9、有4只杯口全朝上的茶杯,现在每次翻转3只,翻动的茶杯允许再翻,经过n 次翻动后,使得杯口全朝下,则正整数n 的最小值是 (注:所谓一只茶杯的一次翻转是指将该茶杯的杯口朝上(下)翻为杯口朝下(上)) 10、设A 、B 为抛物线y = x 2上两点,该两点在y 轴两侧,满足AB =4,记△AOB 的面积为S ,其中O 为坐标原点,则S 的最大值是 三、解答题(本题满分20分) 11、设a 、b 、c 是任意三个互不相等的有理数,证明: 1(a –b )2 + 1(b –c )2 + 1(c –a )2 是有理数.
初三数学竞赛试题 4、某商店经销一批衬衣,进价为每件m元,零售价比进价高a%,后因市场的变化,该店把零售价调整为原来零售价的b%出售,那么调价后每件衬衣的零售价是() A. m(1+a%)(1-b%)元 B. m?a%(1-b%)元 C. m(1+a%)b%元 D. m(1+a%b%)元 解:选C。设全天下雨a天,上午晴下午雨b天,上午雨下午晴c天,全天晴d天。由题可得关系式a=0①,b+d=6②,c+d=5③,a+b+c=7④,②+③-④得2d-a=4,即d=2,故b=4,c=3,于是x=a+b+c+d=9。 解:出发1小时后,①、②、③号艇与④号艇的距离分别为 各艇追上④号艇的时间为 对>>>有,即①号艇追上④号艇用的时间最小,①号是冠军。 解:设开始抽水时满池水的量为,泉水每小时涌出的水量为,水泵每小时抽水量为,2小时抽干满池水需n台水泵,则 由①②得,代入③得: ∴,故n的最小整数值为23。 答:要在2小时内抽干满池水,至少需要水泵23台 解:设第一层有客房间,则第二层有间,由题可得 由①得:,即 由②得:,即 ∴原不等式组的解集为 ∴整数的值为。
答:一层有客房10间。 解:设劳动竞赛前每人一天做个零件 由题意 解得 ∵是整数∴=16 (16+37)÷16≈3.3 故改进技术后的生产效率是劳动竞赛前的3.3倍。 初中数学竞赛专项训练(2) (方程应用) 一、选择题: 答:D。 解:设甲的速度为千米/时,乙的速度为千米/时,根据题意知,从出发地点到A的路程为千米,到B的路程为千米,从而有方程: ,化简得,解得不合题意舍去)。应选D。 答:C。 解:第k档次产品比最低档次产品提高了(k-1)个档次,所以每天利润为 所以,生产第9档次产品获利润最大,每天获利864元。 答:C。 解:若这商品原来进价为每件a元,提价后的利润率为, 则解这个方程组,得,即提价后的利润率为16%。 答:B。
第十届华罗庚金杯初赛试题 1. 2005年是中国伟大航海家郑和首次下西洋600周年, 西班牙伟大航海家哥伦布首次远洋航行是在1492 年. 问这两次远洋航行相差多少年? 2. 从冬至之日起每九天分为一段, 依次称之为一九, 二九, …, 九九. 2004年的冬至为12月21日, 2005年的立春是2月4日. 问立春之日是几九的第几天? 3. 左下方是一个直三棱柱的表面展开图,其中,黄色和绿色的部分都是边长等于 1 的正方形. 问这个直三棱柱的体积是多少? 4. 爸爸、妈妈、客人和我四人围着圆桌喝茶. 若只考虑每人左邻的情况,问共有多少种不同的入座方法? 5. 在奥运会的铁人三项比赛中,自行车比赛距离是长跑的 4 倍,游泳的距离是自行车的,长跑与游泳的距离之差为8.5千米. 求三项的总距离. 6. 如右图,用同样大小的正三角形,向下逐次拼接出更大的正三角形. 其中最小的三角形顶点的个数(重合的顶点只计一次)依次为: 3, 6, 10, 15, 21, … 问这列数中的第 9 个是多少? 7. 一个圆锥形容器甲与一个半球形容器乙,它们圆形口的直径与容器的高的尺寸如图所示. 若用甲容器取水来注满乙容器, 问: 至少要注水多少次?
8. 100 名学生参加社会实践, 高年级学生两人一组, 低年级学生三人一组,共有 41组. 问: 高、低年级学生各多少人? 9. 小鸣用48元钱按零售价买了若干练习本. 如果按批发价购买, 每本便宜 2元, 恰好多买4本. 问: 零售价每本多少元? 10. 不足100 名同学跳集体舞时有两种组合:一种是中间一组5人,其他人按8人一组围在外圈;另一种是中间一组8人,其他人按5人一组围在外圈. 问最多有多少名同学? 11. 输液100毫升, 每分钟输2.5毫升. 请你观察第12分钟时吊瓶图像中的数据, 回答整个吊瓶的容积是多少毫升? 12. 两条直线相交所成的锐角或直角称为两条直线的“夹角”. 现平面上有若干条直线,它们两两相交,并且“夹角”只能是 300, 600 或 900. 问: 至多有多少条直线? 初赛试题答案 1 87年. 2 六九的第一天.
2017年“大梦杯”福建省初中数学竞赛试题参考答案 考试时间 2017年3月19日 9∶00-11∶00 满分150分 一、选择题(共5小题,每小题7分,共35分)。每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的。请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分) 1.设a =1 a a + 的整数部分为( ) A .1 B .2 C .3 D .4 【答案】 B 【解答】由2226a =+-=,知a = 于是1 a a + =2111()62866a a +=++=+,214()9a a <+<。 因此,1 a a + 的整数部分为2。 (注: a ==== 2.方程2 2( )32 x x x +=-的所有实数根之和为( ) A .1 B .3 C .5 D .7 【答案】 A 【解答】方程2 2( )32 x x x +=-化为2222(2)3(2)x x x x -+=-。 即3251060x x x -+-=,2(1)(46)0x x x --+=。 解得1x =。经检验1x =是原方程的根。 ∴ 原方程所有实数根之和为1。 3.如图,A 、B 、C 三点均在二次函数2y x =的图像上,M 为线段AC 的中点,BM y ∥轴,且2MB =。设A 、C 两点的横坐标分别为1t 、2t (21t t >),则21t t -的值为( ) A .3 B . C .± D .【答案】 D 【解答】依题意线段AC 的中点M 的坐标为22 1212 ()22 t t t t ++,。 (第3题)
由BM y ∥轴,且2BM =,知B 点坐标为22 1212 (2)22t t t t ++-,。 由点B 在抛物线2 y x =上,知22 212122()22 t t t t ++-=。 整理,得2222 121122 2282t t t t t t +-=++,即221()8t t -=。 结合21t t > ,得21t t -= 4.如图,在Rt ABC △中,90ABC ∠=?,D 为线段BC 的中点,E 在线段AB 内,CE 与AD 交于点F 。若A E E F =,且7AC =,3FC =,则c o s A C B ∠的值为( ) A .37 B . C .314 D 【答案】 B 【解答】如图,过B 作BK AD ∥与CE 的延长线交于点K 。 则由AE EF =可得,EBK EAF AFE BKE ∠=∠=∠=∠。 ∴ EK EB =。 又由D 为BC 中点,得F 为KC 中点。 ∴ 3AB AE EB FE EK KF FC =+=+===。 ∴ BC === ∴ cos 7 BC ACB AC ∠= = 。 或解:对直线AFD 及BCE △应用梅涅劳斯定理得, 1BD CF EA DC FE AB ??=。 由D 为线段BC 的中点,知BD DC =。 又AE EF =,因此,3AB CF ==。 结合7AC =,90ABC ∠=? ,利用勾股定理得,BC = 所以,cos 7 BC ACB AC ∠==。 D B A E (第4题) K
绝密★启用前 2015-2016学年度???学校12月月考卷 试卷副标题 注意事项: 1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上 第I 卷(选择题) 请点击修改第I 卷的文字说明 一、选择题(题型注释) 1.船在江中顺水航行与逆水航行的速度之比为7:2,那么它在两港间往返一次的平均速度与顺 水速度之比为( )。 (A) 14 7 (B) 14 9 (C) 92 (D) 94 。 【答案】D 【解析】分析:设出顺水速度和逆水速度,那么可让总路程÷总时间求得平均速度,相比即可. 解答:解:设船在江中顺水速度为7x ,则逆水速度为2x ,一次的航程为1. ∴平均速度= 2117x 2x += 28 9 x , ∴它在两港间往返一次的平均速度与顺水速度之比为 289 x :7x=94. 故选D . 2. 如右图所示,三角形ABC 的面积为1cm 2 。AP 垂直∠B 的平分线BP 于P 。则与三角形PBC 的面积相等的长方形是( )。 【答案】B 【解析】分析:过P 点作PE ⊥BP ,垂足为P ,交BC 于E ,根据AP 垂直∠B 的平分线BP 于P ,即可求出△ABP ≌△BEP ,又知△APC 和△CPE 等底同高,可以证明两三角形面 0.5cm 0.5cm 0.9cm 1.0cm 1.1cm 1.2cm (A) (B) (C) (D) B
试卷第2页,总5页 订 … … … … ○ … … … … 线 … … … … ○ 内 ※ ※ 答 ※ ※ 题 ※ ※ 订 … … … … ○ … … … … 线 … … … … ○ 积相等,即可证明三角形PBC的面积. 解答:解:过P点作PE⊥BP,垂足为P,交BC于E, ∵AP垂直∠B的平分线BP于P, ∠ABP=∠EBP, 又知BP=BP,∠APB=∠BPE=90°, ∴△ABP≌△BEP, ∴AP=PE, ∵△APC和△CPE等底同高, ∴S△APC=S△PCE, ∴三角形PBC的面积=1 2 三角形ABC的面积= 1 2 cm2, 选项中只有B的长方形面积为1 2 cm2, 故选B. 3.设a,B的解集为x x的不等式bx-a>0的解集是( )。 (A) x x
1 2016年“大梦杯”福建省初中数学竞赛试题参考答案 考试时间 2016年3月13日 9∶00-11∶00 满分150分 一、选择题(共5小题,每小题7分,共35分)。每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的。请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分) 1.在平面直角坐标系xOy 中,已知点(02)B ,,点A 在x 轴正半轴上且30BAO ∠=?。将 OAB △沿直线AB 折叠得CAB △,则点C 的坐标为( ) A .(1 B .3) C .(3 D .1) 2.若实数a ,b 满足232a a +=,232b b +=,且a b ≠,则22(1)(1)a b ++=( ) A .18 B .12 C .9 D .6 3.若关于x 的方程22240224 x x x a x x x +-+++=-+-只有一个实数根,则符合条件的所有实数a 的值的总和为( ) A .6- B .30- C .32- D .38- 4.如图,在ABC △中,6AB =,3BC =,7CA =,I 为ABC △的内心,连接CI 并延长交AB 于点D 。记CAI △的面积为m , DAI △的面积为n ,则 m n =( ) A .32 B .43 C .53 D .74 5.已知x ,y 为实数,且满足2244x xy y -+=,记224u x xy y =++的最大值为M ,最小 A B C D I
2 值为m ,则M m +=( ) A .403 B .64 15 C .13615 D .315 二、填空题(共5小题,每小题7分,共35分) 6.在平面直角坐标系内有两点(11)A ,,(23)B ,,若一次函数2y kx =+的图像与线段AB 有公共点,则k 的取值范围为 。 7.如图,在ABC △中,D 为BC 边上一点,E 为线段AD 上一点,延长BE 交AC 于点F 。若 25BD BC =,12AE AD =,则AF AC = 。 8.设1x ,2x ,3x ,…,n x 是n 个互不相同的正整数,且1232017n x x x x ++++=L ,则n 的最大值是 。 9.如图,AB 是O ⊙的直径,AC 是O ⊙的切线,BC 交O ⊙于E 点,若 OA CE =,则AE AB = 。 E O A B C F B C A D E
中国教育学会中学数学教学专业委员会 全国初中数学竞赛试题 一、选择题(共5小题,每小题6分,共30分.) 1(甲).如果实数a,b,c在数轴上的位置如图所示,那 22 ||()|| a a b c a b c ++-++可以化简为(). (A)2c a-(B)22 a b -(C)a-(D)a 1(乙).如果22 a=- 1 1 1 2 3a + + + 的值为(). (A)2 -(B)2(C)2 (D) 22 2(甲).如果正比例函数y = ax(a ≠ 0)与反比例函数 y = x b(b ≠0 )的图象有两个交点,其中一个交点的坐标为(-3,-2),那么另一个交点的坐标为(). (A)(2,3)(B)(3,-2)(C)(-2,3) (D)(3,2) 2(乙).在平面直角坐标系xOy中,满足不等式x2+y2≤2x +2y的整数点坐标(x,y)的个数为(). (A)10 (B)9 (C)7 (D)5 3(甲).如果a b,为给定的实数,且1a b <<,那么
1121 a a b a b ++++,, ,这四个数据的平均数与中位数之差的 绝对值是( ). (A )1 (B ) 214a - (C )12 (D )1 4 3(乙).如图,四边形ABCD 中,AC ,BD 是对角线, △ABC 是等边三角形.30ADC ∠=?,AD = 3,BD = 5, 则CD 的长为( ). (A )23 (B )4 (C )52 (D )4.5 4(甲).小倩和小玲每人都有若干面值为整数元的人民币.小倩对小玲说:“你若给我2元,我的钱数将是你的n 倍”;小玲对小倩说:“你若给我n 元,我的钱数将是你的2倍”,其中n 为正整数,则n 的可能值的个数是( ). (A )1 (B )2 (C )3 (D )4 4(乙).如果关于x 的方程 2 0x px q p q --=(,是正整数)的正根小于3, 那么这样的方程的 个数是( ). (A ) 5 (B ) 6 (C ) 7 (D ) 8 5(甲).一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,3,4,5,6.掷两次骰子,设其朝上的面上的两个数字之和除以4的余数分别是0,1,2,3的概率为0123p p p p ,,,,则 0123p p p p ,,,中最大的是( ). (A )0p (B )1p (C )2p (D )3p 5(乙).黑板上写有1 11123100 , , ,, 共100个数字.每次操作先从黑板上的数中选取2个数 a b ,,然后删去a b ,,并在黑板上写上数a b ab ++,则经过99次操作后,黑板上剩下的数 是( ). (A )2012 (B )101 (C )100 (D )99 二、填空题(共5小题,每小题6分,共30分) 6(甲).按如图的程序进行操作,规定:程序运行 从“输入一个值x ”到“结果是否>487?”为一次
2017年第二十二届“华罗庚金杯”少年数学邀请赛初赛试卷(小 高组) 一、选择题(每小题10分,共60分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.) 1.(10分)两个有限小数的整数部分分别是7和10,那么这两个有限小数的积的整数部分有()种可能的取值. A.16 B.17 C.18 D.19 2.(10分)小明家距学校,乘地铁需要30分钟,乘公交车需要50分钟.某天小明因故先乘地铁,再换乘公交车,用了40分钟到达学校,其中换乘过程用了6分钟,那么这天小明乘坐公交车用了()分钟. A.6 B.8 C.10 D.12 3.(10分)将长方形ABCD对角线平均分成12段,连接成如图,长方形ABCD 内部空白部分面积总和是10平方厘米,那么阴影部分面积总和是()平方厘米. A.14 B.16 C.18 D.20 4.(10分)请在图中的每个方框中填入适当的数字,使得乘法竖式成立.那么乘积是() A.2986 B.2858 C.2672 D.2754
5.(10分)在序列20170…中,从第5 个数字开始,每个数字都是前面4 个数字和的个位数,这样的序列可以一直写下去.那么从第 5 个数字开始,该序列中一定不会出现的数组是() A.8615 B.2016 C.4023 D.2017 6.(10分)从0至9中选择四个不同的数字分别填入方框中的四个括号中,共有()种填法使得方框中话是正确的. 这句话里有()个数大于1,有()个数大于2,有()个数大 于3,有()个数大于4. A.1 B.2 C.3 D.4 二、填空题(每小题10分,共40分) 7.(10分)若[﹣]×÷+2.25=4,那么A 的值是. 8.(10分)如图中,“华罗庚金杯”五个汉字分别代表1﹣5这五个不同的数字.将各线段两端点的数字相加得到五个和,共有种情况使得这五个和恰为五个连续自然数. 9.(10分)如图中,ABCD是平行四边形,E为CD的中点,AE和BD的交点为F,AC和BE的交点为H,AC和BD的交点为G,四边形EHGF的面积是15平方厘米,则ABCD的面积是平方厘米.
四年级数学华罗庚杯奥林匹克竞赛 一、简算与计算(每小题4分,共16分) 1. 395-283+154+246-117 2. 8795-4998+2994-3002-2008 3. 125×198÷(18÷8) 4. 454+999×999+545 二、填空题(每题4分,共44分) 1. 表一表二是按同一规律排列的两个方格表,那么表二的空白方格中应填的数是( )。 2. 一支钢笔能换3支圆珠笔,4支圆珠笔能换7支铅笔,那么4支钢笔能换( )支铅笔。 3. 两数之和是616,其中一个数的最后一位数字是0,如果把0去掉,就与另一个数相同,这两个数的差是( )。 4. 右图中一共有几个三角形( )。 5. 一个六位数,个位数是7,十万位上的数是9,任意相邻的三个数位上数的和都是20,这个六位数是( )。 6. 下面两组数是同学们玩24点扑克牌游戏中四张牌上的四个数字,请你选用+、-、×、÷、( )组成等式。 (1) 1、4、7、7 (2)1、2、7、7 15 3 5 5 2 3 1 2 24 4 6 6 2 4 4 2 2 表一 表二
=24; = 24 7. 一个老人等速在公路上散步,从第1根电线杆走到第15根,用了15分钟;这个老人 如果走30分钟应走到第( )根电线杆。 8. 星期天妈妈要做好多事情,擦玻璃要20分钟,收拾厨房要15分钟,洗脏脱衣服的领口和袖口要10分钟,打开全自动洗衣机洗衣服要40分钟,晾衣服要10分钟。妈妈干完所有这些事最少要 分钟。 9. 青蛙白天向上爬3米,晚上滑下2米,青哇从井底爬到井外(井高10米)至少需要( )天( )夜。 10. 观察下图数字间的关系,在圆圈内填上适当的数。 11. 小鹏在期中考试时,语文得79分,常识得90分,数学考得最好。已知小鹏的三科平均分是一个偶数,那么小鹏数学得 分。(注:各科的满分均为100分) 三、解答题(每题8分,共40分) 1. 王雪读一本故事书,第一天读了8页,以后每天都比前一天多读3页,最后一天读了32页正好读完。她一共读了多少天? 2. 甲乙两车同时从东西两地相向出发,甲车每小时行56千米,乙车每小时行48千米,两车在离中点32千米处相遇。求东西两地间的路程是多少千米? 2 4 6 16 42 10
2017年全国初中数学联合竞赛试题 说明:评阅试卷时,请依据本评分标准.第一试,选择题和填空题只设7分和0分两档;第二试各题,请按照本评分标准规定的评分档次给分.如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准划分的档次,给予相应的分数. 第一试(A) 一、选择题(本题满分42分,每小题7分) 1.已知实数a ,b ,c 满足2a +13b +3c =90,3a +9b +c =72,则3b +c a +2b =( ) A .2 B .1 C .0 D .-1 2.已知△ABC 的三边长分别是a ,b ,c ,有以下三个结论: (1)以a ,b ,c 为边长的三角形一定存在; (2)以a 2,b 2,c 2为边长的三角形一定存在; (3)以|a -b |+1,|b -c |+1,|c -a |+1为边长的三角形一定存在. 其中正确结论的个数为( ) A .0 B .1 C .2 D .3 3.若正整数a ,b ,c 满足a ≤b ≤c 且abc =2(a +b +c ),则称(a ,b ,c )为好数组.那么,好数组的个数为( ) A .1 B .2 C .3 D .4 4.设O 是四边形ABCD 的对角线AC ,BD 的交点,若∠BAD +∠ACB =180 ,且BC =3, AD =4,AC =5,AB =6,则DO OB =( ) A .109 B .87 C .65 D .43 5.设A 是以BC 为直径的圆上的一点,AD ⊥BC 于点D ,点E 在线段DC 上,点F 在CB 的延长线上,满足∠BAF =∠CAE .已知BC =15,BF =6,BD =3,则AE =( ) A .43 B .213 C .214 D .215 6.对于正整数n ,设a n 是最接近n 的整数,则1a 1+1a 2+1a 3+…+1a 200 =( ) A .1917 B .1927 C .1937 D .1947