
运筹学作业(第二章)
工商管理1班段振楠
1、习题2.8(第53页)
a、确定的活动和资源(如表一所示)
b、需要作出的决策:确定最佳投资比例,使得收益最大化。
决策的限制:6000美元的资金和600小时的时间
决策的全面绩效测度:600小时内最大的收益
c、定量表达式:总利润=投资A公司的利润*对A公司的投资比例+投资B公司的利润
*对B公司的投资比例
约束条件:对A公司投资+对B公司投资≤6000美元
对A公司投资时间+对B公司投资时间≤600小时
d、建立电子表格模型(如下图所示)
如图所示:表格中橙色为目标单元格,黄色为可变单元格,蓝色为数据单元格。
e、因为这个模型满足许多线性规划模型的特征:
1、需要做出许多活动水平的决策,因此可变单元格被用来显示这些水平。
2、这些活动的水平能够满足许多的约束条件的任何值
3、每个约束条件对活动水平的决策进行了限制
4、活动水平的决策是以进入目标单元格的一个完全绩效侧度为基准
5、每个输出单元格的Excel等式可表达为一个SUMPRODUCT函数。
f、建立代数模型如下:假设P为总利润,W为投资A公司的比例,D为投资B公司的比例。
目标函数为P=4500W+4500D
约束条件为5000W+4000D≤6000
400W+500D≤600
W≥0,D≥0
求得最优解为投资A公司资金、时间的三分之二,投资B公司资金、时间的三分之二,得最大总利润为6000美元。
h、图解法解答如下:
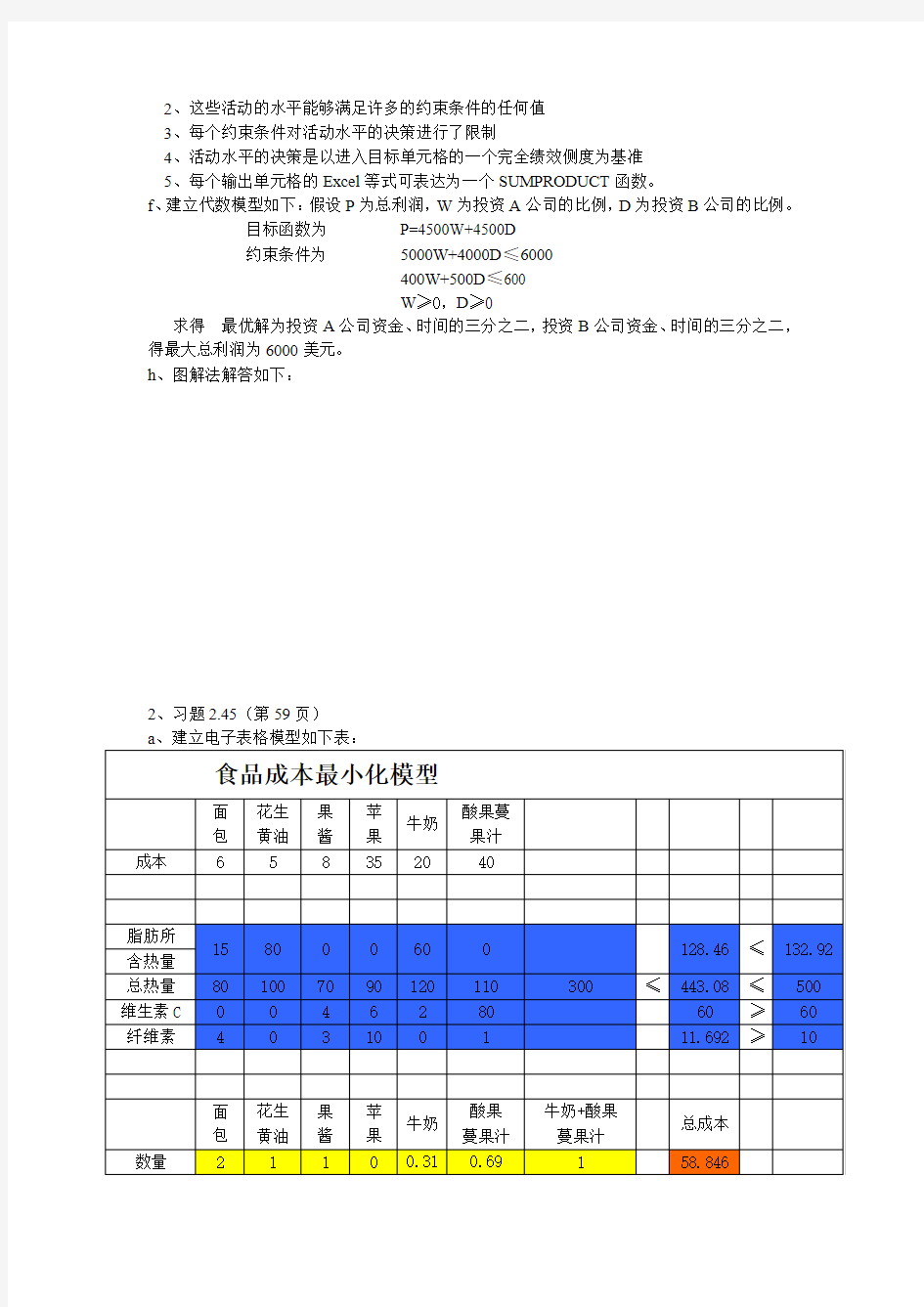
2、习题2.45(第59页)
由电子表格可知当食品构成为面包2片、花生黄油1汤匙、果酱1汤匙、牛奶0.31杯、果酸蔓果汁0.69杯时成本最小,为58.84美元
b、建立代数模型如下:(设P为总成本,A、B、C、D、E、F分别为面包、花生奶油、果酱、苹果、牛奶、果酸蔓果汁的用量)
依题意我们可知
目标函数为P=6A+5B+8C+35D+20E+40F
约束条件为A≥2, B≥1, C≥1, D≥0, E+F≥1
15A+80B+60E≤0.3*(80A+100B+70C+90D+120E+110F)
80A+100B+70C+90D+120E+110F≤500
80A+100B+70C+90D+120E+110F≥300
4C+6D+2E+80F≥60
4A+3C+10D+F≥10
3、习题3.4 (第88页)
a、要实现的目标是最后的现金余额最大,需要六年的现金流量,选择对项目A、B、C的投资比例,同时保证每年的资金余额大于等于100万。
b
若完全参加A
第一年的期末余额为
1000-400-0.5*1000+600=700万
第二年的期末余额为
700-600-0.5*350+600=350万
c、草拟的电子表格模型草图如下:
习题3.9(第89页)
1、选中“LT Loan”,从“工具”菜单中选择“审核/追踪从属单元格”,发现缺少了“LT Interest”的F16,它被错误的输入为“-0.47”,而没有按照计算公式“=LT Rate* LT Rate”计算。
2、选中“LT Payback”,从“工具”菜单中选择“审核/追踪引用单元格”,发现其出现了与“ST Loan”的E14相连的箭头,却缺少了与“LT Loan”相连的箭头。正确应为:LT Payback= LT Loan。
3、利用“工具”菜单中选择“审核/追踪引用单元格”,检查ST Interest的单元格G14,其多了受“LT Loan”影响的箭头,却缺少了受“ST Loan”影响的箭头。正确的是:G14= ST Rate*E13
习题4.6(第134页)
a、活动:比尔克公司的生产活动是希望在两台机器上生产三种零部件,并且确定三种零部件的最优组合,使得所得利润最大化。
资源:两台每周可生产40小时的机器,及零部件的材料。
b、建立电子表格模型如下:
c、进行3种猜想,由题意知,A零件的利润最大,B零件次之,C零件最小,所以猜想,最优解为全部生产A零件,最劣解为全部生产C零件。下面对猜想进行检验:
1.全部生产A零件:则40/0.02=2000(件),40/0.05=800(件),最大利润为
50*800=40000(美元)
2.全部生产B零件:则40/0.03=1333(件),40/0.02=2000(件),最大利润为
40*1333=53320(美元)
3.全部生产C零件:则40/0.05=800(件),40/0.04=1000(件),最大利润为
30*800=24000(美元)
由此可见,第二种收益最大,为53320美元.原猜想错误。
d、由电子表格模型可知:最优解为生产363.64个零部件A,生产1090.91个零部件B,不生产零部件C,总利润最大,为61818.18美元。
e、建立代数模型如下:
假设A、B、C分别为三种零件的生产量。则:
目标函数为P=50*A+40*B+30*C
约束条件为0.02*A+0.03*B+0.05*C≤40
0.05*A+0.02*B+0.04*C≤40
A≥0, B≥0, C≥0,
习题4.11(第135页)
a、在电子表格上建模如下:
b
将产生400单位的现金流,在第十年产生300单位的现金流、在第二十年产生550单位的现金流,总投入是400单位的现金。
c、猜想1:资产1 、资产2、资产3各投资100单位
则第五年、第十年、第二十年的现金流量分别为350单位、200单位、350
位.总投资为300单位.
猜想2: 资产1 、资产2、资产3各投资200单位
则第五年、第十年、第二十年的现金流量分别为700单位、400单位、700
位.总投资为600单位.
d、由Solver求得的最优解为投资资产一100单位、投资资产二200单位、不投资资产三,
总投入为300单位现金。
e、该问题的代数模型如下:
假设I为总投入,A为投资资产1的现金、B为投资资产2的现金、C为投资
资产3的现金。
目标函数为I=A+B+C
约束条件为2*A+B+0.5C≥400
0.5*A+0.5*B+C≥150
1.5*B+2C≥300
A≥0,B≥0,C≥0。
习题4.14(第136页)
a、此问题为成本收益平衡问题中的工程人员排程问题。因为该题通过线形规划以寻求最优
的成本收益的组合,即确定最佳的轮班人数组合。
利用solver求解得出最优解为总工资1728元,其中全职人员在各班次都是4人当班,兼职人员在各时段的安排人数依次为2人、0人、4人、2人。
c、建立代数模型如下
设P1、P2、P3、P4分别为兼职的人数,F1、F2、F3分别为全职的人数。则:目标函数为S=14*8*(F1+F2+F3)+12*4*(P1+P2+P3+P4)
约束条件为P1+F1≥6, P1+P2+F2≥8
P2+P3+F3≥12 P3+F4≥6
F1≥2*P1 F1+F2≥2*P2
F2+F3≥2*P3 F3≥2*P4
P1、P2、P3、P4、F1、F2、F3为非负
习题4.16(第136页)
a、需要确定的约束条件:
1、M1到S1的运输量最大为30吨
2、M1到S2的运输量最大为30吨
3、M2到S1的运输量最大为50吨
4、M2到S2的运输量最大为30吨
5、S1到P的运输量最大为70吨
6、S2到P的运输量最大为70吨
7、M1的开采量和运出量相等8、M2的开采量和运出量相等
9、P的需求量等于S1、S2的仓储量10、S1的仓储量等于运出量
11、S2的仓储量等于运出量
b
利用solver求解得:M1运到S1的数量是30吨,运到S2的数量是10吨;
M2运到S1的数量是10吨,运到S2的数量是50吨。
总成本是美元
c、为该问题建立代数模型如下:
设A为M1矿井到S1的运输量,B为M1矿井到S2的运输量;
C为M2矿井到S1的运输量,D为M2矿井到S2的运输量
E为S1矿井到P的运输量,F为S1矿井到P的运输量
则目标函数为 C=2000A+1700B+1600C+1100D+400E+800F
约束条件为 A≤30 B≤30 C≤50 D≤50 E≤70 F≤70
A+B=40 C+D=60 E+F=100
A+C=E B+D=F
习题4.24(第139页)
即目标函数C=4A+4B+7C+8D+15F+35E小
该问题的其他约束为:各种用料的用量非负。
b、为该问题建立电子表格模型如下:
利用solver求解得:应选用2.86片面包、0.74勺花生酱、一杯牛奶;最小成本为42.10美元。
c、为该问题建立代数模型如下:
设A、B、C、D、E、F依次为各原料的用料,则
目标函数为C=4A+4B+7C+8D+15F+35G
约束条件为X= 70A+100B+50C+60D+150F+100E≥400
70A+100B+50C+60D+150F+100E≤600
10A+75B+20D+70E≤0.3X
3C+2F+120E≥60
3A+4B+D+8F+E≥12
A、B、C、D、E、F≥0
5.6
a、最优解是:巧克力0加仑,香草300加仑香蕉75加仑
总利润为341.25美元
b、最优解变为:巧克力100加仑香草0加仑香蕉250加仑总利润为350美元
c、因为目标系数为0.95,增加上限为0.0214,降低下限为0.5,所以最优解的范围是0.9≤PB ≤0.9714,0.92在此范围内,所以最优解不变。总利润:300*0.90+0.92*75=339(美元)
d、奶油的影子价格为1美圆的有效范围:56.25≤奶油≤75,奶油57加仑在影子价格的有效范围内,因此,扔掉3加仑的奶油最优解改变。利润变为:341.25-3*1=311.25(美元)
e、糖的影子价格1.875美元的有效范围120≤糖≤160,165>160不在影子价格的有效范围内。当糖的供给量为160加仑时,总利润为:341.25+10*1.875=360美元,因为增加上限是10磅,所以会浪费5磅。
f、
影子价格:牛奶的需求量180小于可获得量200,所以,增加牛奶的可用量不会使总利润增加,因此影子价格为0。
增加上限:无限制。因为牛奶的影子价格为0,所以,无限增加牛奶的供给量,总利润
也不会改变,影子价格仍有效,由此得知.
降低下限:由影子价格和牛奶的需求量180小于可获得量200得知
习题5.10(第182页)
a、使用画图法解题如下:
b、增加1单位的求解如下:
c、电子表格模型求解如下:
求得最优解为投入1活动2单位的资源,投入2活动2单位的资源,利润为6美元。
d、运用solver分析得:
≤资源1≤12,
资源2的允许取值范围为3≤资源2≤8.
求得的影子价格是:资源1的影子价格:0.5元,资源2的影子价格:0.5元,在影子价格保持正确的前提下可用资源允许的范围是:
资源1: 4≤资源1≤12
资源2: 2.67≤资源2≤8
f、答:因为影子价格反应了约束常数增加微小量1,使得目标函数值增加的量。在影子价格的有效范围内变动约束常数,能使得目标函数值以一定的增量增加。当管理层在改变资源的可获得量时,其最关心的是,是否能改变目标函数值,使得利润更大。而影子价格直接关系到管理层所关心的目标函数值。在影子价格的有效范围内变动可获得的资源量,能使利润增长又不浪费资源。所以,影子价格是很有用的。
《运筹学》第三版(清华大学出版社)P79例1,表上作业法,运用西北角法确定初始基可行解。 西北角法是从西北角(左上角)格开始,在格内的右下角标上允许取得的最大数;然后按行(列)标下一格的数;若某行(列)的产量(销量)已满足,则把该行(列)的其他格划去;如此进行下去,直至得到一个基本可行解的方法。 西北角法的例子:P79例1 从表1中可知,总的产量=总的销量,故产销是平衡的。 第一步:列出运价表和调运物资平衡表。 运用表上作业法时,首先要列出被调运物资的运价表和供需平衡表(简称平衡表),如表1,2所示。 第二步:编制初始调运方案。 首先在表2的西北角方格(即左上角方格,对应变量x11),尽可能取最大值: x =min{3,7}=3 11 将数值3填入该方格(见表3)。由此可见x21,x31必须为0,即第一列其他各方格都不能取非零值,划去第一列。在剩下的方格中,找出其西北角方格x12,x =min{6,7-3}=4 12 将4填入它所对应方格,第一行饱和,划去该行。再找西北角方格x22, x =min{6-4,4}=2 22
将2填入x22所对应方格,于是第二列饱和,划去该列。继续寻找西北方格为x23, x =min{5,4-2}=2 23 将2填入x23所对应方格,第二行饱和,划去该行。剩下方格的西北角方格为x33, x 3=min{5-2,9}=3 3 将3填入x33所对应方格,第三列饱和,划去该列。最后剩下x34方格,取x34 = 6。 这样我们就找到了m+n-1=3+5-1=7个基变量,它们为:x11= 3,x12= 4,x22 = 2,x23 = 2,x33 = 3,x34 = 6。显然它们用折线连接后不形成闭回路。这就是西北角法所找初始基可行解,所对应的目标值为: 2×200+1×250+3×150+1×150+3×250+3×300+4×200=4000 我们找到的初始基可行解可通过各行方格中数值之和是否等于产量,各列方格中数值之和是否等于销量来简单验证。 利用西北角法找初始基可行解简单可行,但也存在问题。例如在表3中可见c = 4,单价高于该行其他各方格,最简单想法是单价小的情况下多运些货物,35 这样总运费会更小些,最小元素法就改进了西北角法的缺点。
第一章线性规划1、 由图可得:最优解为 2、用图解法求解线性规划: Min z=2x1+x2 ? ? ? ? ? ? ? ≥ ≤ ≤ ≥ + ≤ + - 10 5 8 24 4 2 1 2 1 2 1 x x x x x x 解: 由图可得:最优解x=1.6,y=6.4
Max z=5x 1+6x 2 ? ?? ??≥≤+-≥-0 ,23222212 121x x x x x x 解: 由图可得:最优解Max z=5x 1+6x 2, Max z= +∞
Maxz = 2x 1 +x 2 ????? ? ?≥≤+≤+≤0,5242261552121211x x x x x x x 由图可得:最大值?????==+35121x x x , 所以?????==2 3 21x x max Z = 8.
12 12125.max 2328416412 0,1,2maxZ .j Z x x x x x x x j =+?+≤? ≤?? ≤??≥=?如图所示,在(4,2)这一点达到最大值为2 6将线性规划模型化成标准形式: Min z=x 1-2x 2+3x 3 ????? ??≥≥-=++-≥+-≤++无约束 321 321321321,0,05232 7x x x x x x x x x x x x 解:令Z ’=-Z,引进松弛变量x 4≥0,引入剩余变量x 5≥0,并令x 3=x 3’-x 3’’,其中 x 3’≥0,x 3’’≥0 Max z ’=-x 1+2x 2-3x 3’+3x 3’’ ????? ? ?≥≥≥≥≥≥-=++-=--+-=+-++0 ,0,0'',0',0,05 232 '''7'''543321 3215332143321x x x x x x x x x x x x x x x x x x x
《运筹学》作业 第2章 1.某公司计划生产两种产品,已知生产单位产品所需的三种原材料的消耗及所获的利润,如下表所示。问应如何安排生产使该工厂获利最多?(建立模型,并用图解法求解) 答:产品1和产品2分别生产15和7.5单位,最大利润是975. 2.某公司计划生产两种产品,已知生产单位产品所需的两种原材料的消耗和人员需要及所获的利润,如下表所示。问应如何安排生产使该工厂获利最多?(建立模型,并用图解法求解) 答:产品1和产品2分别生产2和6单位,最大利润是3600. 3. 下表是一个线性规划模型的敏感性报告,根据其结果,回答下列问题: 1)是否愿意付出11元的加班费,让工人加班; 2)如果第二种家具的单位利润增加5元,生产计划如何变化? Microsoft Excel 9.0 敏感性报告 工作表 [ex2-6.xls]Sheet1 报告的建立: 2001-8-6 11:04:02 可变单元 格 终递减目标式允许的允许的单元格名字值成本系数增量减量 $B$15 日产量(件)100 20 60 1E+30 20 $C$15 日产量(件)80 0 20 10 2.5 $D$15 日产量(件)40 0 40 20 5.0 $E$15 日产量(件)0 -2.0 30 2.0 1E+30 约束 终阴影约束允许的允许的单元格名字值价格限制值增量减量 $G$6 劳动时间(小时/件)400 8 400 25 100 $G$7 木材(单位/件)600 4 600 200 50
$G$8 玻璃(单位/件)800 0 1000 1E+30 200 答:1)因为劳动时间的阴影价格是8,所以不会愿意付出11元的加班费,让工人加班;2)因为允许的增加量是10,所以生产计划不变。 4某公司计划生产两种产品,已知生产单位产品所需的三种原材料的消耗及所获的利润,如 5. 下表是一个线性规划模型的敏感性报告,根据其结果,回答下列问题: 1)是否愿意付出11元的加班费,让工人加班; 2)如果工人的劳动时间变为402小时,日利润怎样变化? 3)如果第二种家具的单位利润增加5元,生产计划如何变化? Microsoft Excel 9.0 敏感性报告 工作表 [ex2-6.xls]Sheet1 报告的建立: 2001-8-6 11:04:02 可变单元 格 终递减目标式允许的允许的单元格名字值成本系数增量减量 $B$15 日产量(件)100 20 60 1E+30 20 $C$15 日产量(件)80 0 20 10 2.5 $D$15 日产量(件)40 0 40 20 5.0 $E$15 日产量(件)0 -2.0 30 2.0 1E+30 约束 终阴影约束允许的允许的单元格名字值价格限制值增量减量 $G$6 劳动时间(小时/件)400 8 400 25 100 $G$7 木材(单位/件)600 4 600 200 50 $G$8 玻璃(单位/件)800 0 1000 1E+30 200 答:1)因为劳动时间的阴影价格是8,所以不会愿意付出11元的加班费,让工人加班;2)日利润增加2*8=16 3)因为允许的增加量是10,所以生产计划不变。 第3章 1.一公司开发出一种新产品,希望通过广告推向市场。它准备用电视、报刊两种广告形式。 这两种广告的情况见下表。要求至少30万人看到广告,要求电视广告数不少于8个,
大连科技学院运筹学(Z)大作业LINGO软件在函数最大值中的运用 学院名称 专业班级 学生组号 学生姓名 指导教师 二〇一八年五月
实验LINGO软件在函数最大值中的运用 大作业目的 掌握LINGO软件求解函数最大值的基本步骤,了解LINGO软件解决函数最大值的基本原理,熟悉常用的函数最大值计算代码,理解函数最大值的迭代关系。 仪器、设备或软件 电脑,LINGO软件 大作业内容 1.LINGO软件求解函数最大值的基本原理; 2.编写并调试LINGO软件求解函数最大值的计算代码; 实施步骤 1.使用LINGO计算并求解函数最大值问题; 2.写出实验报告,并浅谈学习心得体会(选址问题的基本求解思路与方法及求解过程中出现的问题及解决方法)。 实施过程 有一艘货轮,分为前、中、后三个舱位,它们的容积与允许载重量如下表所示。现有三种商品待运,已知有关数据列于下表中。又为了航运安全,要求前、中、后舱在实际载重量上大体保持各舱最大允许载重量的比例关系。具体要求前、后舱分别与中舱之间的载重量比例偏差不超过15%,前、后舱之间不超过10%。问货轮应装载A、B、C各多少件,运费收入为最大?试建立这个问题的线性规 首先分析问题,建立数学模型: 确定决策变量 假设i=1,2,3分别代表商品A、B、C,8用j=1,2,3分别代表前、中、后舱,设决策变量x ij为装于j舱位的第i种商品的数量(件)。 确定目标函数
商品A 的件数为: 商品B 的件数为: 商品A 的件数为: 为使运费最高,目标函数为: 确定约束条件 前、中、后舱位载重限制为: 前、中、后舱位体积限制为: A 、 B 、 C 三种商品数量的限制条件: 各舱最大允许载重量的比例关系构成的约束条件: 且决策变量要求非负,即x ij ≥0,i=1,2,3;j=1,2,3。 综上所述,此问题的线性规划数学模型为: 111213x x x ++212223x x x ++313233x x x ++()()()111213212223313233 1000700600Max Z x x x x x x x x x =++++++++112131122232132333865200086530008651500 x x x x x x x x x ++≤++≤++≤112131122232132333105740001057540010571500 x x x x x x x x x ++≤++≤++≤1112132122233132336001000800 x x x x x x x x x ++≤++≤++≤1121311222321323331222321121311323338x 6x 5x 2 2(10.15)(1+0.15)38x 6x 5x 3 8x 6x 5x 11(10.15)(1+0.15)28x 6x 5x 2 8x 6x 5x 4 4(10.10)(1+0.10)38x 6x 5x 3++-≤≤++++-≤≤++++-≤≤++()()() 111213212223313233112131122232132333112131122232132333 1000700600865200086530008651500105740001057540010571500 Max Z x x x x x x x x x x x x x x x x x x x x x x x x x x x =++++++++++≤++≤++≤++≤++≤++≤
线性规划建模及单纯形法 思考题 主要概念及内容: 线性规划模型结构(决策变量,约束不等式、等式,目标函数);线性规划标准形式; 可行解、可行集(可行域、约束集),最优解;基、基变量、非基变量、基向量、非基 向量;基本解、基本可行解、可行基、最优基。 复习思考题: 1、线性规划问题的一般形式有何特征? 2、建立一个实际问题的数学模型一般要几步? 3、两个变量的线性规划问题的图解法的一般步骤是什么? 4、求解线性规划问题时可能出现几种结果,哪种结果反映建模时有错误? 5、什么是线性规划的标准型,如何把一个非标准形式的线性规划问题转化成标准形式。 6、试述线性规划问题的可行解、基本解、基本可行解、最优解、最优基本解的概念及它 们之间的相互关系。 7、试述单纯形法的计算步骤,如何在单纯形表上判别问题具有唯一最优解、有无穷多个 最优解、无界解或无可行解。 8、在什么样的情况下采用人工变量法,人工变量法包括哪两种解法? 9、大M 法中,M 的作用是什么?对最小化问题,在目标函数中人工变量的系数取什 么?最大化问题呢? 10、什么是单纯形法的两阶段法?两阶段法的第一段是为了解决什么问题?在怎样的情 况下,继续第二阶段? 作业习题 1、将下列线性规划问题化为标准型 (1)???????≥=--+-≥-+-≤+-++-+=0,,953413223183622453max 4214321432143214321x x x x x x x x x x x x x x x x x x x z (2)???????≤≥=+-+-≥-+--≤--++++=0 ,0,15 2342722351232243min 4214321432143214 321x x x x x x x x x x x x x x x x x x x f 2、(1)求出下列不等式组所定义的多面体的所有基本解和基本可行解(极点): ?????≥≤++-≤++0,,1243263323 21321321x x x x x x x x x (2)对下述线性规划问题找出所有基本解,指出哪些是基本可行解,并确定最优解. ??? ????≥=-=+-+=+++++=)6,,1(00 31024893631223max 61532143213 21K K j x x x x x x x x x x x x x x z j 3、用图解法求解下列线性规划问题
<运筹学>课后答案 [2002年版新教材] 前言: 1、自考运筹学课后作业答案,主要由源头活水整理;gg2004、杀手、mummy、promise、月影骑士、fyb821等同学作了少量补充。 2、由于水平有限,容如果不对之处,敬请指正。欢迎大家共同学习,共同进步。 3、帮助别人,也是帮助自己,欢迎大家来到易自考运筹学版块解疑答惑。 第一章导论P5 1.、区别决策中的定性分析和定量分析,试举例。 定性——经验或单凭个人的判断就可解决时,定性方法 定量——对需要解决的问题没有经验时;或者是如此重要而复杂,以致需要全面分析(如果涉及到大量的金钱或复杂的变量组)时,或者发生的问题可能是重复的和简单的,用计量过程可以节约企业的领导时间时,对这类情况就要使用这种方法。 举例:免了吧。。。 2、. 构成运筹学的科学方法论的六个步骤是哪些? .观察待决策问题所处的环境; .分析和定义待决策的问题; .拟定模型; .选择输入资料; .提出解并验证它的合理性(注意敏感度试验); .实施最优解; 3、.运筹学定义: 利用计划方法和有关许多学科的要求,把复杂功能关系表示成数学模型,其目的是通过定量分析为决策和揭露新问题提供数量根据 第二章作业预测P25 1、. 为了对商品的价格作出较正确的预测,为什么必须做到定量与定性预测的结合?即使在定量预测法诸如加权移动平均数法、指数平滑预测法中,关于权数以及平滑系数的确定,是否也带有定性的成分? 答:(1)定量预测常常为决策提供了坚实的基础,使决策者能够做到心中有数。但单靠定量预测有时会导致偏差,因为市场千变万化,影响价格的因素很多,有些因素难以预料。调查研究也会有相对局限性,原始数据不一定充分,所用的模型也往往过于简化,所以还需要定性预测,在缺少数据或社会经济环境发生剧烈变化时,就只能用定性预测了。(2)加权移动平均数法中权数的确定有定性的成分;指数平滑预测中的平滑系数的确定有定性的成分。 2.、某地区积累了5 个年度的大米销售量的实际值(见下表),试用指数平滑法,取平滑
No .1 线性规划 1、某织带厂生产A 、B 两种纱线和C 、D 两种纱带,纱带由专门纱线加工而成。 工厂有供纺纱的总工时7200h ,织带的总工时1200h 。 (1) 列出线性规划模型,以便确定产品的数量使总利润最大; (2) 如果组织这次生产具有一次性的投入20万元,模型有什么变化?对模型的 解是否有影响?(所谓一次性投入就是与产量无关的初始投资) 2、将下列线性规划化为极大化的标准形式 3、用单纯形法解下面的线性规划 ??? ??? ?≥≤++-≤++-≤-+++= ,0,,4205.021********* ..352)(m ax 3213213213213 21x x x x x x x x x x x x t s x x x x f No .2 两阶段法和大M 法 2、用大M 法解下面问题,并讨论问题的解。 ??? ??? ?≥≥++≤++-≤++++= ,0,,52151565935 ..121510)(max 3213213213213 21x x x x x x x x x x x x t s x x x x f 1、用两阶段法解下面问题: ??? ??≥≥+≥++=0,75 3802 ..64)(min 2 121212 1x x x x x x t s x x x f ?????? ?±≥≤+-=-+--≥-+++=不限 321321321321321 ,0,13|5719|169765 ..532)(m in x x x x x x x x x x x x t s x x x x f
No .3 线性规划的对偶问题 ?????-≤≤-≤≤≤≤-+-=8121446 2 ..834)(min 3213 21x x x t s x x x x f 2、写出下问题的对偶问题,解对偶问题,并证明原问题无可行解 3、用对偶单纯形法求下面问题 ??? ??≥≥+≥++=0,75 3802 ..64)(min 2 121212 1x x x x x x t s x x x f No .4 线性规划的灵敏度分析 原问题为max 型,x 4,x 5为松驰变量,x 6为剩余变量,回答下列问题: (1)资源1、2、3的边际值各是多少?(x 4,x 5是资源1、2的松驰变量,x 6是资 源3的剩余变量) (2)求C 1, C 2 和C 3的灵敏度范围; (3)求?b 1,?b 2的灵敏度范围。 1、写出下列线性规划问题的对偶问题: (1) ???????±≥≤=++≤+≥+-+-+=不限 432143231 4321321 ,0,,06 4 2 5 ..532)(max x x x x x x x x x x x x x t s x x x x f (2) ?????? ?≥≤+--≤-≤+--= ,0, 121 1 ..34)(m ax 212122121x x x x x x x t s x x x f
运筹学(胡运权)第五版课后答案-运筹作业
47页1.1b 用图解法找不到满足所有约束条件的公共范围,所以该问题无可行解47页1.1d 无界解 1 2 3 4 5 4 3 2 1 - 1 -6 -5 -4 -3 -2 X2 X1 2x1- -2x1+3x 1 2 3 4 4 3 2 1 X1 2x1+x2=2 3x1+4x2= X
1.2(b) 约束方程的系数矩阵A= 1 2 3 4 2 1 1 2 P1 P2 P3 P4 基 基解 是否可行解目标函数值X1 X2 X3 X4 P1 P2 -4 11/2 0 0 否 P1 P3 2/5 0 11/5 0 是43/5 P1 P4 -1/3 0 0 11/6 否 P2 P3 0 1/2 2 0 是 5 P2 P4 0 -1/2 0 2 否 P3 P4 0 0 1 1 是 5 最优解A=(0 1/2 2 0)T和(0 0 1 1)T 49页13题 设Xij为第i月租j个月的面积 minz=2800x11+2800x21+2800x31+2800x41+4500x12+4500x22+4500x32+6000x1 3 +6000x23+7300x14 s.t. x11+x12+x13+x14≥15 x12+x13+x14+x21+x22+x23≥10 x13+x14+x22+x23+x31+x32≥20 x14+x23+x32+x41≥12 Xij≥0 用excel求解为: ( )
用LINDO求解: LP OPTIMUM FOUND AT STEP 3 OBJECTIVE FUNCTION V ALUE
哈工大运筹学大作业-对偶 单纯形法对比 标准化文件发布号:(9312-EUATWW-MWUB-WUNN-INNUL-DQQTY-
运筹学课程 运筹学对偶单纯形法与单纯形法 对比分析大作业 哈尔滨工业大学工业工程系 学生姓名: 学号: 指导教师: 成绩: 评语:
运筹学对偶单纯形法与单纯形法对比分析 摘要:这篇论文主要介绍了对偶单纯形法的实质、原理、流程和适用条件等。将对偶单纯形法与单纯形法的基本思想进行对比分析,从而说明对偶单纯形法的优点和适用范围。 关键词:对偶单纯形法;对偶理论;单纯形法;基本思想 在线性规划早期发展阶段的众多重要发现中,对偶的概念及其分支是其中最重要的内容之一。这个发现指出,对于任何一个线性规划问题都具有对应的称为对偶问题的线性规划问题。对偶问题与原问题的关系在众多领域都非常有用。 (一)教学目标: 通过对偶单纯形法的学习,加深对对偶问题的理解。掌握对偶单纯形法的解题过程,理解对偶理论的其原理,了解对偶单纯形法的作用和应用范围 (二)教学内容: 1)对偶单纯形法的思想来源 2)对偶单纯形法原理 3)对偶理论的实质 4)单纯形法和对偶单纯形法的比较 (三)教学进程: 一、对偶单纯形法的思想来源
所谓对偶单纯形法,就是将单纯形法应用于对偶问题的计算,该方法是由美国数学家C.莱姆基于1954 年提出的,它并不是求解对偶问题解的方法,而是利用对偶理论求解原问题的解的方法。 二、对偶问题的实质 下面是原问题的标准形式以及其对应的对偶问题: 原问题对偶问题 从而可以发现如下规律: 1.原问题目标函数系数是对偶问题约束方程的右端项。 2.原问题约束方程的右端项是对偶问题目标函数的系数。 3.原问题一个变量在所有约束方程中的系数是对偶问题一个约束方程中的所有系数。 三、对偶单纯形法原理 对偶单纯形法是通过寻找原问题的对偶问题的可行解来求解原问题的最优解的方法,它的应用包括影子价格和灵敏度分析等。为了理解对偶单纯形法为什么能够解出原方程的最优解,我们需要对对偶理论的几个基本原理有所了解。 1.弱对偶性 如果是原问题的可行解,是其对偶问题的可行解,则恒有
第一章 第一章 1. 建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。决策变量(Decision Variable)是决策问题待定的量值,取值一般为非负;约束条件(Constraint Conditions)是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数(Objective Function)是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。 2.(1)设立决策变量; (2)确定极值化的单一线性目标函数; (3)线性的约束条件:考虑到能力制约,保证能力需求量不能突破有效供给量; (4)非负约束。 3.(1)唯一最优解:只有一个最优点 (2)多重最优解:无穷多个最优解 (3)无界解:可行域无界,目标值无限增大 (4)没有可行解:线性规划问题的可行域是空集 无界解和没有可行解时,可能是建模时有错。 4. 线性规划的标准形式为:目标函数极大化,约束条件为等式,右端常数项bi≥0 , 决策变量满足非负性。 如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。 5. 可行解:满足约束条件AX =b,X≥0的解,称为可行解。 基可行解:满足非负性约束的基解,称为基可行解。 可行基:对应于基可行解的基,称为可行基。 最优解:使目标函数最优的可行解,称为最优解。 最优基:最优解对应的基矩阵,称为最优基。 6. 计算步骤: 第一步,确定初始基可行解。 第二步,最优性检验与解的判别。 第三步,进行基变换。 第四步,进行函数迭代。 判断方式: 唯一最优解:所有非基变量的检验数为负数,即σj< 0 无穷多最优解:若所有非基变量的检验数σj≤ 0 ,且存在某个非基变量xNk 的检验数σk= 0 ,让其进基,目标函数的值仍然保持原值。如果同时存在最小θ值,说明有离基变量,则该问题在两个顶点上同时达到最优,为无穷多最优解。无界解:若某个非基变量xNk 的检验数σk> 0 ,但其对应的系数列向量P k' 中,每一个元素a ik' (i=1,2,3,…,m)均非正数,即有进基变量但找不到离基变量。
运筹学课程设计报告书 专业 班级 学号 姓名LMZZ 日期2011.09.01
设计题目:运输问题的表上作业法 设计方案:运输问题是一种应用广泛的网络最优化模型,该问题的主要目的是为物资调运、车辆高度选择最经济的运输路线。有些问题,如m 台机床加工零件问题、工厂合理布局问题,虽要求与提法不同,经适当变化也可以使用本模型求得最佳方案。 运输问题的一般提法: 某种物资有m 个产地Ai ,产量是ai (i =1,2,…,m ),有m 个销售地Bi ,销量(需求量)是bj(j=1,2,…,m)。若从Ai 运到Bi 单位运价为dij(i=1,2,…,m;j=1,2,…,m),又假设产销平衡,即 ∑∑===m i n j j i b a 11 问如何安排运输可使总运费最小? 若用x ij (i=1,2,…,m;j=1,2,…,n)表示由A i 运到B j 的运输量,则平衡运输问题可写出以下线性规划模型:
∑∑===m i n j ij ij x d Z 11min 约束条件 ?????????==≥====∑∑==) ,...,2,1;...,2,1(0)...,2,1()...,2,1(11n j m i x n j b x m i a x ij m i j ij n j i ij 表上作业法原理同于单纯形法,首先给出一个初始的调运方案(实际上是初始基本可行解),求出各非基变量的检验数去判定当前解是否为最优解,若不是则进行方案调整(即从一个基本可行解转换成另一个基本可行解),再判定是否为最优解,重复以上步骤,直到获得最优解为止。这些步骤在表上进行十分方便。 操作过程在表上进行 方案实施:通过运输问题在C++程序中的运用,从而实现方案的最优。程序主要分两部:(1)求解,(2)最优解判断 结果与结论:程序运行过程中,依次输入所需要的运价,产量,销量等数据,单击回车可以再次现实所需数据,按任意键可以运行至求出初始可行解并显示,再次按任意键程序进行最优解的判断,并求出最优解,显示在程序页面上,从而可以得到该运输问题的最优方案。
管理运筹学作业答案MBA
第1章 线性规划基本性质 P47 1—1(2) 解:设每天从i 煤矿()2,1=i 运往j 城市()3,2,1=j 的煤为ij x 吨,该问题的LP 模型为: () ?????????? ?==≥=+=+=+=++=+++++++==∑∑==3,2,1;2,10200150100250 200 ..85.681079min 231322122111232221 13121123 22211312112 13 1j i x x x x x x x x x x x x x t s x x x x x x x c ij i j ij ij ω P48 1—2(2) ??? ??≥-≤-≥-+=0,)2(33) 1(0..max 2 1212121x x x x x x t s x x z
解:Φ =2 1 R R ,则该LP 问题无可行解。 P48 1—2(3) ??? ??≥-≥-≥--=0,)2(55)1(0..102min 2 1212121x x x x x x t s x x z
解:目标函数等值线与函数约束(2)的边界线平行,由图可知则该LP 问题为多重解(无穷多最优解)。 ?? ?? ?==????-=-=-45 45550212121x x x x x x 则10 ,45,45**1-=?? ? ??=z X T (射线QP 上所有点均为最优点) P48 1—2(4) ???????≥≤-≤+≤+--=0 ,)3(22)2(825) 1(1043..1110min 212121 2121x x x x x x x x t s x x z
课程名称:对偶单纯形法 一、教学目标 在对偶单纯形法的学习过程中,理解和掌握对偶问题;综合运用线性规划和对偶原理知识对对偶单纯形法与单纯形法进行对比分析,了解单纯形法和对偶单纯形法的相同点和不同点,总结出各自的适用范围;掌握对偶单纯形法的求解过程;并能运用对偶单纯形法独立解决一些运筹学问题。 二、教学内容 1) 对偶单纯形法的思想来源(5min) 2) 对偶单纯形法原理(5min) 3) 总结对偶单纯形法的优点及适用情况(5min) 4) 对偶单纯形法的求解过程(10min) 5) 对偶单纯形法例题(15min) 6) 对比分析单纯形法和对偶单纯形法(10min) 三、教学进程: 1)讲述对偶单纯形法思想的来源: 1954年美国数学家C.莱姆基提出对偶单纯形法(Dual Simplex Method )。单纯形法是从原始问题的一个可行解通过迭代转到另一个可行解,直到检验数满足最优性条件为止。对偶单纯形法则是从满足对偶可行性条件出发通过迭代逐步搜索原始问题的最优解。在迭代过程中始终保持基解的对偶可行性,而使不可行性逐步消失。因此在保持对偶可行性的前提下,一当基解成为可行解时,便也就是最优解。 2)讲述对偶单纯形法的原理 A.对偶问题的基本性质 依照书第58页,我们先介绍一下对偶问题的六个基本性质: 性质一:弱对偶性 性质二:最优性。如果 x j (j=1...n)原问题的可行解,y j 是其对偶问题可 行解,且有 ∑=n j j j x c 1 =∑=m i i i y b 1 ,则x j 是原问题的最优解,y j 是其对偶问题的最
优解。 性质三:无界性。如果原问题(对偶问题)具有无界解,则其对偶问题(原问题)无可行解。 性质四:强对偶性。如果原问题有最优解,则其对偶问题也一定有最优解。 性质五:互补松弛型。在线性规划问题的最优解中,如果对应某一约束条件的对偶变量值为零,则该约束条件取严格等式;反之如果约束条件取严格不等式,则其对应的对偶变量一定为零。 性质六:线性规划的原问题及其对偶问题之间存在一对互补的基解,其中原问题的松弛变量对应对偶问题的变量,对偶问题的剩余变量对应原问题的变量;这些互相对应的变量如果在一个问题的解中是基变量,则在另一问题的解中是非基变量;将这对互补的基解分别代入原问题和对偶问题的目标函数有z=w. B.对偶单纯形法(参考书p64页) 设某标准形式的线性规划问题,对偶单纯形表中必须有c j -z j ≤0(j=1...n),但b i (i=1...m)的值不一定为正,当对i=1...m ,都有b i ≥0时,表中原问题和对偶问题均为最优解,否则通过变换一个基变量,找出原问题的一个目标函数值较小的相邻的基解。 3)为什么要引入对偶单纯形法 从理论上说原始单纯形法可以解决一切线性规划问题,然而实际问题中,由于考虑问题的角度不同,变量设置的不同,便产生了原问题及其对偶问题,对偶问题是原问题从另外一个角度考虑的结果。用对偶单纯形法求解线性规划问题时,当约束条件为“≥”时,不必引入人工变量,使计算简化。 例如,有一线性规划问题: min ω =12 y 1 +16y 2 +15 y 3 约束条件 ?? ?? ???≥=≥+≥+0)3,2,1(3522 423121 i y y y y y i
第一章习题 1.思考题 (1)微分学求极值的方法为什么不适用于线性规划的求解? (2)线性规划的标准形有哪些限制?如何把一般的线性规划化为标准形式? (3)图解法主要步骤是什么?从中可以看出线性规划最优解有那些特点? (4)什么是线性规划的可行解,基本解,基可行解?引入基本解和基可行解有什么作用? (5)对于任意基可行解,为什么必须把目标函数用非基变量表示出来?什么是检验数?它有什么作用?如何计算检验数? (6)确定换出变量的法则是什么?违背这一法则,会发生什么问题? (7)如何进行换基迭代运算? (8)大M法与两阶段法的要点是什么?两者有什么共同点?有什么区别? (9)松弛变量与人工变量有什么区别?试从定义和处理方式两方面分析。 (10)如何判定线性规划有唯一最优解,无穷多最优解和无最优解?为什么? 2.建立下列问题的线性规划模型: (1)某厂生产A,B,C三种产品,每件产品消耗的原料和设备台时如表1-18所示: 润最大的模型。 (2)某公司打算利用具有下列成分(见表1-19)的合金配制一种新型合金100公斤,新合金含铅,锌,锡的比例为3:2:5。 如何安排配方,使成本最低? (3)某医院每天各时间段至少需要配备护理人员数量见表1-20。
表1-20 假定每人上班后连续工作8小时,试建立使总人数最少的计划安排模型。能否利用初等数学的视察法,求出它的最优解? (4)某工地需要30套三角架,其结构尺寸如图1-6所示。仓库现有长6.5米的钢材。如何下料,使消耗的钢材最少? 图1-6 3. 用图解法求下列线性规划的最优解: ?????? ?≥≤+-≥+≥++=0 ,425.134 1 2 64 min )1(21212 12121x x x x x x x x x x z ?????? ?≥≤+≥+-≤++=0 ,82 5 1032 44 max )2(21212 12121x x x x x x x x x x z ????? ????≥≤≤-≤+-≤++=0 ,6 054 4 22232 96 max )3(2122 1212121x x x x x x x x x x x z ??? ??≥≤+-≥+ +=0,1 12 34 3 max )4(2 12 12121x x x x x x x x z
人力资源分配问题 第一题 (1)安排如下: x1=8,x2=0,x3=1,x4=1,x5=0,x6=4,x7=0,x8=6,x9=0x10=0,x11=0。 (2)总额为320,一共需安排20个班次; 因为在13:00—14:00,14:00—15:00,16:00—17:00,分别存在2,9,5个工时的剩余,(例如11:00—12:00)安排了8个员工而在14:00-15:00剩余了九个所以可以安排一些临时工工作3个小时的班次,使得总成本更小。 (3)在18:00—19:00安排6个人工作4小时;在11:00—12:00安排8个人,13:00—14:00安排1个人,15:00—16:00安排1个人,17:00—18:00安排4个人工作3小时。总成本最低为264元。
生产计划优化问题第二题 产品1在A 1生产数量为1200单位,在A 2 上生产数量为230单位,在B 1 上不生产,B 2 上生产数量为 858单位,B 3 上生产数量为571单位;产品2在A1上不生产,在A2上生产数量为500单位,在B1上生产数量为500单位;产品3在A2上生产数量为324单位,在B2上生产数量为324单位。最大利润为2293.29元。
第三题 设Xi为产品i最佳生产量。 (1)最优生产方案唯一,为X1=1000、X2=1000、X3=1000、X4=1000、X5=1000、X6=55625、X7=1000. (2)如上图所示,产品5的单价价格为0-30时,现行生产方案保持最优。 (3)由于环织机工的影子价格为300,且剩余变量值为零,而其他几种资源的影子价格为0,剩余变量均大于0,所以应优先增加环织工时这种资源的限额,能增加3.33工时,单位费用应低于其影子价格300才是合算的。 (4)因为产品2对偶价格= -3.2<0 ,950>933.33,3.2*(1000-950)=160;所以当产品2的最低销量从1000减少到950时,总利润增加160元。 (5)原最优解并没有把针织工时用尽,还有943.75工时的剩余,因此,不能通过增加针织工时来提高总利润。 (6)环织工时为630 - 5003.33时,最优生产方案不变,因为5010>5003.33,因此,若环织机工时的限额提高到5010小时,最优生产方案发生了变化。
浙江大学远程教育学院 《运筹学》课程作业 姓名:姜胜超学号:715003322021 年级:15秋学习中心:宁波学习中心————————————————————————————— 第2章 1.某公司计划生产两种产品,已知生产单位产品所需的三种原材料的消耗及所获的利润, 产品1 产品2 可用的材料数 原材料A 原材料B 原材料C 1 3 2 2 2 30 60 24 单位产品获利40万元50万元 1. 产品利润为P(万元) 则P=40x+50y 作出上述不等式组表示的平面区域,即可行域:
由约束条件可知0ABCD 所在的阴影部分,即为可行域 目标函数P=40x+50y 是以P 为参数,-54 为斜率的一族平行线 y =- 5 4 x +50P (图中红色虚线) 由上图可知,目标函数在经过C 点的时候总利润P 最大 即当目标函数与可行域交与C 点时,函数值最大 即最优解C=(15,7.5),最优值P=40*15+50*7.5=975(万元) 答:当公司安排生产产品1为15件,产品2为7.5件时使工厂获利最大。 2. 某公司计划生产两种产品,已知生产单位产品所需的两种原材料的消耗和人员需要及所 获的利润,如下表所示。问应如何安排生产使该工厂获利最多?(建立模型,并用图解 产品1 产品2 可用的材料数 原材料A 原材料B 人时 1 0 3 0 2 2 4 12 24 单位产品获利 300万元 500万元 解:设生产产品1为x 件,生产产品2为y 件时,使工厂获利最多 产品利润为P (万元) 则 P=300x+500y 作出上述不等式组表示的平面区域,即可行域:
运筹学课程上机实践要求及内容(2) 一、实验教学的目的和要求 目的:借助运筹学软件的强大功能,通过小组的充分讨论,对管理实践中的实际问题进行建模、求解,并对求解结果进行分析(特别是敏感性分析),进而激发学生的学习兴趣和热情,克服对课程学习的“恐惧感”。 要求:熟练掌握LINGO、WinQSB等软件的基本功能和基本语法结构,能用软件对运筹学问题进行求解和分析。 二、请于第1次-第6次上机时间及平时完成。 三、作业务请写清学号、姓名、专业、班级,上机作业格式请用老 师提供的模版。 四、编写的代码请用记事本单独保存。 五、要求所有题目用LINGO和教材自带的求解软件各做一遍。并分 析解释求解的结果。 六、各题目中的A,B,C,D,E,F为参数,除特别规定外,请自 行设定,各个同学参数值不能相同,若发现完全一致的,作业以零分计。 A=1,B=2,C=2,D=4,E=4,F=1
第1题(线性规划) (1)介绍单纯型算法及其处理人工变量的两阶段法; (2)建立下列问题的数学模型并求解,讨论资源的影子价格; 某造纸厂拟生产漂白松木浆、包装纸(水泥、松木包装纸、松木本色纸)、漂白桦木纸和胶版纸等四种产品,单位产品所需资源情况见表1,市场上胶版纸的需求量不超过6000吨。(a)制订该造纸厂的生产计划;(b)若电的资源可用量下降10%,重新制订该造纸厂的生产计划。 (3)结合本题,谈谈你对线性规划的认识。 Hint: 若参数为5,5,5,5,5,5,则最优目标函数值为(a)167236800; (b)167236800。 解: (1)单纯形法是求解线性规划问题的通用方法。单纯形法的基本思想是:先找出 一个基本可行解,对它进行鉴别,看是否是最优解;若不是,则按照一定法则转 换到另一改进的基本可行解,再鉴别;若仍不是,则再转换,按此重复进行。因 基本可行解的个数有限,故经有限次转换必能得出问题的最优解。如果问题无最 优解也可用此法判别。 两阶段单纯形法也是一种人工变量法,它的算法可分为两个阶段:第一阶段,引 入人工变量,构造一个具有标准基的新线性规划,求解这个新线性规划,其结果
第一部分绪论 第二部分线性规划与单纯形法 1 判断下列说法是否正确: (a)图解法同单纯形法虽然求解的形式不同,但从几何上理解,两者是一致的; (b)线性规划模型中增加一个约束条件,可行域的范围一般将缩小,减少一个约束条件,可行域的范围一般将扩大; (c)线性规划问题的每一个基解对应可行域的一个顶点; (d)如线性规划问题存在可行域,则可行域一定包含坐标的原点; (e)对取值无约束的变量x i,通常令其中 ,在用单纯形法求得的最优解中有可能同时出现 (f)用单纯形法求解标准型的线性规划问题时,与对应的变量都可以被选作换入变量; (g)单纯形法计算中,如不按最小比值原则选取换出变量,则在下一个解中至少有一个基变量的值为负; (h)单纯形法计算中,选取最大正检验数δk对应的变量x k作为换入变量,将使目标函数值得到最快的增长; (i)一旦一个人工变量在迭代中变为非基变量后,则该变量及相应列的数字可以从单纯形表中删除,而不影响计算结果; (j)线性规划问题的任一可行解都可以用全部基可行解的线性组合表示; (k)若x1,x2分别是某一线性规划问题的最优解,则 也是该线性规 划问题的最优解,其中λ1,λ2可以为任意正的实数; (1)线性规划用两阶段法求解时,第一阶段的目标函数通常写为 X ai为人工变量),但也可写为,只要所有 k i均为大于零的常数; (m)对一个有n个变量、m个约束的标准型的线性规划问题,其可行域的顶点恰好 为个; (n)单纯形法的迭代计算过程是从一个可行解转转换到目标函数值更大的另一个可行解; (o)线性规划问题的可行解如为最优解,则该可行解一定是基可行解; (p)若线性规划问题具有可行解,且其可行域有界,则该线性规划问题最多具有有限个数的最优解; (q)线性规划可行域的某一顶点若其目标函数值优于相邻的所有顶点的目标函数值,则该顶点处的目标函数值达到最优;
运筹学 结课大作业 姓名:苏同锁 学号:1068132104 学院:数理与生物工程学院 班级:数学2010
实例:有三家物流企业将一批货物分别运送到四个城市。物流公司A,B,C所运送货物量分别为110吨、70吨、100吨四个城市I, Il,III,Ⅳ,需求量分别为60吨、70吨、50吨、70吨。物流公司A往城市I,II,III,Ⅳ每吨的运价分别为l0元、15元、20元、25元;物流公司 B到城市I,II,III,Ⅳ每吨的运价分别为2O元、10元、l5元、15元:物流公司 C 到城市I,II,III,Ⅳ每吨的运价分别为25元、30元、20元、25元。 运输费用数据表 如何确定调运方案,才能使运输总费用最小。 首先,设运输总费用为f,我们要求运输总费用最小,故目标函数为:Minf=10x11+15x12+20x13+25x14+20x21+10x22+15x23+15x24+25x31+ 30x32+20x33+25x34 其中Xij表示从物流公司i调运到城市j物资的数量,minf表示运输费用最少。 考虑约束条件如上表所述的量和销地的需求量要满足运输平衡条件,以及各变量取非负数,于是可得如下约束条件:
x11+x12+x13+x14<=110 x21+x22+x23+x24<=70 x31+x32+x33+x34<=100 x11+x21+x31>=60 x12+x22+x32>=70 x13+x23+x33>=50 x14+x24+x34>=70 Xij≥0(i=1,2,3;j=1,2,3,4) 最后,我们将目标函数和约束条件写在一起,就得到了物资调运问题的数学模型,即线性规划问题: minf=10x11+15x12+20x13+25x14+20x21+10x22+15x23+15x24+25x31+ 30x32+20x33+25x34 x11+x12+x13+x14<=110 x21+x22+x23+x24<=70 x31+x32+x33+x34<=100 x11+x21+x31>=60 x12+x22+x32>=70 x13+x23+x33>=50 x14+x24+x34>=70 Xij≥0(i=1,2,3;j=1,2,3,4)