
初中几何模型与解法:等面积法
教学目标
1、学会寻找同一个图形两种计算面积的方法,列出等量关系;
2、学会运用等面积法建立等式求解线段长或证明线段之间的数量关系
3、学会运用等面积法巧妙求解一些不规则图形的面积
重、难点重点:运用等面积法建立等式;难点:运用等面积法巧妙求解一些不规则图形的面积
知识导图
知识梳理
方法概述:运用同一图形的两种计算面积的方法,列出等量关系,从而求解线段的长度,或者证明线段之间的等量关系,甚至求解不规则图形的面接!
技巧归纳:
1、当图形中出现两个(或者以上)的垂直关系时,常用此法.
2、计算多边形面积的常用方法:
(1)面积计算公式
(2)对于公式⑤的证明(如右图):
S= S△ABD+S△CBD
=
=
=
* (3)割补法:将不规则图形“分割或补全’为规则图形.
+
=
又∵ABC= AC AB
∴该直角三角形斜边AB上的高
CD=
导学一:等面积法在直角三角形的应用
知识点讲解1
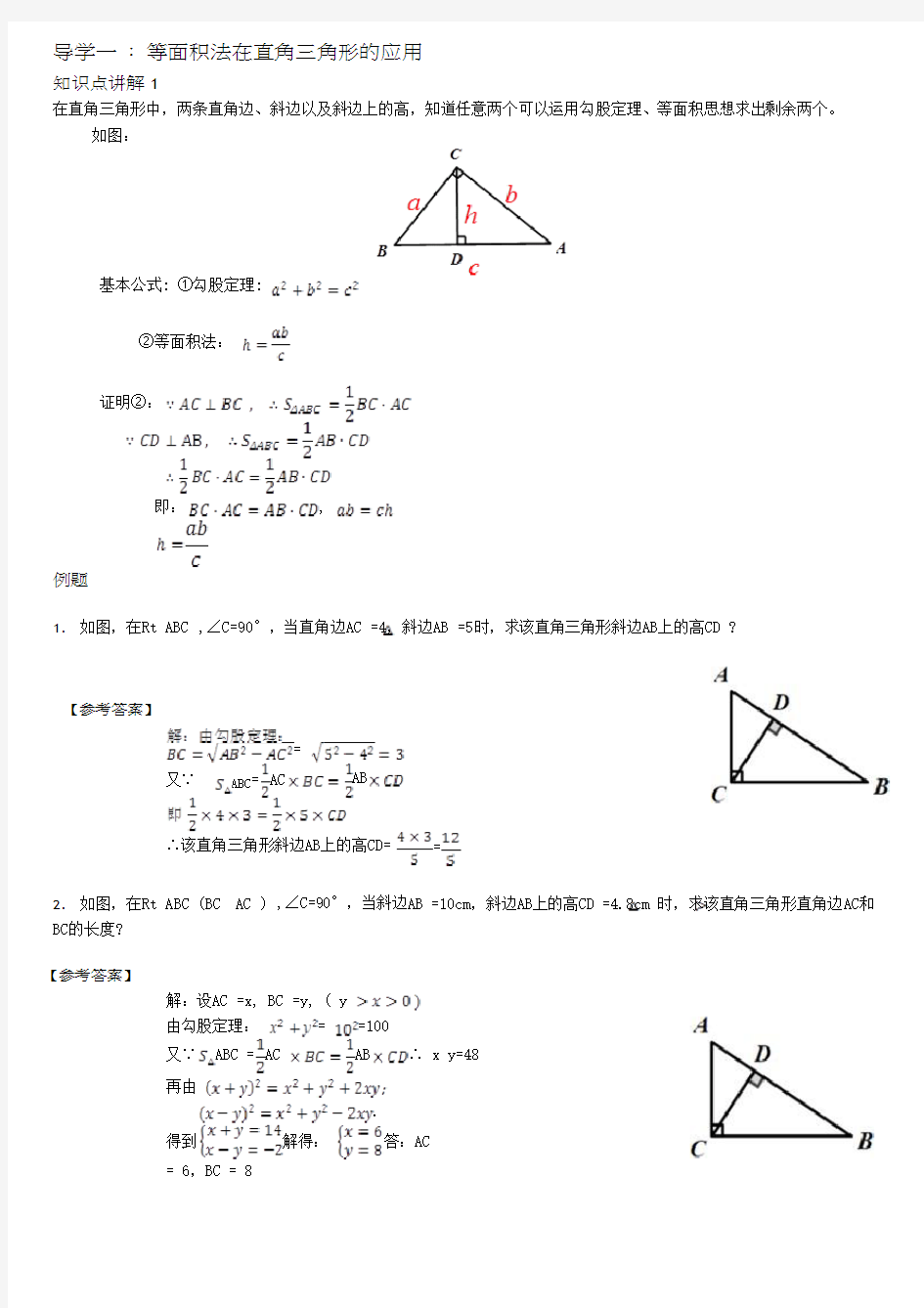
在直角三角形中,两条直角边、斜边以及斜边上的高,知道任意两个可以运用勾股定理、等面积思想求出剩余两个。
如图:
基本公式: ①勾股定理:
②等面积法:
证明②:
即:,
例题
1.如图,在Rt ABC ,∠C=90°,当直角边AC =4,斜边AB =5时,求该直角三角形斜边AB上的高CD ?
【参考答案】
=
2.如图,在Rt ABC (BC AC ) ,∠C=90°,当斜边AB =10cm,斜边AB上的高CD =4.8cm 时,求该直角三角形直角边AC和BC的长度?
【参考答案】
解:设AC =x, BC =y, ( y
由勾股定理:= =100
又∵ABC = AC AB ∴ x y=48
再由
.
得到解得:答:AC
= 6,BC = 8
同步练习
1.如图,在Rt ABC,∠C=90°,且AC=24, BC=7,作 ABC 的三个内角的角平分线交于点P,再过点P 依次作PD⊥AB于D,作PE⊥BC于E, 作PF⊥AC于F .
(1)求证: PD = PE = PF ;
(2)求出: PD的值.
【参考答案】
(1)证明
∵AP 平分∠CAB,且PD ⊥ AB,PF ⊥ AC
∴PD=PF 同理,PD =PE
综上,PD=PE=PF
(2)解:
C 、
=
5
设: PD=PE=PF=d ABC = AC
= 84
sp; ABC&en=
APB
BPC
CPA
84 = + +
d =3, PD=3
2. 如图,△ABC的顶点A ,B ,C 在边长为1的正方形网格的格点上,则BC 边长的高为( )
B 、
D 、
A 、
【参考答案】C
解:∵S △ABC =3×4? ×2×3? ×2×1? ×2×4=4 ∵BC=
= ,
∴BC边长的高= =
故选:C .
导学二 : 等面积法在等腰三角形的应用
知识点讲解 1
在等腰三角形中,可以运用“割补法”的等面积思想,先建立有关“腰以及腰上的高”的等式,再通过等式两边约分来 探索出线段之间的数量关系!
例题
1.如图,在△ABC中, AB=AC, AC 边上的高BD=10cm.
(1)如图1,求AB 边上高CE 的长;
(2)如图2,若点P 为BC 边上任意一点, PM⊥AB 于点M, PN⊥AC 于点N,求PM+PN 的值;
(3)如图3,若点P 为BC 延长线上任意一点,PM⊥AB 于M,PN⊥AC 于点N,在①PM+PN ;②PM PN 中有一个是定值,判断出来并求值.
【参考答案】
(1)由S△ABC= ×AB×CE = ×AC×BD
∵AB=AC, BD=10 ∴CE=10
(2)如图,连接AP
由S△ABP+S△ACP=S△ABC
×AB ×PM + ×AC ×PD = ×AC×BD
∵AB=AC, BD=10
∴PM +PN =10
(3) 如图,连接AP
PM?PN 是定值
理由如下:
连接AP,由S△ABP?S△ACP= S△ABC
×AB ×PM ?× AC ×PD = ×AC×BD
∵AB =AC ,BD =10
∴PM?PN =10
2.已知等边△ABC和内部一点P,设点P 到△ABC三边的AB、 BC 、 AC 的距离分别是h1,h2,h3,
△ABC 的高为h,问h1、h2、h3 与h 之间有怎样的数量关系?请说明理由。
【参考答案】
如图:
解:
h = h1 + h2 + h3 ,
理由如下:
连接AP、BP、CP,
则 S△ABC=S△ABP+S△BPC+S△ACP
∴ BC AM=AB PD+ C PF+ C PE
即 BC h = AB h1 + C h2 + C h3
又∵△ABC是等边三角形,
∴BC=AB=AC
∴ h = h1 + h2 +h3
同步练习
1.已知等边△ABC和点P,设点P 到△ABC三边的AB、AC、BC 的距离分别是PD h1,PE h2,PF h3,△ABC的高AM为h,若点P 在△ABC外,此时h1、h2、h3 与h 之间有怎样的数量关系?请说明理由.
【提示】
连接AP、BP、CP,
则 S△ABC=S△ABP+S△ACP S△BPC
2.如图,点E在正方形ABCD的对角线AC上,且AE=AD,点P是BE上任一点,PN⊥AB 于点N,PM⊥AC于点M,若正方形ABCD 的面积是12,证明PM+PN是一个定值,并且计算出这个定值.
【参考答案】
如图③,连接AP,过E作EF⊥AB于F,
∵正方形ABCD的面积是12,
∴AB=AE=AD=2 ,
∵四边形ABCD是正方形,
∴∠BAC=45°,
∴△AEF是等腰直角三角形,
∴EF== ,
∵S△AEB=S△AEP+S△ABP,
AB?EF=AB?PN+AE?PM,
∵AE=AB,
∴PM+PN=EF=
导学三:等面积法在勾股定理中的应用
知识点讲解1
勾股定理的证明充分体现了“数形结合思想”,它有500多种证明方法,但几乎每一种都要用到等面积思想. 从几何角度认识代数关系,用等面积思想建立等式进行推导!
勾股定理描述的是三边的平方关系= 因此只要以这个直角三角形三边往外所作图形的面积根对应边的平方成正比(S 小=k , S中=k, S大=k,k是常数)就会有较小的两个图形的面积之和等于较大者的面积.
(即: k k = k,简记为:S 小S中S大)
例题
1.请您运用右下图和如下四个辅助定理:
(1)如果两个三角形有两组对应边和这两组对应边所夹的角相等,则两三角形全等(SAS );
(2)三角形面积是任一等底等高的平行四边形面积的一半;
(3)任意一个正方形的面积等于其边长的平方;
(4)任意一个矩形的面积等于其相邻两边长的乘积;
证明勾股定理:=
【参考答案】
如手拉手模型图:
因为:
△FBC ≌ △ABD (SAS)
△BCI ≌ △ECA (SAS)
所以可设:
FBC = ABD = x
BCI = ECA = y
如上图:
因为:
FBC = ABD = x
ABFG = 2 FBC = 2x
BDLK = ABD = 2x
所以:
ABFG = 2x = BDLK
如上图: 因为: BCI = ECA = y
ACIH BCI = 2y KLEC ECA = 2y
所以:
于是: ABFG = BDLK ACIH KLEC BDLK KLEC =
BDEC
进一步: ABFG ACIH =
BDEC
更进一步:
=
2. 如图①,在△ABC中,∠C=90°,分别以△ABC三边为边向外作三个正方形,其面积分别用S 1,S 2,S 3表示,则不难证
明S 1=S 2+S 3
(1) 如图②,在△ABC中,∠C=90°,分别以△ABC三边为直径向外作三个半圆,其面积分别用S 1,S 2,S 3表示,那么S 1,
S 2,S 3之间有什么关系:(不必证明,直接写出)
(2) 如图③,△ABC中,∠C=90°,分别以△ABC三边为边向外作三个正三角形,其面积分别用S 1,S 2,S 3表示,请你确
定S 1,S 2,S 3之间的关系并加以证明
(3)利用图①的结论,解决下列问题:如图④,Rt△ABC中,∠C=90°,AC =5,BC =8.分别以AB 、AC 、BC 为边在AB 的 同侧作正方形ABEF 、ACPQ 、BCMN ,四块阴影部分的面积分别为S 1,S 2,S 3,S 4.则 S 1+S 2+S 3+S 4=
.
ACIH = 2y
KLEC
【参考答案】
解:(1)如图②,分别以Rt△ABC三边为直径向外作三个半圆,其面积分别用S1、S2、S3表示,那么S1= S2
+S3,
理由为:在Rt△ABC中,利用勾股定理得:AB2=AC2+BC2,
∴AB2=AC2+BC2,即S1=S2+S3;
(2)如图(3),分别以Rt△ABC三边为边向外作三个正三角形,其面积分别用 S1、S2、S3表示,S1、
S2、S3之间的关系为S1=S2+S3,
理由为:在Rt△ABC中,利用勾股定理得:AB2=AC2+BC2,
∴AB2=AC2+BC2,即S1=S2+S3;
(3)如图:
过F作AM的垂线交AM于D,
可证明Rt△ADF≌Rt△ABC,Rt△DFK≌Rt△CAT,
所以S2=S Rt△ABC.
由Rt△DFK≌Rt△CAT可进一步证得:Rt△FPT≌Rt△EMK,
∴S3=S△FPT,
又可证得Rt△AQF≌Rt△ACB,
∴S1+S3=S Rt△AQF=
S Rt△ABC.易证
Rt△ABC≌Rt△EBN,
∴S4=S Rt△ABC,
∴S1+S2+S3+S4
=(S1+S3)+S2+S4
=S Rt△ABC+S Rt△ABC+S Rt△ABC
=S Rt△ABC×3
=5×8÷2×3
=60.
故答案为:60.
同步练习
1.如图,由两个直角三角形和三个大正方形组成的图形,其中阴影部分面积是()
A、16
B、25
C、144
D、169 【参考答案】B
【题目解析】
如图所示:
根据勾股定理得出: AB
===5,
∴EF=AB=5,
∵=
∴阴影部分面积是25,
故选:B.
2.如图,以Rt△ABC的三条边作三个正三角形,则图中S1、S2、S3、S4 的关系为()
A、S1+S2+S3=S4
B、S1+S2=S3+S4
C、S1+S3=S2+S4
D、不能确定
【参考答案】C
【题目解析】如图所示:
设Rt△ABC的三条边AB=c,AC=b,BC=a,
∵△ACG,△BCH,△ABF是等边三角形,
∴S1=S△ACG?S5=b2?S5,
S3=S△BCH?S6=a2?S5,
∴S1 S3= 2 b2) S5?S6
∵S2+S4=S△ABF?S5?S6=c2 S5?S6
且
∴S1 S3=S2+S4
故选C.
3.如图,在Rt△ABC中,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”,当AC=4,BC=2时,则阴影部分的面积为()
A、4
B、4π
C、8π
D、8
【参考答案】A
【题目解析】
如图所示:
设以AB、AC、BC为直径的半圆面积分别为:
、、
其中O、Q、P分别是它们的圆心.
则阴影部分面积= + +
又∵,且=
∴+
∴阴影部分面积= = AC BC=4
故选A.
4.有一个面积为1的正方形,经过第一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过第二次“生长”后,变成了下图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2019次后形成的图形中所有的正方形的面积和是()
A、1
B、2018
C、2019
D、2020
【参考答案】D
【题目解析】勾股树的本质是三个正方形之间的等面积关系
导学四:等面积法在其它图线中的应用
知识点讲解1
题目中出现“高、垂线段、角平分线、中线、平行线”,以及与线段有关的乘积、分式等量,也可以试一试等面积思想
建立等式进行突破!
如上图,若GF=ED,且△PFG的面积△PED的面积,则可以证明射线BP平分, 读者自行证明.
例题
1.如图,△ABC中,AB=4,BC=6,BD 是△ABC的角平分线,DE⊥AB 于点E,AF⊥BC于点F,若DE=2,则AF
的长为()
A、3
B、
C、D、
【参考答案】B
【题目解析】如图:
作DH⊥BC 于H
∵BD 是△ABC 的角平分线,DE⊥AB,DH⊥BC,
∴DH =DE=2,
△ABD 的面积+△CBD 的面积=△ABC 的面积,
∴×4×2+×6×2=×6×AF,
解得,AF=,故选:B
2.平行线分线段成比例亦称“平行截割定理”.平面几何术语是指“三条平行线截两条直线,所得的四条线段对应成比例”.如图,已知∥∥,请连接辅助线AE、BD、CE、BF 作高EH⊥AC于 H, BG ⊥ DF
于G后,请您从面积的角度去证明.
【参考答案】
知
综上得:
证明:如图,
∥
S △ABE = S △DEB ① S △BCE = S △EFB ②
①和②左右相比
同理
【题目解析】平行线之间的等面积抓住同底等高,把面积作商,约分后就得到线段之间的比例
同步练习
1. 如图,把△ABC的BA 边延长1倍到点D, AC 边延长2倍到点F ,点CB 边延长3倍到点E, 连接DE 、EF 、FD,得到△DEF.已知
△DEF的面积为54,△ABC的面积是 .
A 、 1
B 、 3
C 、 6
D 、 9
【参考答案】
如图,连接CD 、AE 、
BF
知:
即:
设 ,则
,
,
进一步∵
,
,
=
∴
即
【题目解析】
等面积思想建立等式 由
,推出
2. 如图BE 、CF 分别是 ABC 的中线,且BE=CF , AM⊥CF 于M ,AN⊥BE 于N ,求证:AM=AN 。
【参考答案】
【题目解析】
∵BE、CF 分别是 ABC 的中线
且BE=CF,∴AM=AN
等面积思想建立等式 由
,推出
∴ 即
∴ , 同理
B 、
C 、
C 、
课后练习
1. 如左图,在直角三角形中,任意一个锐角“∠A的对边与斜边的比”叫做
∠A的正弦,记作SinA (由英语sine 简写),即SinA= .再看右图,在2 2正方形网格中,△ABC的顶点均在
格 点 上 , 则 Sin CAB=( ).
A 、
D 、
【参考答案】B 【题目解析】
如图:
过C 作CD⊥AB,
根据勾股定理得: AB =
= ,
S△ABC=4?1? ?1= = CD?AB= CD? , 解得:CD =
则Sin CAB
2. 已知:如图,矩形ABCD 中,AB =5,BC =12,对角线AC 、BD 相交于点O ,点P 是线段AD 上任意一点,且PE⊥BD于点E ,
PF⊥AC于点F ,则PE +PF 等于( ).
A 、
B 、 D 、
【参考答案】C 【题目解析】
解:如图,连接PO ,
∵矩形ABCD的两边AB=5,BC=12,
∴S矩形ABCD=AB?BC=60,OA=OC,OB=OD,AC=BD,
AC===13,
∴S△AOD= S矩形ABCD=15,OA=OD= AC=,
∴S△AOD=S△AOP+S△DOP=OA?PE+OD?PF= OA(PE+PF)=××(PE+PF)=15,
∴PE+PF=,
故选:C.
3.如图已知四边形ABCD是菱形,对角线AC、BD相交于点O,且AC
=6,BD=8.AE⊥BC于E,则AE=()
D、4
A、5
B、C、
【参考答案】B
【题目解析】
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=3,OB=OD=4,
∴BC==5,
∵ ?AC?BD=BC?AE,
∴AE=,
故选:B.
4.正方形ABCD的边长为1,其面积记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积为S2,…按此规律继续下去,则S5的值为()
A、
C、D、
【参考答案】A
【题目解析】
在图中标上字母E,如图所示.
∵正方形ABCD的边长为1,△CDE为等腰直角三角形,
∴DE2+CE2=CD2,DE=CE,
∴S2+S2=S1.
观察,发现规律:S1=12=1,S2=S1=,S3=S2=,S4=S3=,…,
∴S n=.
当n=5时,S5==,
故选:A.
5.如图,在矩形ABCD中,AB=3,BC=2,O是AD的中点,连接OB、OC,点E在线段BC上(点E不与点B、C重合),过点E 作EM⊥OB于M,EN⊥OC于N,则EM+EN的值为()
A、6
B、1.5
【参考答案】D
【题目解析】C、D、
B、
中考直通车·数学广州分册 第八章专题拓展 第24讲常见几何模型
【考点解读】 常见几何模型是广州市中考的压轴题常考题型,主要以考察选择、填空最后一题和几何压轴题为主。几何模型类型较多,综合性强,属于中考中重点但同样是难点的一个考点。 【考点分析】 2011年 考查三角形全等和三角形中位线性质,标准的手拉手模型。 2014年 考查三角形全等的判断和性质,根据手拉手模型找出全等三角形,再应用其性质 2016年 本年度模型思想明显,分值占比大,主要考查三角形全等的判定及其性质、图像的旋转,利用模型思想作为解题突破口顺利完成辅助线。 【模型介绍】 手拉手模型: 1、 【条件】 如图两个等边三角形ABD ?与BCE ?,连结 AE 与CD , 【结论】(1)DBC ABE ??? (2)DC AE = (3)AE 与DC 之间的夹角为? 60 (4)AE 与DC 的交点设为H , BH 平分AHC ∠
C D A B F E C D 2、 【条件】如图两个等腰直角三角形ADC 与EDG ,连结CE AG ,,二者相交于点H 。 【结论】 (1)CDE ADG ???是否成立? (2)AG =CE (3)AG 与CE 之间的夹角为 90 (4)HD 是否平分AHE ∠? 旋转模型: 一、邻角相等对角互补模型 【条件】如图,四边形ABCD 中,AB =AD ,90BAD BCD ?∠=∠= 【结论】45ACB ACD BC CD ? ∠=∠=+= ① ② 二、角含半角模型:全等 角含半角要旋转:构造两次全等 F E D C B A G F E D C B A A C D E A C D E F
中考数学几何模型2:共顶点模型 共顶点模型,亦称“手拉手模型”,是指两个顶角相等的等腰或者等边三角形的顶点重合,两个三角形的两条腰分别构成的两个三角形全等或者相似。寻找共顶点旋转模型的步骤如下: (1)寻找公共的顶点 (2)列出两组相等的边或者对应成比例的边 (3)将两组相等的边分别分散到两个三角形中去,证明全等或相似即可。 两等边三角形 两等腰直角三角形 两任意等腰三角形 *常见结论: 连接BD 、AE 交于点F ,连接CF ,则有以下结论: (1)BCD ACE ?△△ (2)AE BD = (3)AFB DFE ∠=∠ (4)FC BFE ∠平分 例题1. 以点A 为顶点作等腰Rt △ABC ,等腰Rt △ADE ,其中∠BAC =∠DAE =90°,如图1所示放置,使 得一直角边重合,连接BD 、CE . (1)试判断BD 、CE 的数量关系,并说明理由; (2)延长BD 交CE 于点F 试求∠BFC 的度数; (3)把两个等腰直角三角形按如图2放置,(1)、(2)中的结论是否仍成立?请说明理由.
变式练习>>> 1. 已知:如图,△ABC和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°. (1)求证:BD=AE. (2)若∠ABD=∠DAE,AB=8,AD=6,求四边形ABED的面积. 例题2. 如图,等边△ABC,等边△ADE,等边△DBF分别有公共顶点A,D,且△ADE,△DBF都在△ADB内,求证:CD与EF互相平分.
变式练习>>> 2. 已如图,已知等边三角形ABC,在AB上取点D,在AC上取点E,使得AD=AE,作等边三角形PCD,QAE和RAB,求证:P、Q、R是等边三角形的三个顶点. 例题3. 在等边△ABC与等边△DCE中,B,C,E三点共线,连接BD,AE交于点F,连接CF. (1)如图1,求证:BF=AF+FC,EF=DF+FC;
初中数学几何公式 1过两点有且只有一条直线 2两点之间线段绘短 3同角或等角的补角相等 4同角或等角的余角相等 5过一点有且只有一条直线和己知直线垂直 6直线外一点与直线上各点连接的所有线段中,垂线段最短 7平行公理经过直线外一点,有且只有一条直线与这条直线平行 8如果两条直线都和第三条直线平行,这两条直线也互相平行 9同位角相等,两直线平行 10内错角相等,两直线平行 11同旁内角互补,两直线平行 12两II线平行,同位角相等 n两直线平行,内错角相等 14两直线平行,同旁内角互补 15定理三角形两边的和人于第三边 16推论三角形两边的差小于第三边 17三角形内角和定理三角形三个内角的和等于180? 18推论2直角三角形的两个锐角互余 19推论2三角形的-个外角等于和它不相邻的两个内角的和 20推论3三角形的一个外角大于任何一个和它不相邻的内角 21全等三角形的对应边、对应角相等 22边角边公理(SAS)令两边和它们的夹角对应相等的两个三角形全等 23角边角公理(ASAMj两角和它们的夹边对应相等的两个三角形全等 24推论(AAS)有两角和其中一角的对边对应相等的两个三角形全等 25边边边公理(SSS)有三边对应相等的两个三角形全等 26斜边、直角边公理(HL)右斜边和一条直角边对应用等的两个直角三角形全等 27定理1在角的平分线上的点到这个角的两边的距离相等 28定理2到一个角的两边的距离相同的点,在这个角的平分线上 29角的平分线是到角的两边距离相等的所有点的集合 30等腰三角形的性质定理等腰三角形的两个底角相等(即等边对等角) 31推论1等腰三角形顶角的平分线平分底边并且垂直于底边 32等腰三角形的顶角平分线、底边匕的中线和底边上的高互相旋合 33推论3等边三角形的各角都柑等,并且每一个角都等于60。 34等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边) 35推论1三个角都相等的三角形是等边三角形 36推论2有一个角等于60。的等腰三角形是等边三角形 37在直角三角形中,如果一个锐角等于30。那么它所对的直角边等于斜边的一半 38直角三角形斜边上的中线等于斜边上的一半
中考必考几何模型(猿辅导) 最 新 讲 义
相似模型 模型1:A、8模型 已知∠1=∠2 结论:△ADE∽△ABC 模型分析 如图,在相似三角形的判定中,我们通过做平行线,从而得出A型或8型相似.在做题使,我们也常常关注题目由平行线所产生的相似三角形. 模型实例 【例1】如图,在ABC中,中线AF、BD、CE相交于点O,求证: 1 2 OF OE OD OA OC OB ===. 解答:证法一:如图①,连接DE.∵D、E是中点,∴ 1 2 DE BC =.,DE//BC ∴△EOD∽△COB(8模型)∴ 1 2 OE DE OC BC ==.同理: 1 2 OF OA =, 1 2 OD OB =. ∴ 1 2 OF OE OD OA OC OB ===.
证法二:如图②,过F作FG//AC交BD于点G,∵F是中点,∴ 1 2 GF BF AD BC ==. ∵AD=CD, ∴ 1 2 GF AD =.∵FG//AD,∴△GOF∽△DOA(8模型) ∴ 1 2 OF GF OA AD ==.同理 1 2 OE OC =, 1 2 OD OB =.∴ 1 2 OF OE OD OA OC OB ===. 【例2】如图,点E、F分别在菱形ABCD的边AB、AD上,且AE=DF,BF交DE于点G, 延长BF交CD的延长线于H,若AF DF =2,求 HF BG 的值. 解答:∵四边形ABCD是菱形,∴AB=BC=CD=AD. 设DF=a,则DF=AE=a,AF=EB=2a.∵HD//AB,∴△HFD∽△BF A ∴ 1 2 HD DF HF AB AF FB ===,∴HD=1.5a, 1 3 FH BH =,∴FH= 1 3 BH ∵HD//EB,∴△DGH∽△EGB,∴ 1.53 24 HG HD a GB EB a ===,∴ 4 7 BG HB = ∴BG=4 7 HB,∴ 1 7 3 412 7 BH HF BG BH == 跟踪练习: 1.如图,D、E分别是△ABC的边AB、BC上的点,且DE//AC,AE、CD相交于点O,若S△DOE:S△COA=1:25.则S△BD E与S△CDE的比是____________.
苏科版初中数学几何定理定义公式大全 班级学号姓名以下标注真命题的条目,解答题时要先证明,再使用。未标注的定理、定义、公式可以直接使用。 第一部分相交线、平行线 1、直线公理:经过两点有且只有一条直线(两点确定一直线)。 2 、线段公理:两点之间线段最短。 3、同角或等角的补角相等,同角或等角的余角相等。 4、对顶角相等。 5、垂线的性质: ①经过一点 ..有且只有一条直线和已知直线垂直。 ②直线外一点与直线上各点连接的所有线段中,垂线段最短。(简写为:垂线段最短。) 6、平行线的定义:在同一平面内不相交的两条直线叫作平行线。 7、在同一平面中两条直线的位置关系有两种,相交和平行。 在空间几何中两条直线的位置关系有三种,相交、平行和异面。 8、平行公理:经过直线外一点 .....,有且只有一条直线与这条直线平行。 7、平行公理的推论:如果两条直线都和第三条直线平行,这两条直线也互相平行。 9、平行线的判定: ①同位角相等,两直线平行。 ②内错角相等,两直线平行。 ③同旁内角互补,两直线平行。 10、平行线的性质: ①两直线平行,同位角相等。 ②两直线平行,内错角相等。 ③两直线平行,同旁内角互补。 10、三视图(略) 第二部分三角形 1、三角形的定义:由不在同一直线上的三条线段首尾顺次相接组成的图形,叫作三角形。 2、三角形的中线:连接三角形的一个顶点和对边中点的线段叫作三角形的中线。 3、三角形的角平分线:三角形的一个内角的平分线与对边相交,顶点和交点之间的线段叫作三角形的角平分线。
4、三角形的高:经过三角形的一个顶点向对边所在直线作垂线,顶点和垂足之间的线段叫作三角形的高。 5、三角形三边关系定理:三角形两边的和大于第三边,三角形两边的差小于第三边。 6、三角形内角和定理:三角形三个内角的和等于180° 7、推论:三角形的一个外角等于和它不相邻的两个内角的和。 8、真命题:三角形的一个外角大于任何一个和它不相邻的内角。 9、多边形的内角和公式:N=(n-2)180° 10、任意多边的外角和等于360°。 11、连接多边形的不相邻顶点的直线叫作对角线。从n 边形(n ≥3)的一个顶点可以引(n-3)条对角线,n 边形(n ≥3)一共有)3(2 1 n n 条对角线。 12、能够完全重合的两个图形叫作全等形。 13、能够完全重合的两个三角形叫作全等三角形。全等三角形的对应边、对应角相等 。 14、全等三角形的判定: ①边角边(SAS):有两边和它们的夹角对应相等的两个三角形全等。 ②角边角( ASA):有两角和它们的夹边对应相等的两个三角形全等 。 ③角角边(AAS) :有两角和其中一角的对边对应相等的两个三角形全等。 ④边边边(SSS) :有三边对应相等的两个三角形全等。 ⑤斜边、直角边(HL) :有斜边和一条直角边对应相等的两个直角三角形全等 第三部分 轴对称图形 1、轴对称:如果把一个图形沿着一条直线折叠后能够与另一个图形完全重合,那么这两个图形关于直线成轴对称。 2、轴对称图形:如果把一个图形沿着一条直线折叠后,直线两旁的部分能够完全重合,那么这个图形是轴对称图形。 3、轴对称的性质: ①关于某条直线对称的两个图形是全等形。 ②如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线。 ③两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上。 ④真命题:如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称。
初中数学常用公式 一?代数: 1.1绝对值运算 2.1平面几何:角 1.2有理数的运算 2.2 三角形 1.3整式的乘法运算 2.3四边形 1.4整式乘法公式 2.4比例性质 1.5整式除法公式 2.5三角函数 1.6分式的运算公式 2.6与圆有关的公式1.7 一兀二次方程 2.7点与圆的位置1.8因式分解 2.8直线与圆的位置1.9不等式 2.9两圆的位置 1.10二次根式 1.1绝对值运算 1.2有理数的运算 1.3整式的乘法运算
1.4 整式乘法公式 1.5 整式除法公式 1.6 分式的运算公式 1.7 一元二次方程:的解1.8 因式分解
1.9 不等式若,则 若,则 若,则 1.10 二次根式 2.1 角 1周角=360 ° 1 平角=180 ° 1 直角=90 ° 1°= 60 ;1 = 60”若,则/ A与/ B互为余角。 若,则/ A与/ B互为补角。 2.2 三角形 若,则 若,则 若,则为直角三角形
正弦定理: 余弦定理: 2.3 四边形 (a为底边长,h为底边上的高)(ab 为两邻边长) (ab 为菱形的两条对角线) 2.4 比例性质 若,则 若,则 2.5 三角函数
2.6 与圆有关的公式 圆周长 圆面积 弧长 扇形面积 2.7 点与圆的位置 设P点到圆心的距离为d,圆的半径长为r,则点P 在圆上 点P 在圆内 点P 在圆外 2.8 直线与圆的位置 设圆心到直线的距离为d,圆半径长为r,则
直线与圆相切 直线与圆相离 直线与圆相交 2.9 两圆的位置 设两圆半径分别为R和r,圆心距为d,则 两圆外离 两圆外切 两圆相交 两圆内切 两圆内含
半角模型 已知如图:①∠2=1 2 ∠AOB;②OA=OB. O A B E F 1 23 连接FB,将△FOB绕点O旋转至△FOA的位置,连接F′E,FE,可得△OEF≌△OEF′ 43 2 1 F' F E B A O 模型分析 ∵△OBF≌△OAF′, ∴∠3=∠4,OF=OF′. ∴∠2=1 2 ∠AOB, ∴∠1+∠3=∠2 ∴∠1+∠4=∠2 又∵OE是公共边, ∴△OEF≌△OEF′. (1)半角模型的命名:存在两个角度是一半关系,并且这两个角共顶点; (2)通过先旋转全等再轴对称全等,一般结论是证明线段和差关系; (3)常见的半角模型是90°含45°,120°含60°. 模型实例 例1 已知,正方形ABCD中,∠MAN=45°,它的两边分别交线段CB、DC于点M、N.(1)求证:BM+DN=MN. (2)作AH⊥MN于点H,求证:AH=AB.
证明:(1)延长ND 到E ,使DE=BM , ∵四边形ABCD 是正方形,∴AD=AB . 在△ADE 和△ABM 中, ?? ? ??=∠=∠=BM DE B ADE AB AD ∴△ADE ≌△ABM . ∴AE=AM ,∠DAE=∠BAM ∵∠MAN=45°,∴∠BAM+∠NAD=45°. ∴ ∠MAN=∠EAN=45°. 在△AMN 和△AEN 中, ?? ? ??=∠=∠=AN AN EAN M AN EA M A ∴△AMN ≌△AEN . ∴MN=EN . ∴BM+DN=DE+DN=EN=MN . (2)由(1)知,△AMN ≌△AEN . ∴S △AMN =S △AEN . 即EN AD 2 1 MN AH 21?=?. 又∵MN=EN , ∴AH=AD . 即AH=AB .
初中数学几何公式 1 过两点有且只有一条直线 2 两点之间线段最短 3 同角或等角的补角相等 4 同角或等角的余角相等 5 过一点有且只有一条直线和已知直线垂直 6 直线外一点与直线上各点连接的所有线段中,垂线段最短 7 平行公理经过直线外一点,有且只有一条直线与这条直线平行 8 如果两条直线都和第三条直线平行,这两条直线也互相平行 9 同位角相等,两直线平行 10 错角相等,两直线平行 11 同旁角互补,两直线平行 12 两直线平行,同位角相等 13 两直线平行,错角相等 14 两直线平行,同旁角互补 15 定理三角形两边的和大于第三边 16 推论三角形两边的差小于第三边 17 三角形角和定理三角形三个角的和等于180° 18 推论1 直角三角形的两个锐角互余 19 推论2 三角形的一个外角等于和它不相邻的两个角的和 20 推论3 三角形的一个外角大于任何一个和它不相邻的角 21 全等三角形的对应边、对应角相等 22 边角边公理(SAS) 有两边和它们的夹角对应相等的两个三角形全等 23 角边角公理( ASA)有两角和它们的夹边对应相等的两个三角形全等 24 推论(AAS) 有两角和其中一角的对边对应相等的两个三角形全等 25 边边边公理(SSS) 有三边对应相等的两个三角形全等 26 斜边、直角边公理(HL) 有斜边和一条直角边对应相等的两个直角三角形全等 27 定理1 在角的平分线上的点到这个角的两边的距离相等 28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上 29 角的平分线是到角的两边距离相等的所有点的集合 30 等腰三角形的性质定理等腰三角形的两个底角相等 (即等边对等角) 31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边 32 等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合 33 推论3 等边三角形的各角都相等,并且每一个角都等于60° 34 等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边) 35 推论1 三个角都相等的三角形是等边三角形 36 推论 2 有一个角等于60°的等腰三角形是等边三角形 37 在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半 38 直角三角形斜边上的中线等于斜边上的一半 39 定理线段垂直平分线上的点和这条线段两个端点的距离相等 40 逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上 41 线段的垂直平分线可看作和线段两端点距离相等的所有点的集合
初中几何常见模型解析 模型一:手拉手模型-旋转型全等 (1)等边三角形 ?条件:均为等边三角形 ?结论:①;②;③平分。 (2)等腰 ?条件:均为等腰直角三角形 ?结论:①;②; ?③平分。 (3)任意等腰三角形 ?条件:均为等腰三角形 ?结论:①;②; ?③平分 模型二:手拉手模型-旋转型相似 (1)一般情况 ?条件:,将旋转至右图位置 ?结论: ?右图中①; ?②延长AC交BD于点E,必有 (2)特殊情况 ?条件:,,将旋转至右图位置 ?结论:右图中①;②延长AC交BD于点E,必有; ③; ④; ⑤连接AD、BC,必有; ⑥(对角线互相垂直的四边形)
模型三:对角互补模型 (1)全等型-90° ?条件:①;②OC平分 ?结论:①CD=CE; ②;③ ?证明提示: ①作垂直,如图,证明; ②过点C作,如上图(右),证明; ?当的一边交AO的延长线于点D时: 以上三个结论:①CD=CE(不变); ②;③ 此结论证明方法与前一种情况一致,可自行尝试。 (2)全等型-120° ?条件:①; ?②平分; ?结论:①;②; ?③ ?证明提示:①可参考“全等型-90°”证法一; ②如图:在OB上取一点F,使OF=OC,证明 为等边三角形。 (3)全等型-任意角 ?条件:①;②; ?结论:①平分;②; ?③. ?当的一边交AO的延长线于点D时(如右上图): 原结论变成:①; ②; ③; 可参考上述第②种方法进行证明。请思考初始条件的变化对模型的影响。 ?对角互补模型总结: ①常见初始条件:四边形对角互补;注意两点:四点共圆及直角三角形斜边中线; ②初始条件“角平分线”与“两边相等”的区别; ③两种常见的辅助线作法; ④注意平分时,相等如何推导?
轴对称图形 1、轴对称:如果把一个图形沿着一条直线折叠后能够与另一个图形完全重合,那么这两个图形关于直线成轴对称。 2、轴对称图形:如果把一个图形沿着一条直线折叠后,直线两旁的部分能够完全重合,那么这个图形是轴对称图形。 3、轴对称的性质: ①关于某条直线对称的两个图形是全等形。 ②如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线。 ③两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上。 ④真命题:如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称。 5、线段的轴对称性: ①线段的垂直平分线上的点到线段两端的距离相等。 ②到线段两端距离相等的点在这条线段的垂直平分线上。 ③线段的垂直平分线是到线段两端距离相等的所有点的集合。 6、角的轴对称性: ①角平分线上的点到这个角的两边的距离相等。 ②在角的内部到一个角的两边的距离相同的点,在这个角的平分线上。 ③角的平分线是角的内部到角的两边距离相等的所有点的集合。 7、等腰三角形的定义:有两条边相等的三角形叫作等腰三角形。 8、等腰三角形的性质: ①等腰三角形的两个底角相等 (即等边对等角) ②三线合一:等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合。 9、等腰三角形的判定:如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边) 10、等边三角形的定义:三边都相等的三角形叫作等边三角形。
11、等边三角形的性质:等边三角形的各角都相等,并且每个角都等于60°。 12、等边三角形的判定: ①三个角都相等的三角形是等边三角形。 ②有一个角等于60°的等腰三角形是等边三角形。 13、直角三角形的性质: ①直角三角形的两个锐角互余。 ②直角三角形斜边上的中线等于斜边上的一半 ③勾股定理:直角三角形的两条直角边的平方和等于斜边的平方。 ④在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半。 ⑤在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30 14、直角三角形的判定: ①两个锐角互余的三角形是直角三角形。 ②真命题:如果三角形的一边上的中线等于这边长的一半,那么这个三角形是直角三角形。 ③勾股定理逆定理:如果一个三角形的两条边的平方和等于第三条边的平方,那么这个三角形是直角三角形。
初三数学公式大全 小编为大家整理了有关几何体部分的所有初三数学公式大全进行了汇总,方便大家查阅记忆。 1 过两点有且只有一条直线 2 两点之间线段最短 3 同角或等角的补角相等 4 同角或等角的余角相等 5 过一点有且只有一条直线和已知直线垂直 6 直线外一点与直线上各点连接的所有线段中,垂线段最短 7 平行公理经过直线外一点,有且只有一条直线与这条直线平行 8 如果两条直线都和第三条直线平行,这两条直线也互相平行 9 同位角相等,两直线平行 10 内错角相等,两直线平行 11 同旁内角互补,两直线平行 12两直线平行,同位角相等 13 两直线平行,内错角相等 14 两直线平行,同旁内角互补 15 定理三角形两边的和大于第三边 16 推论三角形两边的差小于第三边
17 三角形内角和定理三角形三个内角的和等于 180° 18 推论1 直角三角形的两个锐角互余 19 推论2 三角形的一个外角等于和它不相邻的两个内角的和 20 推论3 三角形的一个外角大于任何一个和它不相邻的内角 21 全等三角形的对应边、对应角相等 22 边角边公理(SAS) 有两边和它们的夹角对应相等的两个三角形全等 23 角边角公理( ASA)有两角和它们的夹边对应相等的两个三角形全等 24 推论(AAS) 有两角和其中一角的对边对应相等的两个三角形全等 25 边边边公理(SSS) 有三边对应相等的两个三角形全等 26 斜边、直角边公理(HL) 有斜边和一条直角边对应相等的两个直角三角形全等 27 定理1 在角的平分线上的点到这个角的两边的距离相等28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上 29 角的平分线是到角的两边距离相等的所有点的集合 30 等腰三角形的性质定理等腰三角形的两个底角相等
面积公式A bc B ac C ab S ABC sin 2 1sin 21sin 21===? ))()((c p b p a p p S ABC ---=? 2/)(c b a p ++= 和角公式 A B B A B A cos sin cos sin )sin(+=+ A B B A B A sin sin cos cos )cos(-=+ B A B A B A tan tan 1tan tan )tan(-+=+ 差角公式 A B B A B A cos sin cos sin )sin(-=- A B B A B A sin sin cos cos )cos(+=- B A B A B A tan tan 1tan tan )tan(+-=-
常用角度的三角比
相关练习题: 1.已知ABC ?中,,75 =∠B ,60 =∠C ,10=BC 求AB 与AC 的长及三角形的面积 2.求证面积公式A bc B ac C ab S ABC sin 2 1sin 21sin 21===? 3.求证海伦公式 ))()((c p b p a p p S ABC ---=? 2/)(c b a p ++= 4. 已知ABC ?中,,7=AB ,8=BC ,9=AC 求sinA , sinB , sinC 5.在等腰三角形ABC 中,AB=1,∠A=900,点E 为腰AC 中点,点F 在底边BC 上,且FE ⊥BE ,求△CEF 的面积。 6.已知四边形ABCD 内接于直径为3的圆O ,对角线AC 是直径,对角线AC 和BD 的交点是P ,AB=BD ,且PC=0.6,求四边形ABCD 的周长. 7.在△ABC 中,∠ABC =600,点P 是△ABC 内的一点,使得∠APB =∠BPC =∠CPA ,且PA =8,PC =6,则PB = 。 A B C E F A B C P
初中数学几何知识点总结大全 今天小编为大家整理了一篇有关初中数学几何知识点的相关内容,希望对大家有所帮助。 1、过两点有且只有一条直线 2、两点之间线段最短 3、同角或等角的补角相等 4、同角或等角的余角相等 5、过一点有且只有一条直线和已知直线垂直 6、直线外一点与直线上各点连接的所有线段中,垂线段最短 7、平行公理经过直线外一点,有且只有一条直线与这条直线平行 8、如果两条直线都和第三条直线平行,这两条直线也互相平行 9、同位角相等,两直线平行 10、内错角相等,两直线平行 11、同旁内角互补,两直线平行 12、两直线平行,同位角相等 13、两直线平行,内错角相等 14、两直线平行,同旁内角互补 15、定理三角形两边的和大于第三边 16、推论三角形两边的差小于第三边 17、三角形内角和定理三角形三个内角的和等于180° 18、推论1直角三角形的两个锐角互余 19、推论2三角形的一个外角等于和它不相邻的两个内角的和 20、推论3三角形的一个外角大于任何一个和它不相邻的内角
21、全等三角形的对应边、对应角相等 22、边角边公理(SAS)有两边和它们的夹角对应相等的两个三角形全等 23、角边角公理(ASA)有两角和它们的夹边对应相等的两个三角形全等 24、推论(AAS)有两角和其中一角的对边对应相等的两个三角形全等 25、边边边公理(SSS)有三边对应相等的两个三角形全等 26、斜边、直角边公理(HL)有斜边和一条直角边对应相等的两个直角三角形全等 27、定理1在角的平分线上的点到这个角的两边的距离相等 28、定理2到一个角的两边的距离相同的点,在这个角的平分线上 29、角的平分线是到角的两边距离相等的所有点的集合 30、等腰三角形的性质定理等腰三角形的两个底角相等(即等边对等角) 31、推论1等腰三角形顶角的平分线平分底边并且垂直于底边 32、等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合 33、推论3等边三角形的各角都相等,并且每一个角都等于60° 34、等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边) 35、推论1三个角都相等的三角形是等边三角形 36、推论2有一个角等于60°的等腰三角形是等边三角形 37、在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半 38、直角三角形斜边上的中线等于斜边上的一半 39、定理线段垂直平分线上的点和这条线段两个端点的距离相等 40、逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上 41、线段的垂直平分线可看作和线段两端点距离相等的所有点的集合 42、定理1关于某条直线对称的两个图形是全等形
初中平面几何145个知识点 几何要想取得好成绩,几何公式一定要烂熟于胸。几何公式是做好几何题的根基,因此同学们一定要在几何公式上多下功夫。 线 1 过两点有且只有一条直线 2 两点之间线段最短 3 同角或等角的补角相等 4 同角或等角的余角相等 … 5 过一点有且只有一条直线和已知直线垂直 6 直线外一点与直线上各点连接的所有线段中,垂线段最短 7 平行公理经过直线外一点,有且只有一条直线与这条直线平行 8 如果两条直线都和第三条直线平行,这两条直线也互相平行初中几何公式: 角 9 同位角相等,两直线平行 10 内错角相等,两直线平行 11 同旁内角互补,两直线平行 ? 12 两直线平行,同位角相等 13 两直线平行,内错角相等 14 两直线平行,同旁内角互补 初中几何公式:三角形 15 定理三角形两边的和大于第三边 16 推论三角形两边的差小于第三边 17 三角形内角和定理三角形三个内角的和等于180° 18 推论1 直角三角形的两个锐角互余 ] 19 推论2 三角形的一个外角等于和它不相邻的两个内角的和 20 推论3 三角形的一个外角大于任何一个和它不相邻的内角 21 全等三角形的对应边、对应角相等 22 边角边公理有两边和它们的夹角对应相等的两个三角形全等 23 角边角公理有两角和它们的夹边对应相等的两个三角形全等 24 推论有两角和其中一角的对边对应相等的两个三角形全等 25 边边边公理有三边对应相等的两个三角形全等 26 斜边、直角边公理有斜边和一条直角边对应相等的两个直角三角形全等 } 27 定理1 在角的平分线上的点到这个角的两边的距离相等 28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上 29 角的平分线是到角的两边距离相等的所有点的集合
目录 将军饮马模型 (3) 模型1:直线与两定点 (3) 模型2/角与定点 (10) 模型3两定点一定长 (15) 第十二章辅助圆 (20) 模型1 共端点,等线段模型 (20) 模型2 直角三角形共斜边模型 (23) 半角模型 (32) 模型实例 (33) 8字模型与飞镖模型 (50) 模型1:角的8字模型 (50) 模型2:角的飞镖模型 (54) 模型3 边的“8”字模型 (57) 模型4 边的飞镖模型 (58) 中点四大模型 (63) 模型1 倍长中线或类中线(与中点有关的线段)构造全等三角形 (63) 模型2 已知等腰三角形底边中点,可以考虑与顶点连接用“三线合一”. (66) 模型3 已知三角形一边的中点,可考虑中位线定理 (71) 模型4 已知直角三角形斜边中点,可以考虑构造斜边中线 (78) 二次函数 (85) 圆中的辅助线 (91) 模型1 连半径构造等腰三角形 (91) 模型2 构造直角三角形 (94) 模型3 与圆的切线有关的辅助线 (100) 相似模型 (111) 模型1:A、8模型 (111) 模型2 共边共角型 (116) 模型3 一线三等角型 (121) 模型4 倒数型 (127) 模型5 与圆有关的简单相似 (132) 模型6 相似和旋转 (136) 1.2空间几何体的三视图和直观图 (145)
1.3 空间几何体的表面积与体积 (145) 手拉手模型 (147) 模型手拉手 (147) 三垂直全等模型 (158) 模型三垂直全等模型 (158) 蚂蚁行程 (170) 模型立体图形展开的最短路径 (170) 截长补短辅助线模型 (180) 模型:截长补短 (180) 角平分线四大模型 (192) 模型1 角平分线的点向两边作垂线 (192) 模型2 截取构造对称全等 (194) 模型3 角平分线+垂线构造等腰三角形 (198) 模型4 角平分线+平行线 (200)
初中数学九大几何模型 一、手拉手模型----旋转型全等 (1)等边三角形 【条件】:△OAB 和△OCD 均为等边三角形; 【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED (2)等腰直角三角形 【条件】:△OAB 和△OCD 均为等腰直角三角形; 【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED (3)顶角相等的两任意等腰三角形 【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB 【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AED O A B C D E 图 1 O A B C D E 图 2 O A B C D E 图 1 O A C D E 图 2 O A B C D E O A B C D E 图 1 图 2
二、模型二:手拉手模型----旋转型相似 (1)一般情况 【条件】:CD ∥AB , 将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况 【条件】:CD ∥AB ,∠AOB=90° 将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ; ③ ===OA OB OC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有22 22CD AB B C AD +=+;⑥BD AC 21 S △BCD ?= 三、模型三、对角互补模型 (1)全等型-90° 【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB 【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 2 1 S S S =+= 证明提示: ①作垂直,如图2,证明△CDM ≌△CEN ②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ; ③2△OCD △OCE OC 21 S S =- O B C O A C D E O B C D E O A C D A O B C D E 图 1 A O B C D E M N 图 2 A O B C D E F 图 3 A O B C D E M N 图 4
1 过两点有且只有一条直线 2 两点之间线段最短 3 同角或等角的补角相等 4 同角或等角的余角相等 5 过一点有且只有一条直线和已知直线垂直 6 直线外一点与直线上各点连接的所有线段中,垂线段最短 7 平行公理经过直线外一点,有且只有一条直线与这条直线平行 8 如果两条直线都和第三条直线平行,这两条直线也互相平行 9 同位角相等,两直线平行 10 内错角相等,两直线平行 11 同旁内角互补,两直线平行 12两直线平行,同位角相等 13 两直线平行,内错角相等 14 两直线平行,同旁内角互补 15 定理三角形两边的和大于第三边 16 推论三角形两边的差小于第三边 17 三角形内角和定理三角形三个内角的和等于180° 18 推论1 直角三角形的两个锐角互余 19 推论2 三角形的一个外角等于和它不相邻的两个内角的和 20 推论3 三角形的一个外角大于任何一个和它不相邻的内角 21 全等三角形的对应边、对应角相等 22边角边公理(SAS) 有两边和它们的夹角对应相等的两个三角形全等23 角边角公理( ASA)有两角和它们的夹边对应相等的两个三角形全等
24 推论(AAS) 有两角和其中一角的对边对应相等的两个三角形全等 25 边边边公理(SSS) 有三边对应相等的两个三角形全等 26 斜边、直角边公理(HL) 有斜边和一条直角边对应相等的两个直角三角形全等 27 定理1 在角的平分线上的点到这个角的两边的距离相等 28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上 29 角的平分线是到角的两边距离相等的所有点的集合 30 等腰三角形的性质定理等腰三角形的两个底角相等 (即等边对等角) 31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边 32 等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合 33 推论3 等边三角形的各角都相等,并且每一个角都等于60° 34 等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边) 35 推论1 三个角都相等的三角形是等边三角形 36 推论 2 有一个角等于60°的等腰三角形是等边三角形 37 在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半 38 直角三角形斜边上的中线等于斜边上的一半 39 定理线段垂直平分线上的点和这条线段两个端点的距离相等 40 逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上 41 线段的垂直平分线可看作和线段两端点距离相等的所有点的集合 42 定理1 关于某条直线对称的两个图形是全等形 43 定理 2 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线 44定理3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上
角平分线四大模型 模型1 角平分线的点向两边作垂线 如图,P是∠MON的平分线上一点,过点P作PA⊥OM于点A,PB⊥ON于点B,则PB=PA 模型分析 利用角平分线的性质:角平分线上的点到角两边的距离相等,构造模型,为边相等、角相等、三角形全等创造更多的条件,进而可以快速找到解题的突破口 模型实例 (1)如图①,在△ABC中,∠C=90°,AD平分∠CAB,BC=6,BD=4,那么点D到直线AB的距离是 解答:如图,过点D作DE⊥AB于点E,∵AD平分∠CAB,∴CD=DE. ∵CB=6,BD=4,∴DE=CD=2,即点D到直线AB的距离是2. (2)如图②,∠1=∠2,∠3=∠4,求证:AP平分∠BAC 证明:如图,过点P作PD⊥AB于点D,PE⊥BC于点E,PF⊥AC于点F, ∵∠1=∠2,∴PD=PE,∵∠3=∠4, ∴PE=PF,∴PD=PF 又∵PD⊥AB,PF⊥AC,∴AP平分∠BAC(角平分线的判定)
练习 1、如图,在四边形ABCD中,BC>AB,AD=DC,BD平分∠ABC , 求证:∠BAD+∠BCD=180° 证明:作DE⊥BC于E,作DF⊥BA的延长线于F,∴∠F=∠DEC=90°, ∵BD平分∠ABC,∴DF=DE,又∵AD=DC,∴△DFA≌DEC,∴∠FAD=∠C ∵∠FAD+∠BAD=180°,∴∠BAD+∠BCD=180° 2.如图,△ABC的外角∠ACD∠的平分线CP与内角∠ABC的平分线BP相交于点P,若∠BPC=40°,则∠CAP=. 解答:如图所示,作PN⊥BD于N,作PF⊥BA,交BA延长线于F,作PM⊥AC于M ∵BP、CP分别是∠CBA和∠DCA的角平分线,∴∠ABP=∠CBP,∠DCP=∠ACP, PF=PN=PM,∵∠BAC=∠ACD-∠ABC,∠BPC=∠PCD-∠PBC(外角性质) ∴∠BAC=2∠PCD-2∠PBC=2(∠PCD-∠PBC)=2∠BPC=80° ∴∠CAF=180°-∠BAC=100°,∵PF=PM ∴AP是∠FAC的角平分线,∴∠CAP=∠PAF=50° 模型2 截取构造对称全等 如图,P是∠MON的平分线上的一点,点A是射线OM上任意一点,在ON上截取OB=OA,连接PB,则△OPB≌△OPA 模型分析
C D A B F E C D 初中几何经典模型 【模型介绍】 手拉手模型: 1、 【条件】 如图两个等边三角形ABD ?与BCE ?,连结 AE 与CD , 【结论】(1)DBC ABE ??? (2)DC AE = (3)AE 与DC 之间的夹角为?60 (4)AE 与DC 的交点设为H , BH 平分AHC ∠ 2、 【条件】如图两个等腰直角三角形ADC 与EDG ,连结CE AG ,,二者相交于点H 。 【结论】 (1)CDE ADG ???是否成立? (2)AG =CE (3)AG 与CE 之间的夹角为 90 (4)HD 是否平分AHE ∠? 旋转模型: 一、邻角相等对角互补模型 【条件】如图,四边形ABCD 中,AB =AD ,90BAD BCD ?∠=∠= 【结论】45ACB ACD BC CD ?∠=∠=+=① ②
二、角含半角模型:全等 角含半角要旋转:构造两次全等 【条件】:如图,点分别是正方形的边上的点,,连接; 【结论】(1)AFE AGE △△? (2) ; 一线三等角模型: 【条件】 一条直线同一侧三个相等的角(如图); 【结论】CDE ABC ∽△△ 1、锐角形一线三等角 2、直角形一线三等角 F E D C B A G F E D C B A A B C D E A B C D E F E F 、ABCD BC CD 、45EAF ∠=?EF EF BE FD = +
3、钝角形一线三等角 【真题拾遗】 1.(2014?广州)如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O,设AB=a,CG=b(a>b).下列结论:①△BCG≌△DCE;②BG⊥DE;③=;④(a﹣b)2?S△EFO=b2?S△DGO.其中结论正确的个数是() A.4个B.3个C.2个D.1个2.(2016?广州)如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论: ①四边形AEGF是菱形②△AED≌△GED ③∠DFG=112.5°④BC+FG=1.5 其中正确的结论是.
初中数学公式 大全
a b a b = ? ? - a (a < 0) 初中数学定理、公式汇编 一、数与代数 1. 数与式 (1) 实数 实数的性质: 1 ①实数 a 的相反数是—a ,实数 a 的倒数是 (a≠0); a ②实数 a 的绝对值: ?a (a > 0) ? a ?0(a = 0) ?- a (a < 0) ③正数大于 0,负数小于 0,两个负实数,绝对值大的反而小。二次根式: ①积与商的方根的运算性质: = ? (a≥0,b≥0); = (a≥0,b >0); ②二次根式的性质: = a = ?a (a ≥ 0) ? (2)整式与分式 ①同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,即 a m ? a n = a m +n (m 、n 为正整数); ②同底数幂的除法法则:同底数幂相除,底数不变,指数相减,即 a m ÷ a n = a m -n (a≠0,m 、n 为正整数,m>n ); ③幂的乘方法则:幂的乘方,底数不变,指数相乘,即(ab )n = a n b n (n 为正 整数); ④零指数: a 0 = 1 (a≠0); ab a b a 2
- b + b 2 - 4ac ± ⑤负整数指数: a -n = 1 a n (a≠0,n 为正整数); ⑥平方差公式:两个数的和与这两个数的差的积等于这两个数的平方,即 (a + b )(a - b ) = a 2 - b 2 ; ⑦完全平方公式:两数和(或差)的平方,等于它们的平方和,加上(或减去) 它们的积的 2 倍,即(a ± b )2 = a 2 ± 2ab + b 2 ; 分式 ①分式的基本性质:分式的分子和分母都乘以(或除以)同一个不等于零的整 a 式,分式的值不变,即 b = a ? m ; a b ? m b a c ac = a ÷ m b ÷ m ,其中 m 是不等于零的代数式; ②分式的乘法法则: ? = ; b d bd a c a d ad ③分式的除法法则: ÷ b d = ? = b c (c ≠ 0) ; bc ④分式的乘方法则: ( a b )n = a b n a b (n 为正整数); a ± b ⑤同分母分式加减法则: ± = ; c c c a d ⑥异分母分式加减法则: c b 2. 方程与不等式 = ab ± cd ; bc ①一元二次方程 ax 2 + bx + c = 0 (a≠0)的求根公式: x = (b 2 2a - 4ac ≥ 0) ②一元二次方程根的判别式: ? = b 2 - 4ac 叫做一元二次方程 ax 2 + bx + c = 0 (a≠0)的根的判别式: ? > 0 ? 方程有两个不相等的实数根; ? = 0 ? 方程有两个相等的实数根; ? < 0 ? 方程没有实数根; ③一元二次方程根与系数的关系:设 x 1 、 x 2 是方程 ax 2 + bx + c = 0 n