回溯算法1

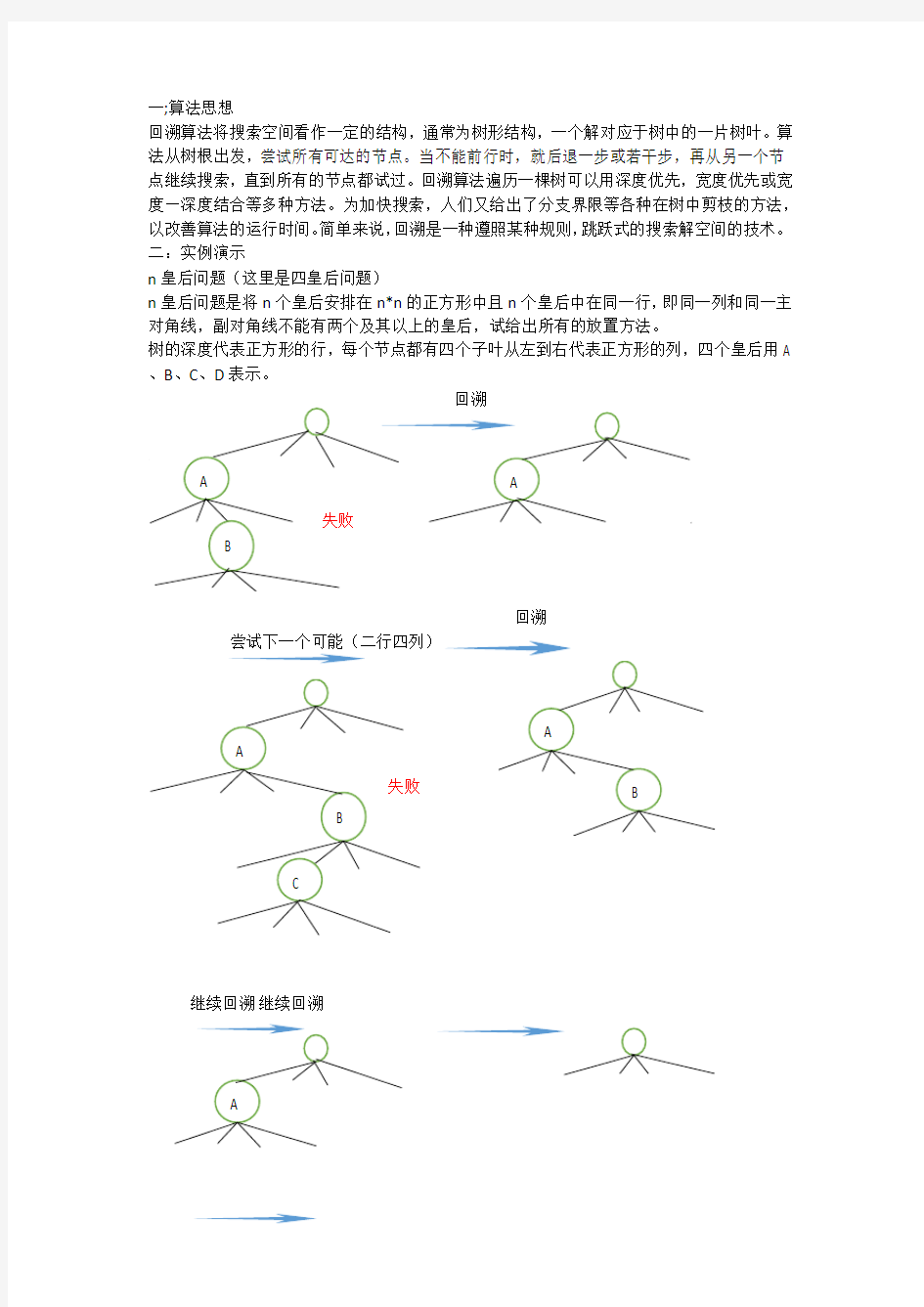
一;算法思想

回溯算法将搜索空间看作一定的结构，通常为树形结构，一个解对应于树中的一片树叶。算法从树根出发，尝试所有可达的节点。当不能前行时，就后退一步或若干步，再从另一个节点继续搜索，直到所有的节点都试过。回溯算法遍历一棵树可以用深度优先，宽度优先或宽度—深度结合等多种方法。为加快搜索，人们又给出了分支界限等各种在树中剪枝的方法，以改善算法的运行时间。简单来说，回溯是一种遵照某种规则，跳跃式的搜索解空间的技术。 二：实例演示

n 皇后问题（这里是四皇后问题）

n 皇后问题是将n 个皇后安排在n*n 的正方形中且n 个皇后中在同一行，即同一列和同一主对角线，副对角线不能有两个及其以上的皇后，试给出所有的放置方法。

树的深度代表正方形的行，每个节点都有四个子叶从左到右代表正方形的列，四个皇后用A 、B 、C 、D 表示。

回溯

尝试下一个可能（二行四列）

继续回溯 继续回溯

子集和数的回溯算法

设计四 子集和数的回溯算法 班级通信08-2BF 学号1408230929 姓名杨福 成绩 分 一、 设计目的 1.掌握回溯法解题的基本思想； 2.掌握子集和数问题的回溯算法； 3.进一步掌握子集和数问题的回溯递归算法、迭代算法的基本思想和算法设计方法； 二、 设计内容 a) 任务描述 1）子集和数问题简介 子集和数问题是假定有n 个不同的正数（通常称为权），要求找出这些数中所有事的某和数为M 的组合。 2）设计任务简介 设计、编程、测试求解子集和数问题的回溯算法。 1． 子集和数问题的表示方案 本设计利用大小固定的元组来研究回溯算法，在此情况下，解向量的元素X （i ）取1或0值，它表示是否包含了权数W （i ）. 生成图中任一结点的儿子是很容易的。对于i 级上的一个结点，其左儿子对应于X （i ）=1，右儿子对应于X(i)=0。对于限界函数的 一种简单选择是，当且仅当∑∑+==≥+ n k i k i M i W i X i W 11)()()(时，B(X(1),〃〃〃，X （k ）)=true 。 显然，如果这个条件不满足，X(1),〃〃〃，X （k ）就不能导致一个答案结点。如果假定这些W （i ）一开始就是按非降次序列排列的，那么这些限界函数可以被强化。在这种情 况下，如果M k W i X i W k i >++∑=)1()()(1 ,则X(1),〃〃〃，X （k ）就不能导致一个答案结 点。因此，将要使用的限界函数是B k （X （1），〃〃〃，X （k ））=true,当且仅当 M i W i X i W n k i k i =+∑∑+==11)()()(。 2． 主要数据类型与变量 int M ; // 表示要求得到的子集和； int s; // 表示所选当前元素之前所选的元素和；

算法设计与分析复习题目及答案

一。选择题 1、二分搜索算法是利用（ A ）实现的算法。 A、分治策略 B、动态规划法 C、贪心法 D、回溯法 2、下列不是动态规划算法基本步骤的是（ B ）。 A、找出最优解的性质 B、构造最优解 C、算出最优解 D、定义最优解 3、最大效益优先是（ A ）的一搜索方式。 A、分支界限法 B、动态规划法 C、贪心法 D、回溯法 4、在下列算法中有时找不到问题解的是（ B ）。 A、蒙特卡罗算法 B、拉斯维加斯算法 C、舍伍德算法 D、数值概率算法 5. 回溯法解旅行售货员问题时的解空间树是（ B ）。 A、子集树 B、排列树 C、深度优先生成树 D、广度优先生成树6．下列算法中通常以自底向上的方式求解最优解的是（ B ）。 A、备忘录法 B、动态规划法 C、贪心法 D、回溯法 7、衡量一个算法好坏的标准是（C ）。 A 运行速度快 B 占用空间少 C 时间复杂度低 D 代码短 8、以下不可以使用分治法求解的是（D ）。 A 棋盘覆盖问题 B 选择问题 C 归并排序 D 0/1背包问题 9. 实现循环赛日程表利用的算法是（ A ）。 A、分治策略 B、动态规划法 C、贪心法 D、回溯法 10、下列随机算法中运行时有时候成功有时候失败的是（C ） A 数值概率算法 B 舍伍德算法 C 拉斯维加斯算法 D 蒙特卡罗算法 11．下面不是分支界限法搜索方式的是（ D ）。 A、广度优先 B、最小耗费优先 C、最大效益优先 D、深度优先12．下列算法中通常以深度优先方式系统搜索问题解的是（ D ）。 A、备忘录法 B、动态规划法 C、贪心法 D、回溯法 13.备忘录方法是那种算法的变形。（ B ）

回溯搜索算法

补充2 回溯法 解回溯法的深度优先搜索策略 z理解回溯法的深度优先搜索策略。 z掌握用回溯法解题的算法框架 （1）递归回溯 （2）迭代回溯 （3）子集树算法框架 （4）排列树算法框架 通过应用范例学习回溯法的设计策略 z通过应用范例学习回溯法的设计策略。

Sch2-1z Sch2-1 方法概述搜索算法介绍 （1）穷举搜索 （2）盲目搜索 —深度优先(DFS)或回溯搜索( Backtracking); —广度优先搜索( BFS ); (Branch &Bound) —分支限界法(Branch & Bound)；—博弈树搜索( α-βSearch) （3）启发式搜索 —A* 算法和最佳优先( Best-First Search ) —迭代加深的A*算法 —B*AO*SSS*等算法B , AO , SSS 等算法 —Local Search, GA等算法

Sch2-1z Sch2-1 方法概述搜索空间的三种表示： —表序表示：搜索对象用线性表数据结构表示； —显示图表示：搜索对象在搜索前就用图（树）的数据结构表示； —隐式图表示：除了初始结点，其他结点在搜索过程中动态生成。缘于搜索空间大，难以全部存储。 z 搜索效率的思考：随机搜索 —上世纪70年代中期开始，国外一些学者致力于研究随机搜索求解困难的组合问题，将随机过程引入搜索； —选择规则是随机地从可选结点中取一个从而可以从统计角度分析搜选择规则是随机地从可选结点中取一个，从而可以从统计角度分析搜索的平均性能； —随机搜索的一个成功例子是：判定一个很大的数是不是素数，获得了第个多式时算法 第一个多项式时间的算法。

回溯算法的应用(DOC)

回溯算法的应用 课程名称：算法设计与分析 院系：************************ 学生姓名：****** 学号：************ 专业班级：***************************** 指导教师：****** 2013年12月27日

回溯法的应用 摘要：回溯法（探索与回溯法）是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。 回溯法，其意义是在递归直到可解的最小问题后，逐步返回原问题的过程。而这里所说的回溯算法实际是一个类似枚举的搜索尝试方法，它的主题思想是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。 回溯算法是尝试搜索算法中最为基本的一种算法，其采用了一种“走不通就掉头”的思想，作为其控制结构。在包含问题的所有解的解空间树中，按照深度优先搜索的策略，从根结点出发深度探索解空间树。当探索到某一结点时，要先判断该结点是否包含问题的解，如果包含，就从该结点出发继续探索下去，如果该结点不包含问题的解，则逐层向其祖先结点回溯。若用回溯法求问题的所有解时，要回溯到根，且根结点的所有可行的子树都要已被搜索遍才结束。而若使用回溯法求任一个解时，只要搜索到问题的一个解就可以结束。 全排列和求最优解问题是比较经典的问题，我们可以采用多种算法去求解此问题，比如动态规划法、分支限界法、回溯法。在这里我们采用回溯法来解决这个问题。 关键词：回溯法全排列最优值枚举

算法分析与程序设计动态规划及回溯法解背包问题

动态规划法、回溯法解0-1背包问题 2012级计科庞佳奇 一、问题描述与分析 1.动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中，可能会 有许多可行解。每一个解都对应于一个值，我们希望找到具有最优值的解。动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。若用分治法来解这类问题，则分解得到的子问题数目太多，有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，节省时间。我们可以用一个表来记录所有已解的子问题的答案。 不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。这就是动态规划法的基本思路。具体的动态规划算法多种多样，但它们具有相同的填表格式。 多阶段决策问题中，各个阶段采取的决策，一般来说是与时间有关的，决策依赖于当前状态，又随即引起状态的转移，一个决策序列就是在变化的状态中产生出来的，故有“动态”的含义，称这种解决多阶段决策最优化问题的方法为动态规划方法。任何思想方法都有一定的局限性，超出了特定条件，它就失去了作用。同样，动态规划也并不是万能的。适用动态规划的问题必须满足最优化原理和无后效性。1.最优化原理（最优子结构性质）最优化原理可这样阐述：一个最优化策略具有这样的性质，不论过去状态和决策如何，对前面的决策所形成的状态而言，余下的诸决策必须构成最优策略。简而言之，一个最优化策略的子策略总是最优的。一个问题满足最优化原理又称其具有最优子结构性质。2.无后效性将各阶段按照一定的次序排列好之后，对于某个给定的阶段状态，它以前各阶段的状态无法直接影响它未来的决策，而只能通过当前的这个状态。换句话说，每个状态都是过去历史的一个完整总结。这就是无后向性，又称为无后效性。3.子问题的重叠性动态规划将原来具有指数级时间复杂度的搜索算法改进成了具有多项式时间复杂度的算法。其中的关键在于解决冗余，这是动态规划算法的根本目的。动态规划实质上是一种以空间换时间的技术，它在实现的过程中，不得不存储产生过程中的各种状态，所以它的空间复杂度要大于其它的算法。 01背包是在M件物品取出若干件放在空间为W的背包里，每件物品的体积为W1，W2……Wn，与之相对应的价值为P1,P2……Pn。求出获得最大价值的方案。 2.回溯法（探索与回溯法）是一种选优搜索法，按选优条件向前搜索，以达到目 标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。 在包含问题的所有解的解空间树中，按照深度优先搜索的策略，从根结点出发深度探索解空间树。当探索到某一结点时，要先判断该结点是否包含问题的解，如果包含，就从该结点出发继续探索下去，如果该结点不包含问题的解，则逐层向其祖先结点回溯。（其实回溯法就是对隐式图的深度优先搜索算法）。若用回溯法求问题的所有解时，要回溯到根，且根结点的所有可行的子树都要已被搜索遍才结束。

搜索与回溯算法介绍

搜索与回溯算法介绍 一、概述： 计算机常用算法大致有两大类：一类叫蛮干算法，一类叫贪心算法。前者常使用的手段就是搜索，对全部解空间进行地毯式搜索，直到找到指定解或最优解。后者在求最优解问题的过程中，依据某种贪心标准，从问题的初始状态出发，直接去求每一步的最优解，通过若干次的贪心选择，最终得出整个问题的最优解。 二、搜索与回溯： 这里着重介绍搜索与回溯。当很多问题无法根据某种确定的计算法则来求解时可以利用搜索与回溯的技术求解。回溯是搜索算法中既带有系统性又带有跳跃性的一种控制策略。它的基本思想是：为了求得问题的解，先选择某一种可能情况向前探索。在探索过程中，一旦发现原来的选择是错误的，就退回一步重新选择，然后继续向前探索，如此反复进行，直至得到解或证明无解。如迷宫问题：进入迷宫后，先随意选择一个前进方向，一步步向前试探前进。如果碰到死胡同，说明前进方向已无路可走，这时，首先看其它方向是否还有路可走，如果有路可走，则沿该方向再向前试探；如果已无路可走，则返回一步，再看其它方向是否还有路可走；如果有路可走，则沿该方向再向前试探。按此原则不断搜索回溯再搜索，直到找到新的出路或从原路返回入口处无解为止。 【建立解空间】 问题的解应该如何描述，如何建立呢？问题的解空间：应用回溯法解问题时，首先应明确定义问题的解空间。问题的解空间应到少包含问题的一个（最优）解。借助图论的思想，可以用图来描述，图的定义为G，由顶点集和边集构成，顶点即实实在在的数据、对象，而边可以抽象为关系，即顶点间的关系，这种关系不一定非要在数据结构上表现出来，用数据结构的语言来描述，如果关系是一对一，则为线性表，如果关系是一对多，则为树，如果关系是多对多，则为图，如果完全没有关系，则为集合。但在数据结构中这种关系不一定非要在数据的存储性质上一开始就表现出来，譬如，你可以用一个数组表示一个线性表，也可以表示完全二叉树，同样也可以用邻接表表示一个图，对于关系的描述不是数据结构本身的描述，而是算法的描述，正如数据结构是离不开特定的算法一样，不可分开单独而谈。 确定了解空间的组织结构后，回溯法就从开始结点（根结点）出发，以深度优先的方式搜索整个解空间。这个开始结点就成为一个活结点，同时也成为当前的扩展结点。在当前的扩展结点处，搜索向纵深方向移至一个新结点。这个新结点就成为一个新的活结点，并成为当前扩展结点。如果在当前的扩展结点处不能再向

回溯算法之0-1背包问题

1、实验目的 （1）掌握回溯法设计策略。 （2）通过0-1背包问学习回溯法法设计技巧2.实验内容 源程序： #include using namespace std; double c;//背包容量 int n; //物品数 double w[100];//物品重量数组 double p[100];//物品价值数组 double cw=0;//当前重量 double cp=0;//当前价值 double bestp=0;//当前最优值 double bound(int i) { double cleft,b; //计算上界 cleft=c-cw;//剩余容量 b=cp; //以物品单位重量价值递减序装入物品 while(i<=n&&w[i]<=cleft) { cleft-=w[i]; b+=p[i]; i++; } //装满背包 if(i<=n) b+=p[i]*cleft/w[i]; return b; } void Backtrack(int i) { if(i>n) { if(cp>bestp) bestp=cp; return;

} if(cw+w[i]<=c) //搜索左子树 { cw+=w[i]; cp+=p[i]; Backtrack(i+1); cp-=p[i]; cw-=w[i]; } if(bound(i+1)>bestp)//搜索右子树 Backtrack(i+1); } double Knapsack (double pp[],double ww[],double d) { int i; double TP=0,TW=0; cw=0.0;cp=0.0;bestp=0.0;//计算所有物品的重量及价值 for(i=1;i<=n;i++) { TP=TP+pp[i]; TW=TW+ww[i]; } if(TW<=d)//所有物品装入背包 bestp=TP; else { Backtrack(1); } return bestp; }; int main() {

算法设计与分析：回溯法-实验报告

应用数学学院信息安全专业班学号姓名 实验题目回溯算法 实验评分表

实验报告 一、实验目的与要求 1、理解回溯算法的基本思想； 2、掌握回溯算法求解问题的基本步骤； 3、了解回溯算法效率的分析方法。 二、实验内容 【实验内容】 最小重量机器设计问题：设某一个机器有n个部件组成，每个部件都可以m个不同供应商处购买，假设已知表示从j个供应商购买第i个部件的重量，表示从j个供应商购买第i个部件的价格，试用回溯法求出一个或多个总价格不超过c且重量最小的机器部件购买方案。 【回溯法解题步骤】 1、确定该问题的解向量及解空间树； 2、对解空间树进行深度优先搜索； 3、再根据约束条件（总价格不能超过c）和目标函数（机器重量最小）在搜索过程中剪去多余的分支。 4、达到叶结点时记录下当前最优解。 5、实验数据n,m, ] ][ [j i w,] ][ [j i c的值由自己假设。 三、算法思想和实现【实现代码】

【实验数据】 假设机器有3个部件，每个部件可由3个供应商提供（n=3，m=3）。总价不超过7（c<=7）。 部件重量表： 部件价格表： 【运行结果】

实验结果：选择供应商1的部件1、供应商1的部件2、供应商3的部件3，有最小重量机器的重量为4，总价钱为6。 四、问题与讨论 影响回溯法效率的因素有哪些？ 答：影响回溯法效率的因素主要有以下这五点： 1、产生x[k]的时间； 2、满足显约束得x[k]值的个数； 3、计算约束函数constraint的时间； 4、计算上界函数bound的时间； 5、满足约束函数和上界函数约束的所有x[k]的个数。 五、总结 这次实验的内容都很有代表性，通过上机操作实践与对问题的思考，让我更深层地领悟到了回溯算法的思想。 回溯算法的基本思路并不难理解，简单来说就是：从一条路往前走，能进则进，不能进则退回来，换一条路再试。回溯法的基本做法是深度优先搜索，是一种组织得井井

回溯算法实验

中原工学院信息商务学院 实验报告 实验项目名称回溯划算法的应用 课程名称算法设计与分析 学院(系、部)中原工学院信息商务学院学科专业计算机科学与技术系班级学号计科132班17号姓名程一涵 任课教师邬迎 日期2014年12月9日

实验五回溯算法的应用 一、实验目的 1．掌握回溯算法的基本概念 2．熟练掌握回溯算法解决问题的基本步骤。 3．学会利用回溯算法解决实际问题。 二．问题描述 题目一：N皇后问题 要在n*n的国际象棋棋盘中放n个皇后，使任意两个皇后都不能互相吃掉。规则：皇后能吃掉同一行、同一列、同一对角线的任意棋子。求所有的解要求：键盘输入皇后的个数n (n ≤ 13) 输出有多少种放置方法 输入输出实例：

三．算法设计 首先，确定第一行皇后的位置，再确定第二行的位置，并且要注意不能同行同列同对角线，若是发现有错则返回上一层，继续判断。满足约束条件时，则开始搜索下一个皇后的位置，直到找出问题的解。 四.程序调试及运行结果分析 五.实验总结 通过这次试验，使得我们面对问题时的解题思路变得更加灵活和多变，并且使我们的编写能力稍稍的提高一些。初步了解了回溯算法，回溯算法实际是一个类似枚举的搜索尝试方法，他的主题思想是在搜索尝试的过程中寻找问题的解，当发现已不满足求解条件时，就回溯返回，尝试别的路径。他特别适用于求解那些涉及到寻求一组解的问题或者求满足某些约束条件的最优解的问题。此算法具有结构清晰，容易理解且可读性强等优点，并且通过稍加变通也可以适用于其他类似问题

附录：程序清单（程序过长，可附主要部分） #include #include using namespace std; int a[20],n; backdate(int n); int check(int k); void output(int n); int main() { int n; cout<<"请输入皇后的个数："; cin>>n; cout<<"位置排列是："<0) { a[k]=a[k]+1; while((a[k]<=n) && (check(k)==0)) a[k]=a[k]+1; if(a[k]<=n) if(k==n) { num++; output(n); } else { k=k+1; a[k]=0; } else k=k-1; } cout<<"一共有"<

回溯法

回溯法 回溯法也是搜索算法中的一种控制策略，但与枚举法不同的是，它是从初始状态出发，运用题目给出的条件、规则，按照深度优秀搜索的顺序扩展所有可能情况，从中找出满足题意要求的解答。回溯法是求解特殊型计数题或较复杂的枚举题中使用频率最高的一种算法。 一、回溯法的基本思路 何谓回溯法，我们不妨通过一个具体实例来引出回溯法的基本思想及其在计算机上实现的基本方法。【例题12.2.1】n皇后问题 一个ｎ×ｎ（1≤n≤100）的国际象棋棋盘上放置ｎ个皇后，使其不能相互攻击，即任何两个皇后都不能处在棋盘的同一行、同一列、同一条斜线上，试问共有多少种摆法？ 输入： n 输出： 所有分案。每个分案为n+1行，格式： 方案序号 以下n行。其中第i行（1≤i≤n）行为棋盘i行中皇后的列位置。 在分析算法思路之前，先让我们介绍几个常用的概念： 1、状态（state） 状态是指问题求解过程中每一步的状况。在ｎ皇后问题中，皇后所在的行位置i(1≤i≤n)即为其时皇后问题的状态。显然，对问题状态的描述，应与待解决问题的自然特性相似，而且应尽量做到占用空间少，又易于用算符对状态进行运算。 2、算符（operater） 算符是把问题从一种状态变换到另一种状态的方法代号。算符通常采用合适的数据来表示，设为局部变量。n皇后的一种摆法对应1．．ｎ排列方案（a1，…，a n）。排列中的每个元素a i对应ｉ行上皇后的列位置（1≤i≤n）。由此想到，在ｎ皇后问题中，采用当前行的列位置i(1≤i≤n)作为算符是再合适不过了。由于每行仅放一个皇后，因此行攻击的问题自然不存在了，但在试放当前行的一个皇后时，不是所有列位置都适用。例如(l，ｉ)位置放一个皇后，若与前1．．l-1行中的j行皇后产生对角线攻击(｜ｊ－l｜=｜a j －i｜)或者列攻击(ｉ≠a j)，那么算符ｉ显然是不适用的，应当舍去。因此，不产生对角线攻击和列攻击是ｎ皇后问题的约束条件，即排列（排列a1，…，a i，…，a j，…，a n）必须满足条件(｜ｊ－ｉ｜≠｜a j－a i｜) and (a i≠a j) (1≤i，j≤n)。 3、解答树（analytic tree） 现在让我们先来观察一个简单的ｎ皇后问题。设ｎ＝4，初始状态显然是一个空棋盘。 此时第一个皇后开始从第一行第一列位置试放，试放的顺序是从左至右、自上而下。每个棋盘由４个数据表征相应的状态信息（见下图）： （××××）

回溯算法实例一培训讲学

回溯算法实例一

【问题】填字游戏 问题描述：在3×3个方格的方阵中要填入数字1到N（N≥10）内的某9个数字，每个方格填一个整数，使得所有相邻两个方格内的两个整数之和为质数。试求出所有满足这个要求的各种数字填法。 可用试探发找到问题的解，即从第一个方格开始，为当前方格寻找一个合理的整数填入，并在当前位置正确填入后，为下一方格寻找可填入的合理整数。如不能为当前方格找到一个合理的可填证书，就要回退到前一方格，调整前一方格的填入数。当第九个方格也填入合理的整数后，就找到了一个解，将该解输出，并调整第九个的填入的整数，寻找下一个解。 为找到一个满足要求的9个数的填法，从还未填一个数开始，按某种顺序（如从小到大的顺序）每次在当前位置填入一个整数，然后检查当前填入的整数是否能满足要求。在满足要求的情况下，继续用同样的方法为下一方格填入整数。如果最近填入的整数不能满足要求，就改变填入的整数。如对当前方格试尽所有可能的整数，都不能满足要求，就得回退到前一方格，并调整前一方格填入的整数。如此重复执行扩展、检查或调整、检查，直到找到一个满足问题要求的解，将解输出。 回溯法找一个解的算法： { int m=0,ok=1; int n=8; do{ if (ok) 扩展; else 调整; ok=检查前m个整数填放的合理性; } while ((!ok||m!=n)&&(m!=0)) if (m!=0) 输出解; else 输出无解报告； } 如果程序要找全部解，则在将找到的解输出后，应继续调整最后位置上填放的整数，试图去找下一个解。相应的算法如下： 回溯法找全部解的算法： { int m=0,ok=1; int n=8; do{ if (ok) { if (m==n) { 输出解； 调整； } else 扩展; } else 调整; ok=检查前m个整数填放的合理性; } while (m!=0);

回溯算法实例一

【问题】填字游戏 问题描述：在3×3个方格的方阵中要填入数字1到N（N≥10）内的某9个数字，每个方格填一个整数，似的所有相邻两个方格内的两个整数之和为质数。试求出所有满足这个要求的各种数字填法。 可用试探发找到问题的解，即从第一个方格开始，为当前方格寻找一个合理的整数填入，并在当前位置正确填入后，为下一方格寻找可填入的合理整数。如不能为当前方格找到一个合理的可填证书，就要回退到前一方格，调整前一方格的填入数。当第九个方格也填入合理的整数后，就找到了一个解，将该解输出，并调整第九个的填入的整数，寻找下一个解。 为找到一个满足要求的9个数的填法，从还未填一个数开始，按某种顺序（如从小到大的顺序）每次在当前位置填入一个整数，然后检查当前填入的整数是否能满足要求。在满足要求的情况下，继续用同样的方法为下一方格填入整数。如果最近填入的整数不能满足要求，就改变填入的整数。如对当前方格试尽所有可能的整数，都不能满足要求，就得回退到前一方格，并调整前一方格填入的整数。如此重复执行扩展、检查或调整、检查，直到找到一个满足问题要求的解，将解输出。 回溯法找一个解的算法： { int m=0,ok=1; int n=8; do{ if (ok) 扩展; else 调整; ok=检查前m个整数填放的合理性; } while ((!ok||m!=n)&&(m!=0)) if (m!=0) 输出解; else 输出无解报告； } 如果程序要找全部解，则在将找到的解输出后，应继续调整最后位置上填放的整数，试图去找下一个解。相应的算法如下： 回溯法找全部解的算法： { int m=0,ok=1; int n=8; do{ if (ok) { if (m==n) { 输出解； 调整； } else 扩展; } else 调整; ok=检查前m个整数填放的合理性; } while (m!=0); }

实验四 回溯法的应用------跳马算法

实验四回溯法的应用------跳马算法 学号：012124345 姓名：梁文耀 一、实验目的 掌握使用回溯法求解问题的基本思路；理解其特点。 二、实验思想 算法的基本思路是： 定义结构体：struct PLACE{int x, int y}表示棋盘上的位置。 依题意，马每跳一步之后都可以从七个不同的方向选择下一步的跳马，当然，前提是跳的这一步在棋盘内且它前面的任何一步都没跳到这一格子上（限界），就可以认为这一步跳成功，否则跳马不成功。若跳马不成功，则找下一个方向尝试跳马，若七个方向都跳马不成功，则回溯。 假设棋盘的行（列）数为n。 在本算法中设置这样一个全局数组：c[8][2]={{2,1},{2,-1},{1,2},{1,-2},{-2,1},{-2,-1},{-1,2},{-1,-2}}; 来记录跳马的八个方向。 三、程序分析（主要算法） int map[12][12], status[12][12], kp; int start,finsh; int c[8][2]={{2,1},{2,-1},{1,2},{1,-2}, {-2,1},{-2,-1},{-1,2},{-1,-2}};

int flag = 0; void prt(int a[][12]) /* 打印棋盘状态*/ { int i,j; printf("\n"); for (i=2;i<=9;i++) { for (j=2;j<=9;j++) printf("%4d",a[i][j]); printf("\n"); } } void status2(void) /* 计算棋盘各点条件数*/ { int i,j,k,i2,j2,kz; for(i=0;i<12;i++) for(j=0;j<12;j++) status[i][j]=100; for(i=2;i<=9;i++) for(j=2;j<=9;j++) { kz=0;

实验五：01背包问题的回溯算法设计

实验五：0/1背包问题的回溯算法设计实验目的：0/1背包问题的回溯算法设计 实验原理：回溯算法设计。 实验要求：基本掌握回溯算法设计的原理方法。熟练掌握VC++中编程实现算法的常用技术和方法。 算法思想:0-1背包问题:给定n种物品和一背包.物品i的重量是wi,其价值为ui,背包的容量为C.问如何选择装入背包的物品,使得装入背包中物品的总价值最大? 分析: 0-1背包是子集合选取问题,一般情况下0-1背包是个NP问题.第一步确定解空间：装入哪几种物品 第二步确定易于搜索的解空间结构： 可以用数组p,w分别表示各个物品价值和重量。 用数组x记录，是否选种物品 第三步以深度优先的方式搜索解空间，并在搜索的过程中剪枝要求：（1）使用C++或TC2.0 （2）上机前要有源代码或流程图。#include using namespace std; class Knap { friend int Knapsack(int p[],int w[],int c,int n ); public: void print()

for(int m=1;m<=n;m++) { cout<

回溯算法

常用算法四（回溯算法） 1、概念 回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。 回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。 许多复杂的，规模较大的问题都可以使用回溯法，有“通用解题方法”的美称。 2、基本思想 在包含问题的所有解的解空间树中，按照深度优先搜索的策略，从根结点出发深度探索解空间树。当探索到某一结点时，要先判断该结点是否包含问题的解，如果包含，就从该结点出发继续探索下去，如果该结点不包含问题的解，则逐层向其祖先结点回溯。（其实回溯法就是对隐式图的深度优先搜索算法）。 若用回溯法求问题的所有解时，要回溯到根，且根结点的所有可行的子树都要已被搜索遍才结束。 而若使用回溯法求任一个解时，只要搜索到问题的一个解就可以结束。3、用回溯法解题的一般步骤： （1）针对所给问题，确定问题的解空间： 首先应明确定义问题的解空间，问题的解空间应至少包含问题的一个（最优）解。 （2）确定结点的扩展搜索规则 （3）以深度优先方式搜索解空间，并在搜索过程中用剪枝函数避免无效搜索。 4、算法应用示例：

八皇后问题的递归实现 [java]view plaincopy 1.public class Empress { 2. 3.private int n ; //皇后个数 4.private int[] x ; //当前解 5.private long sum ; //当前已找到的可行方案数 6.private static int h ; //记录遍历方案序数 7. 8.public Empress(){ 9.this.sum = 0 ; //初始化方案数为1，当回溯到最佳方案的时候，就自增1 10.this.n = 8 ; //求n皇后问题，由自己定义 11.this.x = new int[n+1]; //x[i]表示皇后i放在棋盘的第i行的第x[i] 列 12. h = 1 ; //这个是我额外定义的变量，用于遍历方案的个数，请看backTrace() 中h变量的作用，这里将它定义为static静态变量 13. } 14. 15.public boolean place (int k){ 16.for (int j = 1 ; j < k ; j++){ 17.//这个主要是刷选符合皇后条件的解，因为皇后可以攻击与之同一行同一列的 或同一斜线上的棋子 18.if ( (Math.abs(k - j)) == (Math.abs(x[j]-x[k])) || (x[j] == x [k]) ){ 19.return false ; //如果是与之同一行同一列的或同一斜线上的棋子， 返回false; 20. } 21. } 22.return true ;//如果不是与之同一行同一列的或同一斜线上的棋子，返回 true; 23. } 24. 25.public void backTrace (int t){ 26.if (t > n){ //当t>n时,算法搜索到叶节点，得到一个新的n皇后互不攻击放 置方案，方案数加1 27. sum ++ ; //方案数自增1 28. System.out.println ("方案" + (h++) + ""); 29. print(x); 30. System.out.print ("\n----------------\n");//华丽的分割线 31. }else { //当t<=n时，当前扩展的结点Z是解空间中的内部结点，该节点有 x[i]=1,2，…,n共n个子结点， 32.//对于当前扩展结点Z的每一个儿子结点，由place()方法检测其可行 性，

C语言设计之回溯算法

C语言设计之回溯算法（24点） 姚铸 问题叙述： 24点： 从键盘输入4个数字进行加减乘除，要求结果为24 输入要求 第一行：4 3 2 1 输出 24=12*2 2=2*1 12=4*3 问题分析：这个问题是我们小时候都应该玩过。问题的重点在于输入的数据要进行运算后得到24这个值是问题的难点。4个数之间无序的运算有很多种情况。用程序去实现24点，就需要4个数之间进行每一种的讨论。用穷举是能够计算出来的。但是时间复杂度值太大。 算法设计：这类型问题的解决方案重点在于4个数算出的结果如果不能在该步运算出24能否后悔还原会 上一次循环或递归。这里的后悔就联想到回溯算法。 算法思想：从算法设计得到了回溯算法。后悔正是回溯算法的中心思想。在得不到真正的结果的时候退回上一步。在结果计算的时候运用if或while语言对程序结束进行控制。 特殊测试：5 5 5 1 这组数据计算24点是成立的。在运算的过程中会出现小数。 参考程序（这是我自己写出的程序代码，经过测试没有问题。）： 递归算法实现回溯： #include int i=0; void dian(float a,float b,float c,float d,int j); /*回朔声明*/ void jia(float a,float b,float c,float d,int j) /*进行加的运算*/ {if ((a*b!=0)&&(j<4)&&(i!=1)) {dian(a+b,c,d,0,j+1); if (i==1) printf("%g=%g+%g\n",a+b,a,b);} } void jian(float a,float b,float c,float d,int j) /*进行减的运算*/ {if ((a*b!=0)&&(j<4)&&(i!=1)) {dian(a-b,c,d,0,j+1); dian(b-a,c,d,0,j+1); if (i==1) printf("%g=%g-%g\n",a-b,a,b);} } void cheng(float a,float b,float c,float d,int j) /*进行乘的运算*/ {if ((a*b!=0)&&(j<4)&&(i!=1))

回溯算法的一些例题

回溯算法 搜索与回溯是计算机解题中常用的算法，很多问题无法根据某种确定的计算法则来求解，可以利用搜索与回溯的技术求解。回溯是搜索算法中的一种控制策略。它的基本思想是：为了求得问题的解，先选择某一种可能情况向前探索，在探索过程中，一旦发现原来的选择是错误的，就退回一步重新选择，继续向前探索，如此反复进行，直至得到解或证明无解。如迷宫问题：进入迷宫后，先随意选择一个前进方向，一步步向前试探前进,如果碰到死胡同，说明前进方向已无路可走，这时，首先看其它方向是否还有路可走，如果有路可走，则沿该方向再向前试探；如果已无路可走，则返回一步，再看其它方向是否还有路可走；如果有路可走，则沿该方向再向前试探。按此原则不断搜索回溯再搜索，直到找到新的出路或从原路返回入口处无解为止。 递归回溯法算法框架[一] procedure Try(k:integer); begin for i:=1 to 算符种数 Do if 满足条件 then begin 保存结果 if 到目的地 then 输出解 else Try(k+1); 恢复：保存结果之前的状态{回溯一步} end; end; 递归回溯法算法框架[二] procedure Try(k:integer); begin if 到目的地 then 输出解 else for i:=1 to 算符种数 Do if 满足条件 then begin 保存结果 Try(k+1); end; end;

例 1：素数环：把从1到20这20个数摆成一个环，要求相邻的两个数的和是一个素数。【算法分析】非常明显，这是一道回溯的题目。从1 开始，每个空位有 20（19）种可能，只要填进去的数合法：与前面的数不相同；与左边相邻的数的和是一个素数。第 20个数还要判断和第1个数的和是否素数。 〖算法流程〗1、数据初始化； 2、递归填数： 判断第J种可能是否合法； A、如果合法：填数；判断是否到达目标（20个已填完）：是，打印结果；不是，递归填下一个； B、如果不合法：选择下一种可能； 【参考程序】 program z74;框架[一] var a:array[0..20]of byte; b:array[0..20]of boolean; total:integer; function pd(x,y:byte):boolean; var k,i:byte; begin k:=2; i:=x+y; pd:=false; while (k<=trunc(sqrt(i)))and(i mod k<>0) do inc(k); if k>trunc(sqrt(i)) then pd:=true; end; procedure print; var j:byte; begin inc(total);write('<',total,'>:'); for j:=1 to 20 do write(a[j],' '); writeln; end; procedure try(t:byte); var i:byte; begin for i:=1 to 20 do if pd(a[t-1],i)and b[i] then begin a[t]:=i; b[i]:=false; if t=20 then begin if pd(a[20],a[1]) then print;end

算法设计与分析---回溯实验报告

《算法设计与分析》实验报告实验三回溯法

3.迷宫问题 一天Luna在森林里探险的时候不小心走入了一个迷宫，迷宫可以看成是由n * n的格点组成，每个格点只有2种状态，. 和#，前者表示可以通行后者表示不能通行。同时当Luna处在某个格点时，她只能移动到东南西北(或者说上下左右)四个方向之一的相邻格点上，Luna想要从点A走到点B（不能走出迷宫）。如果起点或者终点有一个不能通行(为#)，则看成无法办到。 [输入] 第1行是测试数据的组数k，后面跟着k组输入。 每组测试数据的第1行是一个正整数n (1 <= n <= 100)，表示迷宫的规模是n * n 的。 接下来是一个n * n的矩阵，矩阵中的元素为. 或者#。 再接下来一行是4个整数ha, la, hb, lb，描述A处在第ha行, 第la列，B处在第hb 行, 第lb列。注意到ha, la, hb, lb全部是从0开始计数的。

1.八皇后问题 1.1解题思路 八皇后问题的解法，很简单的解法。通过回溯实现枚举。 对于当前行，尝试是否可在当前列放置皇后，然后进入下一行的尝试，同时尝试完毕以后，要将当前行回复（回溯），来进行下一次尝试。 到达最后一行的时候，即递归结束条件，打印结果即可。 1.2程序运行情况 1.3所有的皇后解 见附录。（毕竟92个解...） 1.4程序源码（含注释）

2. 24点问题 2.1 解题思路 这题虽然使用dfs很简单，但是有一点思维在里面。我很惭愧，自己没有想出来怎么如意的独立AC此题。 遇到的最大的问题——如何插入括号？枚举插入、和运算符一同排列都不靠谱。解决方法是：用同等的办法转化。每一次从待组合的是数字中，任取两个数，随机用运算符计算完毕后，再放回去。下一次计算，再次重复这个过程，可以等价为有括号的运算方式了。 遇到第二个问题——如何实现这种“任取两个数”的选择方式。这里就直接体现出了我个人能力的不足。居然没想到。尝试使用STL的set，但是没成功。这里借鉴了网上的AC 思路，我感到自己思维太僵硬。解决方法是——对于当前的运算状态中，用两个循环实现枚举两个数，计算为完毕以后，结果覆盖在数组序号小的那个数的位置，再将第二个数与最后一个数字交换即可进入下一个状态。回溯的时候，只需要回复小序号的数字的位置的值，以及再一次swap即可。（因为第二个数字只是swap却没有改变过内容）。 一个细节问题，就是加法和乘法是没有顺序的，减法和除法是有顺序的，以及除法要考虑0异常。一共是6次枚举即可。 2.2 测试样例 5 5 5 1 ans is YES 1 1 4 2 ans is :NO 2.3 程序运行情况 样例一：

回溯算法

五、回溯法 回溯法也称为试探法，该方法首先暂时放弃关于问题规模大小的限制，并将问题的候选解按某种顺序逐一枚举和检验。当发现当前候选解不可能是解时，就选择下一个候选解；倘若当前候选解除了还不满足问题规模要求外，满足所有其他要求时，继续扩大当前候选解的规模，并继续试探。如果当前候选解满足包括问题规模在内的所有要求时，该候选解就是问题的一个解。在回溯法中，放弃当前候选解，寻找下一个候选解的过程称为回溯。扩大当前候选解的规模，以继续试探的过程称为向前试探。 1、回溯法的一般描述 可用回溯法求解的问题P，通常要能表达为：对于已知的由n元组（x1，x2，…，xn）组成的一个状态空间E={（x1，x2，…，xn）∣xi∈Si ，i=1，2，…，n}，给定关于n元组中的一个分量的一个约束集D，要求E中满足D的全部约束条件的所有n元组。其中Si是分量xi 的定义域，且 |Si| 有限，i=1，2，…，n。我们称E中满足D的全部约束条件的任一n元组为问题P的一个解。 解问题P的最朴素的方法就是枚举法，即对E中的所有n元组逐一地检测其是否满足D的全部约束，若满足，则为问题P的一个解。但显然，其计算量是相当大的。 我们发现，对于许多问题，所给定的约束集D具有完备性，即i元组（x1，x2，…，xi）满足D中仅涉及到x1，x2，…，xi的所有约束意味着 j（jj。因此，对于约束集D具有完备性的问题P，一旦检测断定某个j元组（x1，x2，…，xj）违反D中仅涉及x1，x2，…，xj的一个约束，就可以肯定，以（x1，x2，…，xj）为前缀的任何n元组（x1，x2，…，xj，xj+1，…，xn）都不会是问题P的解，因而就不必去搜索它们、检测它们。回溯法正是针对这类问题，利用这类问题的上述性质而提出来的比枚举法效率更高的算法。 回溯法首先将问题P的n元组的状态空间E表示成一棵高为n的带权有序树T，把在E中求问题P的所有解转化为在T中搜索问题P的所有解。树T类似于检索树，它可以这样构造：设 Si中的元素可排成xi(1) ，xi(2) ，…，xi(mi-1) ，|Si| =mi，i=1，2，…，n。从根开始，让T的第I层的每一个结点都有mi个儿子。这mi个儿子到它们的双亲的边，按从左到右的次序，分别带权 xi+1(1) ，xi+1(2) ，…，xi+1(mi) ，i=0，1，2，…，n-1。照这种构造方式，E中的一个n元组（x1，x2，…，xn）对应于T中的一个叶子结点，T的根到这个叶子结点的路径上依次的n条边的权分别为x1，x2，…，xn，反之亦然。另外，对于任意的0≤i≤n-1，E中n元组（x1，x2，…，xn）的一个前缀I元组（x1，x2，…，xi）对应于T中的一个非叶子结点，T的根到这个非叶子结点的路径上依次的I条边的权分别为x1，x2，…，xi，反之亦然。特别，E 中的任意一个n元组的空前缀（），对应于T的根。 因而，在E中寻找问题P的一个解等价于在T中搜索一个叶子结点，要求从T的根到该叶子结点的路径上依次的n条边相应带的n个权x1，x2，…，xn满足约束集D的全部约束。在T 中搜索所要求的叶子结点，很自然的一种方式是从根出发，按深度优先的策略逐步深入，即依次搜索满足约束条件的前缀1元组（x1i）、前缀2元组（x1，x2）、…，前缀I元组（x1，x2，…，xi），…，直到i=n为止。 在回溯法中，上述引入的树被称为问题P的状态空间树；树T上任意一个结点被称为问题P 的状态结点；树T上的任意一个叶子结点被称为问题P的一个解状态结点；树T上满足约束集D的全部约束的任意一个叶子结点被称为问题P的一个回答状态结点，它对应于问题P的一个解。