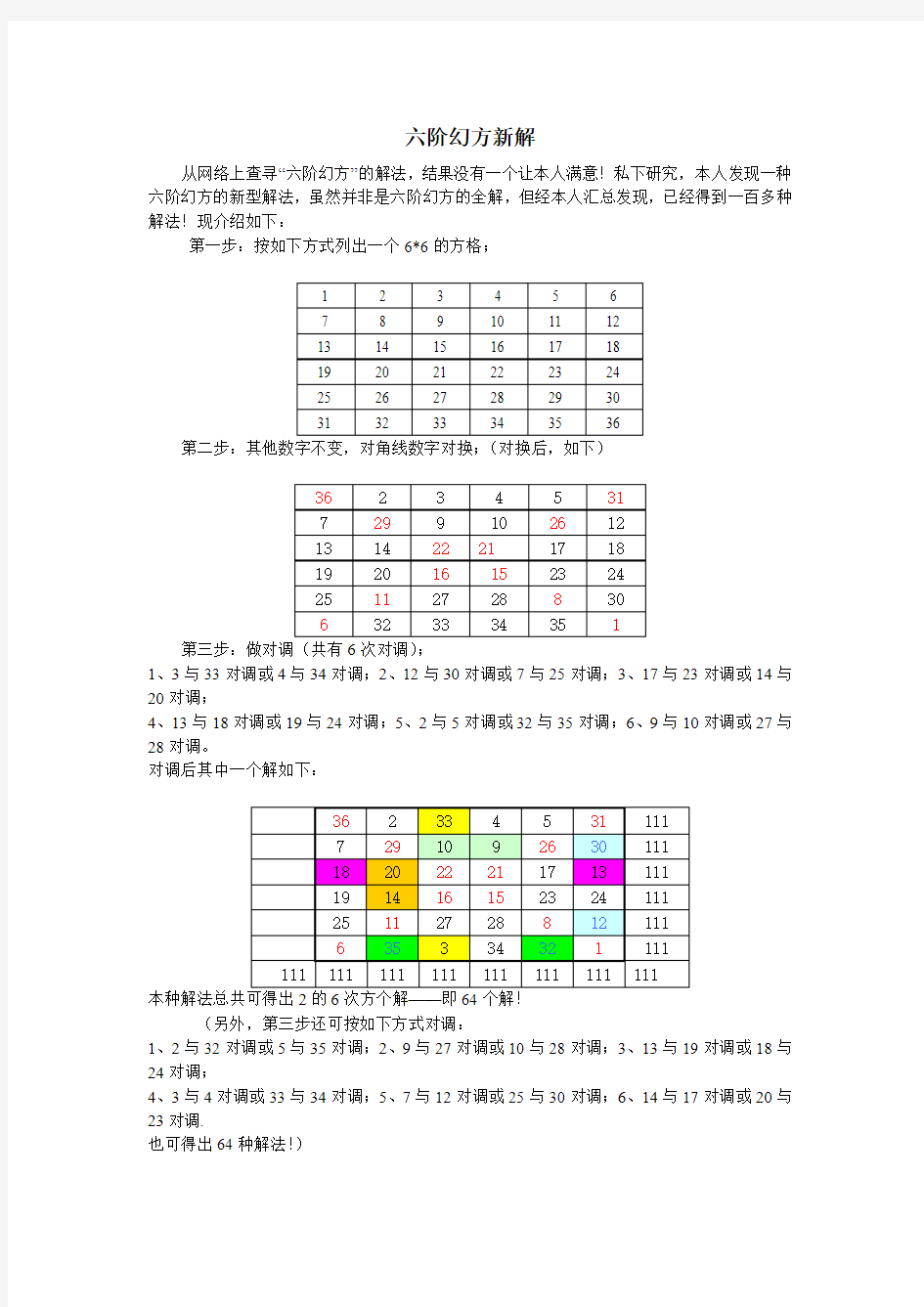
六阶幻方新解
从网络上查寻“六阶幻方”的解法,结果没有一个让本人满意!私下研究,本人发现一种六阶幻方的新型解法,虽然并非是六阶幻方的全解,但经本人汇总发现,已经得到一百多种解法!现介绍如下:
第一步:按如下方式列出一个6*6的方格;
1 2 3 4 5 6
7 8 9 10 11 12
13 14 15 16 17 18
19 20 21 22 23 24
25 26 27 28 29 30
31 32 33 34 35 36
第二步:其他数字不变,对角线数字对换;(对换后,如下)
36 2 3 4 5 31
7 29 9 10 26 12
13 14 22 21 17 18
19 20 16 15 23 24
25 11 27 28 8 30
6 32 33 34 35 1
第三步:做对调(共有6次对调);
1、3与33对调或4与34对调;
2、12与30对调或7与25对调;
3、17与23对调或14与20对调;
4、13与18对调或19与24对调;
5、2与5对调或32与35对调;
6、9与10对调或27与28对调。
对调后其中一个解如下:
36 2 33 4 5 31 111
7 29 10 9 26 30 111
18 20 22 21 17 13 111
19 14 16 15 23 24 111
25 11 27 28 8 12 111
6 35 3 34 32 1 111
111 111 111 111 111 111 111 111
本种解法总共可得出2的6次方个解——即64个解!
(另外,第三步还可按如下方式对调:
1、2与32对调或5与35对调;
2、9与27对调或10与28对调;
3、13与19对调或18与24对调;
4、3与4对调或33与34对调;
5、7与12对调或25与30对调;
6、14与17对调或20与23对调.
也可得出64种解法!)
在一个由若干个排列整齐的数组成的正方形中,图中任意一横行、一纵行及对角线的几个数之和都相等,具有这种性质的图表,称为“幻方”。我国古代称为“河图”、“洛书”,又叫“纵横图”。 1、奇数阶幻方——罗伯特法(也有人称之为楼梯法)(如图一:以五阶幻方为例) 奇数阶幻方 n为奇数(n=3,5,7,9,11……) (n=2×k+1,k=1,2,3,4,5……) 奇数阶幻方最经典的填法是罗伯特法(也有人称之为楼梯法)。填写方法是这样: 把1(或最小的数)放在第一行正中;按以下规律排列剩下的n×n-1个数: (1)每一个数放在前一个数的右上一格; (2)如果这个数所要放的格已经超出了顶行那么就把它放在底行,仍然要放在右一列; (3)如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上一行; (4)如果这个数所要放的格已经超出了顶行且超出了最右列,那么就把它放在前一个数的下一行同一列的格内; (5)如果这个数所要放的格已经有数填入,处理方法同(4)。 这种写法总是先向“右上”的方向,象是在爬楼梯。 口诀: 1居首行正中央, 依次右上莫相忘 上出格时往下放, 右出格时往左放. 排重便往自下放, 右上出格一个样 图一 2、单偶数阶幻方 ()1 2 2+ =m n ——分区调换法(如图二:以六阶幻方为例) ①把()1 2 2+ =m n阶的幻方均分成4个同样的小幻方A、B、C、D(如图二) 图二
(注意A 、B 、C 、D 的相对位置不能改变,因为12+m 为奇数,所以A 、B 、C 、D 均为奇数阶幻方) ② 用连续摆数法在A 中填入21a ——构成幻方,同理,在B 中填入()2221a a ——+、在C 中填入()22312a a ——+、在D 中填入()22413a a ——+均构成幻方(2n a =)(如图三) 图三 (因为12+m 为奇数,所以A 、B 、C 、D 均为奇数阶幻方,必然可以用连续摆数法构造幻方) ③ 在A 的中间一行上从左侧的第二列起取m 个方格,在其它行上则从左侧第一列起取m 个方格,把这些方格中的数与D 中相应方格中的数字对调(如图四): 图四 不管是几阶幻方,在A 中取数时都要从中间一行的左侧第二列开始;因为当6=n 时,1=m ,所以本例中只取了一个数) ④ 在A 中从最右一列起在各行中取1-m 个方格,把这些方格中的数与D 中相应方格中的数字对调。(如图五) 图五 3、双偶数阶幻方m n 4=——轴对称法(如图三:以八阶幻方为例) ① 把m n 4=阶的幻方均分成4个同样的小幻方(如图六) 图六
数独解法 七种解法: 前言 数独这个数字解谜游戏,完全不必要用到算术!会用到的只是推理与逻辑。刚开始接触数独时,即使是只须用到唯一解技巧的简易级谜题,就已可让我们焦头烂额了,但是随着我们深陷数独的迷人世界之后,这类简易级的数独谜题必定在短时间内难再使我们获得征服的满足。于是,当我们逐步深入、进阶到更难的游戏后,我们将会需要发展龈?多的解谜技巧。虽然最好的技巧便是我们自己发现的窍门,这样我们很容易??能记住它们,运用自如,不需要别人来耳提面命。但是如果完全不去观摩学习他人发展出来的技巧,而全靠自己摸索,那将是一个非常坚苦的挑战,也不是正确的学习之道!所以让我们一齐来探讨数独的解谜方法吧! 数独的解谜技巧,刚开始发展时,以直观式的唯一解及摒除法为主,对于初入门的玩家来说,这也是一般人较容易理解、接受的方法,对于一般简易级或中级的数独谜题,如果能灵活运用此二法则,通常已游刃有余。 1.唯一解法 当数独谜题中的某一个宫格因为所处的列、行或九宫格已出现过的数字已达8 个,那么这个宫 格所能填入的数字就剩下这个还没出现过的数字了。 <图1> (9, 8)出现唯一解了
<图1>是最明显的唯一解出现时机,请看第8 行,由(1,8) ~(8,8) 都已填入数字了,只剩(9,8)还是空白,此时(9,8)中应填入的数字,当然就是第8 行中还没出现过的数字了!请一个个数字核对一下,哦!是数字8 还没出现过,所以(9,8) 中该填入的数字就是数字 了。8 出现唯一解了2> (8, 9)<图<图2>是另一个明显出现唯一解的情形,请看第8 列,由(8,1) ~(8,8) 都已填入数字了,只剩(8,9)还是空白,此时(8, 9)中应填入的数字,当然就是第8 列中还没出现过的数字中该填入的数字就是9) (8, 还没出现过,所以9 哦!是数字了!请一个个数 字核对一下, 9 了。数字出现唯一解了图3> (7, 5)<<图3>是另一种明显出现唯一解的情形,请看下中九宫格,在这个九宫格中除了(7, 5)还是空白外,其他宫格都已填有数字了,所以(7, 5)中应填入的数字,当然就是下中九宫格中还没出现过的数字了!请一个个数字核对一下,哦!是数字 1 还没出现过,所以(7, 5) 了。中该填入的数字就是数字1
数独解题方法大全 作者:扬子活力论坛泥瓦匠整理:隱讀書生 数独这个数字解谜游戏,完全不必要用到算术!会用到的只是推理与逻辑。解题方法分两大类:直观法和候选数法。 直观法就是不需要任何辅助工具,从接到数独谜题的那一刻起就可以立即开始解题。绝不猜测。数独直观法解题技巧主要有:唯一解法、基础摒除法、区块摒除法、唯余解法、矩形摒除法、单元摒除法,余数测试法。 候选数法就是解数独题目需先建立候选数列表,根据各种条件,逐步安全的清除每个宫格候选数的不可能取值的候选数,从而达到解题的目的。 使用候选数法一般能解比较复杂的数独题目,但是候选数法的使用没用直观法那么直接,需要先建立一个候选数列表的准备过程。所以实际使用时可以先利用直观法进行解题,到无法用直观法解题时再使用候选数方法解题。 候选数法解题的过程就是逐渐排除不合适的候选数的过程,所以在进行候选数删除的时候一定要小心,确定安全的删除不合适的候选数,否则,很多时候只有重新做题了。有了计算机软件的帮助,使得候选数表的维护变得轻松起来。 数独候选数法解题技巧主要有:唯一候选数法、隐性唯一候选数法、区块删减法、数对删减法、隐性数对删减法、
三链数删减法、隐性三链数删减法、矩形顶点删减法、三链列删减法、关键数删减法、关连数删减法。 一、直观法: 1、唯一解法: 当某行已填数字的宫格达到8个,那么该行剩余宫格能填的数字就只剩下那个还没出现过的数字了。成为行唯一解。 当某列已填数字的宫格达到8个,那么该列剩余宫格能填的数字就只剩下那个还没出现过的数字了。成为列唯一解。 当某九宫格已填数字的宫格达到8个,那么该九宫格剩余宫格能填的数字就只剩下那个还没出现过的数字了。成为九宫格唯一解。 下面是例题: A行已经添入8个数字,A行只有数字3没有出现过,所以A9=3,这是行唯一解。
幻方常规解法汇总 没法,组合数学还考幻方构造。这东西不看解法真不会写,虽然没见有啥用,但还是记录下,免得日后再找。按目前填写幻方的方法,是把幻方分成了三类,即奇数阶幻方、双偶阶幻方、单偶阶幻方。下面按这三类幻方,列出最常用解法(考试用,不求强大,只求有效!)。 奇数阶幻方(罗伯法) 奇数阶幻方最经典的填法是罗伯法。填写的方法是: 把1(或最小的数)放在第一行正中;按以下规律排列剩下的(n×n-1)个数: 1、每一个数放在前一个数的右上一格; 2、如果这个数所要放的格已经超出了顶行那么就把它放在底行,仍然要放在右一列; 3、如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上一行; 4、如果这个数所要放的格已经超出了顶行且超出了最右列,那么就把它放在前一个数的下一行同一列的格内; 5、如果这个数所要放的格已经有数填入,那么就把它放在前一个数的下一行同一列的格内。 例,用该填法获得的5阶幻方: 双偶数阶幻方(对称交换法) 所谓双偶阶幻方就是当n可以被4整除时的偶阶幻方,即4K阶幻方。在说解法之前我们先说明一个“互补数”定义:就是在n 阶幻方中,如果两个数的和等于幻方中最大的数与 1 的和(即n×n+1),我们称它们为一对互补数。如在三阶幻方中,每一对和为10 的数,是一对互补数;在四阶幻方中,每一对和为17 的数,是一对互补数。 双偶数阶幻方的对称交换解法: 先看看4阶幻方的填法:将数字从左到右、从上到下按顺序填写: 内外四个角对角上互补的数相易,(方阵分为两个正方形,外大内小,然后把大正方形的四个对角上的数字对换,小正方形四个对角上的数字对换)即(16,11)(7,10)互换即可。 对于n=4k阶幻方,我们先把数字按顺序填写。写好后,按4×4把它划分成k×k个方阵。因为n是4的倍数,一定能用4×4的小方阵分割。然后把每个小方阵的对角线,象制作4阶幻方的方法一样,对角线上的数字换成互补的数字,就构成幻方。 以8阶幻方为例: (1) 先把数字按顺序填。然后,按
任意阶幻方的构造方法 一、幻方分类 n 表示阶数 二、构造方法 以下幻方均指在n n ?(n 行n 列)的方格里,既不重复也不遗漏地填上1——2n 所构成的幻方。 1、奇数阶幻方——连续摆数法(如图一:以五阶幻方为例) ① 把1填在第一行正中; ② 把i a ()i ≤2放在1-i a 的右上一格;如:3、5、7、8、20等。 ③ 如果i a 所要放的格已超出了顶行,那么就把它放在1-i a 的右一列的最下行;如:2、9、18、25。 ④ 如果i a 所要放的格已超出了最右列,那么就把它放在1-i a 的上一行的最左列;如:4、10、17、23。 ⑤ 如果i a 所要放的格已超出了顶行且超出了最右列,那么就把它放在1-i a 的下一行的同一列的格内;如:16。 ⑥ 如果i a 所要放的格已有数填入,那么就把它放在1-i a 的下一行的同一列的格内。如:6、11、21。 图一 2、单偶数阶幻方()122+ =m n ——分区调换法(如图二:以六阶幻方为例) ① 把()122+=m n 阶的幻方均分成4个同样的小幻方A 、B 、C 、D ;如图二(a ); (注意A 、B 、C 、D 的相对位置不能改变,因为12+m 为奇数,所以A 、B 、C 、D 均为奇数阶幻方) ② 用连续摆数法在A 中填入21a ——构成幻方,同理,在B 中填入() 2221a a ——+、在
C 中填入()22312a a ——+、在 D 中填入() 22413a a ——+均构成幻方(2n a =);如图二(b ); (因为12+m 为奇数,所以A 、B 、C 、D 均为奇数阶幻方,必然可以用连续摆数法构造幻方) ③ 在A 的中间一行上从左侧的第二列起取m 个方格,在其它行上则从左侧第一列起取m 个方格,把这些方格中的数与D 中相应方格中的数字对调;如图二(c 、d ), (不管是几阶幻方,在A 中取数时都要从中间一行的左侧第二列开始;因为当6=n 时,1=m ,所以本例中只取了一个数) ④ 在C 中从最右一列起在各行中取1-m 个方格,把这些方格中的数与B 中相应方格中的数字对调。 (因为01=- m ,所以在C 中没有取数) 图二(d )即为所求幻方。 图二(a ) 图二(b ) 图二(c ) 图二(d ) 3、双偶数阶幻方m n 4=——轴对称法(如图三:以八阶幻方为例) ① 把m n 4=阶的幻方均分成4个同样的小幻方;如图三(a ) ② 在左上角的小幻方每行每列中任取一半的方格加上底色(以便于区分),然后以轴对称的形式在其它三个小幻方中标出方格;如图三(b ) (正确理解“每行每列中任取一半的方格”。本例中因为4=m ,所以在每个小幻方的每行每列上均取2个方格) ③ 从左上角的方格开始,按从左到右、从上到下的次序将1——64从小到大依次填入n 阶幻方,遇到有底色的方格跳过,计数,这样填满了没有底色的方格;如图三(c )
n是它的阶数,比如上面的幻方是3阶。n/2*(n*n+1)为幻方的变幻常数。数学上已经证明,对于n>2,n阶幻方都存在。目前填写幻方的方法,是把幻方分成了三类,每类又有各种各样的填写方法。这里对于这三类幻方,仅举出一种方便手工填写的方法。 1、奇数阶幻方 n为奇数(n=3,5,7,9,11……) (n=2*k+1,k=1,2,3,4,5……) 奇数阶幻方最经典的填法是罗伯特法(也有人称之为楼梯法)。填写方法是这样:把1(或最小的数)放在第一行正中;按以下规律排列剩下的n*n-1个数:(1)、每一个数放在前一个数的右上一格;(2)、如果这个数所要放的格已经超出了顶行那么就把它放在底行,仍然要放在右一列;(3)、如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上一行;(4)、如果这个数所要放的格已经超出了顶行且超出了最右列,那么就把它放在前一个数的下一行同一列的格内;(5)、如果这个数所要放的格已经有数填入,处理方法同(4)。这种写法总是先向“右上”的方向,象是在爬楼梯。 2、双偶阶幻方
方阵 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 (2) 每个小方阵对角线上的数字,换成和它互补的数。 单偶阶幻方 n为偶数,且不能被4整除(n=6,10,14,18,22……) (n=4k+2,k=1,2,3,4,5……) 这是三种里面最复杂的幻方。 以n=10为例。这时,k=2 (1) 把方阵分为A,B,C,D四个象限,这样每一个象限肯定是奇数阶。用楼梯法,依次在A象限,D象限,B象限,C象限按奇数阶幻方的填法填数。
我们用的是降阶法,基本的还原过程如下: 1.中心复原 2.棱合并 3.按三阶还原 4.特殊情况校正 四阶魔方与三阶魔方的区别主要有两点,1.中心块的相对位置不是固定的,也就是说,你可能轻易对出四个黄中红中心块的情况,但是如果对成这样后面就不能还原了,你需要自己在前面几步注意做好中心块的相对位置关系,图所示,上黄下白前红后橙左蓝右绿,然后再继续后面的步骤。2.四阶魔方对好中心块,合并好棱边后,就个三阶魔方,但是这个三阶魔方会出现我们三阶入门教程里的那些不可能出现的情况,也就是 a.需要单独翻转一个注意,我这里说的一个棱边就是指已经合并好的两个棱块) b.只需要交换一对棱边或者一对角块,上面第三个图显示时发生的样子(他要单独只翻转黄红一个棱边,然后还得只交换黄红和黄橙一对棱边),这通常被大家称为四阶魔方需要用两个算法处理一下,他就会变成正常的三阶魔方了,然后你就可以用学过的三阶魔方的任何方法来还原四阶 好,下面我们就来讲解四阶魔方的还原方法了。 (第一步)对好第一面的中心块 这一步最简单,你要对成左边这个样子,基本上这一步的指导方针就是,先对好一对,再对好把两对儿拼起来。请看下面的例子:魔方小站
播放 动画,你也可以 最左边的回到初始状 ,然后用播放条右边 的 和一步一步看。TL'F TU TL' 先对好一对儿黄色小块 右侧的黄色小块要转到前面来 会到 A 位置,为了要两个黄 色小块对成一对,要把前面 的黄色小块先调整到 A 旁 边。 对上第二对儿。对好黄色面上面这个例子大家关键就是学会第二步,看准了右面这个小黄块要到前面的 A 位置来,你就旋转一下前面把另 备到他旁边就对了。这个例子里小黄块是从右边转到前面去还好看一点儿,你也可能碰到小黄块要从后面转到前面,大家就得仔细点,别看错了位置就拼不上了。 有时拼一对儿的时候你要注意一下不要影响了已经对好的另一对儿,如果影响了,就让他们让开,空出一个轨道由旋转了。 以用鼠标拖拽3D动画里 个魔方,以看到魔方背面 的变化。B TU F TD2 超简单吧,这步大家就学会啦。
如何填幻方 幻方最早记载于我国公元前500年的春秋时期《大戴礼》中,这说明我国人民早在2500年前就已经知道了幻方的排列规律。而在国外,公元130年,希腊人塞翁才第一次提起幻方。我国不仅拥用幻方的发明权,而且是对幻方进行深入研究的国家。公元13世纪的数学家杨辉已经编制出3-10阶幻方,记载在他1275年写的《续古摘厅算法》一书中。在欧洲,直到574年,德国著名画家丢功才绘制出了完整的4阶幻方。 数学上已经证明,对于n>2,n阶幻方都存在。目前填写幻方的方法,是把幻方分成了三类,每类又有各种各样的填写方法。 1、奇数阶幻方 n为奇数(n=3,5,7,9,11……) (n=2×k+1,k=1,2,3,4,5……) 奇数阶幻方最经典的填法是罗伯特法(也有人称之为楼梯法)。填写方法是这样: 把1(或最小的数)放在第一行正中;按以下规律排列剩下的n×n-1个数: (1)每一个数放在前一个数的右上一格; (2)如果这个数所要放的格已经超出了顶行那么就把它放在底行,仍然要放在右一列; (3)如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上一行; (4)如果这个数所要放的格已经超出了顶行且超出了最右列,那么就把它放在前一个数的下一行同一列的格内; (5)如果这个数所要放的格已经有数填入,处理方法同(4)。 这种写法总是先向“右上”的方向,象是在爬楼梯。 2、双偶阶幻方 n为偶数,且能被4整除(n=4,8,12,16,20……) (n=4k,k=1,2,3,4,5……) 先说明一个定义。互补:如果两个数字的和,等于幻方最大数和最小数的和,即n*n+1,称为互补。 先看看4阶幻方的填法:将数字从左到右、从上到下按顺序填写: 这个方阵的对角线,已经用颜色标出。将对角线上的数字,换成与它互补(同色)的数字。这里,n×n+1 = 4×4+1 = 17;把1换成17-1 = 16;把6换成17-6 = 11;把11换成17-11 = 6……换完后就是一个四阶幻方。 也可以保留对角线上的数字不动,而将其它的数换为与它互补的数。 对于n=4k阶幻方,我们先把数字按顺序填写。写好后,按4*4把它划分成k2个方阵。因为n是4的倍数,一定能用4*4的小方阵分割。然后把每个小方阵的对角线,象制作4阶幻方的方法一样,对角线上的数字换成互补的数字,就构成幻方。 1 63 6 2 4 5 59 58 8 56 10 11 53 52 14 15 49 48 18 19 45 44 22 23 41 25 39 38 28 29 35 34 32 33 31 30 36 37 27 26 40 24 42 43 21 20 46 47 17 16 50 51 13 12 54 55 9 57 7 6 60 61 3 2 64
六阶魔方 概述 还原六阶魔方首先要做的"还原中心",和我们解法四阶,五阶,七阶的思路是一样的。 解法 完成中心面 剩下最后两面时, 例如图1情况,相信初学者看到这里已经愣住了。这里不能用以前的方法,要用特定的方法。在这里要一个一个完成。 首先确定U面是什么颜色,例如图2是蓝色就要把F面的蓝色中心块都一个一个换到U面,先完成中间2X2的中心块。在这里先将F面和U面的中心块编号一下(图3) (U面和F面的编号一样),所以要把F面的蓝色中心块换到U面。
1.完成2X2的中心块 1、先转F会将F面的蓝色中心块转到7。再转U把U面的黄色中心块转到7 (如果原本就在7就不用转) (图4) 使用公式一 ,变成图 5样子。 图1图2 图3 图4 公式一:3R U 3L’ U’3R’U3L U’ 90度90度90度90度 90度90度90度90度 公式说明: 大写字母前加数字代表第几层;小写字母前加数字表示几层一起转动;字母后加2表示转180°;字母后加“ ' ”表示逆时针。 例如,2R表示右边数第二层顺时转,2r表示右边两层顺时转; 2F表示前面向里第二层顺时转,2f表示前面两层顺时转;
2-3F表示前面向里第二层、第三层同时顺时针转动; 4R和4L表示同一层;4F和4B表示同一层。 2、再将F面的蓝色中心块转到7 ,U面的黄色中心块转到7(图6),重复一次公式一,中间2X2的中心块就完成了。(图7) 图 5 图 6图7图8 2.完成F、U面中心角块 完成F面和U面上中心四个角上的块。即将1.4.13.16完成(图8),红色圈的块。 先转F将F面的蓝色中心块转到4,再转U把U面的黄色中心块转到4 (如果原本就在4就不用转),转一次公式二,会变成图9. 公式二:2R U 2L’U’2R’U 2L U’ 90度90度90度90度
说到幻方和九宫数大多数人都不陌生,在金庸先生著名的武侠小说《射雕英雄传》中就有郭靖在黄蓉的指导下为英姑指点九宫数的排列:“戴九履一,左三右七,二四为肩,六八为足,五居中央。”想必各位朋友也都玩过这个数字游戏,但对幻方又了解多少呢? 500){this.resized=true;this.style.width=500;}" border=0> 幻方又称为纵横图、魔方、魔阵或奇平方,它最早起源于我国。宋代数学家杨辉称之为纵横图。 所谓纵横图,它是由1到n2,这n2个自然数按照一种的规律排列成N行、N列的一个方阵。它具有一种奇妙的性质,在各种几何形状的表上排列适当的数字,如果对这些数字进行简单的逻辑运算时,不论采取哪一条路线,最后得到的和或积都是完全相同的。 关于幻方的起源,我国有“河图”和“洛书”之说。相传在远古时期,伏羲氏取得天下,把国家治理得井井有条,感动了上天于是黄河中跃出一匹龙马,背上驮着一张图,作为礼物献给他,这就是“河图”,也是最早的幻方。伏羲氏凭借着“河图”而演绎出了八卦。 500){this.resized=true;this.style.width=50 0;}" border=0> 后来大禹治洪水时,洛水中浮出一只大乌龟,它的背上有图有字,人们称之为“洛书”。公元前一世纪,西汉宣帝时的博士戴德在他的政治礼仪著作《大戴礼·明堂篇》中就有“二、九、四、七、五、三、六、一、八”的洛书九宫数记载。“洛书”所画的图中共有黑、白圆圈45个。把这些连在一起的小圆和数目表示出来,得到九个数。这九个数就可以组成一个纵横图,也就是记载最早的3阶幻方。
500){this.resized=true;this.style.width=50 0;}" border=0> 洛书被世界公认为组合数学的鼻祖,它是中华民族对人类的伟大贡献之一。同时,洛书以其高度抽象的内涵,对我国古代政治伦理、数学、天文气象、哲学、医学、宗教等等都产生了重要影响。在远古传说中,对于治国安邦上也具有积极的寓意!包括洛书在内的幻方自古以来在亚、欧、美洲不少国家都被作为驱邪避凶的吉祥物,这种古代地域广泛的图腾应该说是极其少见的。 除此之外,还有4阶、5阶...
幻方的填写技巧 一、N阶幻方的分类: 1、奇数阶幻方:当时,称为奇数阶幻方。 2、偶数阶幻方: (1)双偶数幻方:当时,称为双偶数数阶幻方。 (2)单偶数幻方:当)时,称为单偶数阶幻方。 二、幻方的填写方法: 1、奇数阶幻方:可按照如下方法操作: Merzirac法,有人也叫楼梯法,我管它叫斜步法,即走X+Y斜步(数字按右上方顺序填入),-Y跳步(如果右上方已有数字或出了对角线,则向下移一格继续填写)。 其实斜步法可以向4个方向依次填写数字,即右上、右下、左上、左下4个方向,每种斜步都可有2种跳步,即左(右)跳步、上(下)跳步。 对于X+Y斜步相应的跳步可以为-X,-Y。【记住,跳步是X+Y斜步的X(或Y)相反方向即可。如右上方向斜步,跳步就为向左(或向下)一步;左下方向斜步,跳步就为向右(或向上)一步;等等等等】 (2)杨辉“阳动阴静”法 南宋杨辉不仅精通数学,而且精通易学,在他1275年所著的《续古摘奇算法》中,就对河图和洛书的数学问题进行了详尽的研究。其中对3阶幻方的排列,找出了一种奇妙的规律:“九子斜排,上下对易,左右相更,四维挺出,戴九履一,左三右七,二四为肩,六八为足”,清代,
2、双偶数阶幻方:可按照如下方法操作: (一)四阶幻方: (1) 对角线上的数字一律不动; (2) 对角线以外的数字关于对角线交点作中心对称对换位置即可。 (3) 完成后的四阶幻方如下:
(1)对角线上的数字一律不动; (2)对角线以外的数字关于对角线交点作中心对称对换位置即可。 (3) 3、 (按奇数阶幻方填法按区域填写)
(二)十阶幻方:
时光如梦,梦里梦外总是有许多憧憬美好,执着这份美好,烟火的生活在平淡中闻到花香,茶香和米香。 静坐时光,把喧嚣关在窗外,悠然恬淡。一缕缕柔风也会温润流年,一轮明月也会涌出丝丝柔情。 岁月静好,与君语;细水长流,与君同;时光如水,与君老。 相伴的时光,简单微笑着,从容平淡着。如若真心,那份灵犀,那份执意,那份默契,让一切俗世纷扰,也过得惬意悠然。 爱就一个懂,一份守,一个眼神就领会了眼眸里的含义,一个怀抱就温暖了整个身心。 光阴无言流淌,岁月无声的叩问着百味世事,彼此相视一笑,你在,我在,阳光还是那么明媚,日子还是那么温馨,你若安好,岁月无恙。 红尘陌上,择一方心灵的净土,种下文字的馨香,于文字中寻一份感悟,让心安暖;于岁月中守一份懂得,感恩生命。 朝霞暮露,四季更迭,花开花谢皆如画,月圆月缺皆如诗。当时光辗转着记忆的年轮,当清风摇曳起祝福的风铃,我在风中优雅的翩跹,回味携手的光阴,淡淡的犹如一朵茉莉花,洁白淡雅,清香宜人。 在素色光阴里,有古韵婉转的琴音入耳,有清幽淡然的花香入鼻,有真情实意的友情入心,有相处不厌的爱入魂,温柔地牵起时光的手,用善待一朵花开的温婉,来守望一生的幸福。人生会在知足中嫣然一笑,花香依旧。 凉风习习,花影阑珊,瓜果飘香,时光是多么轻盈、温柔和生动。 永远是多长,爱意有多浓,一切无足轻重,只想把此刻定格成温暖的笑靥。回味,感恩,彼此执手的岁月,是多么知足和无悔。
幻方(一) 1. 会用罗伯法填奇数阶幻方 2. 了解偶数阶幻方相关知识点 3. 深入学习三阶幻方 一、幻方起源 也叫纵横图,也就是把数字纵横排列成正方形,因此纵横图又叫幻方.幻方起源于我国,古人还为它编撰了一些神话.传说在大禹治水的年代,陕西的洛水经常大肆泛滥,无论怎样祭祀河神都无济于事,每年人们摆好祭品之后,河中都会爬出一只大乌龟,乌龟壳有九大块,横着数是3行,竖着数是3列,每块乌龟壳上都有几个点点,正好凑成1至9的数字,可是谁也弄不清这些小点点是什么意思.一次,大乌龟又从河里爬上来,一个看热闹的小孩惊叫起来:“瞧多有趣啊,这些点点不论横着加、竖着加还是斜着加,结果都等于十五!”于是人们赶紧把十五份祭品献给河神,说来也怪,河水果然从此不再泛滥了.这个神奇的图案叫做“幻方”,由于它有3行3列,所以叫做“三阶幻方”,这个相等的和叫做“幻和”.“洛书”就是幻和为15的三阶幻方.如下图: 98 76 54321 我国北周时期的数学家甄鸾在《算数记遗》里有一段注解:“九宫者,二四为肩,六八为足,左三右七,戴九履一,五居中央.”这段文字说明了九个数字的排列情况,可见幻方在我国历史悠久.三阶幻方又叫做九宫图,九宫图的幻方民间歌谣是这样的:“四海三山八仙洞,九龙五子一枝连;二七六郎赏月半,周围十五月团圆.”幻方的种类还很多,这节课我们将学习认识了解它们. 二、幻方定义 幻方是指横行、竖列、对角线上数的和都相等的数的方阵,具有这一性质的33?的数阵称作三阶幻方,44?的数阵称作四阶幻方,55?的称作五阶幻方……如图为三阶幻方、四阶幻方的标准式样, 9 87654 32 1 13 414151 6 1297 8 105113 2 16 三、解决这幻方常用的方法 ⑴适用于所有奇数阶幻方的填法有罗伯法.口诀是:一居上行正中央,后数依次右上连.上出框时往下填,右出框时往左填.排重便在下格填,右上排重一个样. ⑵适用于三阶幻方的三大法则有: ①求幻和: 所有数的和÷行数(或列数) ②求中心数:我们把幻方中对角线交点的数叫“中心数”,中心数=幻和÷3. ③角上的数=与它不同行、不同列、不同对角线的两数和÷2. 四、数独 知识点拨 教学目标
第七节巧填幻方【知识要点】 将九个不同的数填在3×3(三行三列)的方格中,如果满足每个 横行、每个竖列和每条对角线上的三个数之和都相等,那么这样的图 称为“三阶幻方”,这个相等的和称为幻和。 在三阶幻方中有:中间数A=总和÷9=幻和÷3 D=(B+C)÷2 【典型例题】 例1 请你把5,6,7,8,9,10,11,12,13这几个数字填入下面的方格中组成一个三阶幻方。 例2 找出九个连续的自然数,分别填入下图的空格内,构成一个幻和为120的三阶幻方。D B A C
例3 在下面空格中填入七个自然数,使得每行、每列及每条对角线上的三个数之和是60。 14 28 例4 在下图中的空格内填入不大于15且互不相同的自然数,使每一个横行、每一竖列及每条对角线上的三个数之和都等于30。 8
随堂小测 1.将2,4,6,8,10,12,14,16,18这九个数分别填入下面图中的方格内,使每行、每列和每条对角线上的和都相等。 2.用3~27这25个数排成一个五阶幻方。 3.请编出一个三阶幻方,使其幻和为24。
4.请在下面的空格中填上适当的数,使其成为一个幻 和为27的幻方。 5.在下图的空格中填入不大于15且互不相同的自然数, 使其成为幻和为30的幻方。 6.你能在下面3×3的方格表中每个格子里都填一个自然数,使得每行、每列及每条对角线上的三数之和都等于1997吗?若能,请举出一个例,若不能请说明理由。 5 6 14
课后作业 1.请自编一个幻和为90的三阶幻方。 2.补充下面的幻方,使其幻和为33。 3.将图中的数重新排列,使得横行、竖行、对角线上的三个数的和都相等。7 12 22 30 38 22 30 38 22 30 38
创作编号: GB8878185555334563BT9125XW 创作者:凤呜大王* 四阶幻方是最简单的双偶幻方,其构成方法就是两句话: 【顺序填数;以中心点对称互换数字】.以1-16构成的四阶幻方为例: 1、先把1放在四阶幻方4个角的任意一个角格,按同一个方向按顺序依次填 写其余数. 如图:按行从左向右顺序排数. 2、以中心点对称互换数字.(有两种对称交换的方法) 1)、以中心点对称交换对角线上的数(即1-16、4-13、6-11、7-10互换),完成幻方,幻和值=34. 2)、以中心点对称交换非对角线上的数(即2-15、3-14、5-12、8-9互换),完成幻方,幻和值=34. 什么样的16个数能构成四阶幻方呢?【4个数一组的4组数(共16个数), 组与组对称等差,每组数与数对称等差,这样的16个数能构成四阶幻方(其中就包括等差的16个数).】
如图 上图,每组数与数以2-3-2对称等差,组与组以10-20-10对称等差. 下图,每组数与数以1-2-1对称等差,组与组以10-20-10对称等差. 再如:
上图,每组数与数等差为1,组与组等差为5. 中图,每组数与数等差为1,组与组以5-10-5对称等差. 下图,每组数与数以2-3-2对称等差,组与组以5-10-5对称等差. 【四阶幻方的特点:】 1、互换对称的行(列),幻方成立. 2、互换一侧的行(或列),再互换另一侧的行(或列),幻方亦成立. 3、互换不对称的行(或列),再互换另外不对称的行(或列),幻方亦成立. 4、平移互换对角的行或列、平移互换对角,幻方成立. 另,每16个能构成四阶幻方的数,幻方的填法有880种.
四阶魔方: 交换两个对面棱块:MR2 U2 MR2 U2 MU2 MR2 MU2 翻正一个棱块组: MR2 B2 U2 ML U2 MR' U2 MR U2 F2 MR F2 ML' B2 MR2 五阶魔方: 1. 还原中心 2. 还原棱块 3. 按三阶魔方还原 第一步:还原中心(其实只要自己转转魔方,就会转好,但对初学者来说也有二种特殊情况)我们要记住两个公式: 公式一:TR' F' MR' F TR F' MR 公式二:TR U TR' U TR U2 TR' 公式部分说明: F':表示前面的一层逆时针转90度; MR :右边向内的第三层也就是中间层逆时针转90度; TR:表示右边向内的两层同时顺时针转90度; MR:右边向内的第三层也就是中间层顺时针转90度; 其它可类推,或参见[魔方公式中的各种符号说明]? 这两个公式处理的情况如下图: 公式一是处理第一种情况,公式二是处理第二种情况? 第二步:还原棱块 大家记四个公式吧,在四阶魔方的还原里,我们已经用过的,四阶的棱块还原,完全适用于五阶公式三:TR2 B2 U2 TL U2 TR' U2 TR U2 F2 TR F2 TL' B2 TR2 公式四:TL' U2 TL' U2 F2 TL' F2 TR U2 TR' U2 TL2
公式五:MU' R U R' F R' F' R MU 公式六:TR2 B2 TR' U2 TR' U2 B2 TR' B2 TR B2 TR' B2 TR2 这四个公式分别对应下面四种情况: 翻正一边的中块:TR2 B2 U2 TL U2 TR' U2 TR U2 F2 TR F2 TL' B2 TR2 交换对边侧块:TL' U2 TL' U2 F2 TL' F2 TR U2 TR' U2 TL2 同时翻正对边中块:MU' R U R' F R' F' R MU 交换对边中块:TR2 B2 TR' U2 TR' U2 B2 TR' B2 TR B2 TR' B2 TR2 六阶魔方 6x6魔术方块教学 首先要完成中心的第一面(相信大家只要理解一下就会了)
数独的直观式解题技巧 直观法概说 前言 数独这个数字解谜游戏,完全不必要用到算术!会用到的只是推理与逻辑。刚开始接触数独时,即使是只须用到"基础摒除法"及"唯一解法"技巧的简易级谜题,就已可让我们焦头烂额了,但是随着我们深陷数独的迷人世界之后,这类简易级的数独谜题必定在短时间内难再使我们获得征服的满足。于是,当我们逐步深入、进阶到更难的游戏后,我们将会需要发展出更多的解谜技巧。虽然最好的技巧便是我们自己发现的窍门,这样我们很容易就能记住它们,运用自如,不需要别人来耳提面命。但是如果完全不去观摩学习他人发展出来的技巧,而全靠自己摸索,那将是一个非常坚苦的挑战,也不是正确的学习之道!所以让我们一齐来探讨数独的解谜方法吧! 数独的解谜技巧,刚开始发展时,以直观法为主,对于初入门的玩家来说,这也是一般人较容易理解、接受的方法,对于一般报章杂志及大众化网站上的数独谜题而言,如果能灵活直观法的各项法则,通常已游刃有余。 直观法详说 直观法的特性: 1.不需任何辅助工具就可应用。所以要玩报章杂志上的数独谜题时,只要有一枝 笔就可以开始了,有人会说:可能需要橡皮擦吧答案是:不用!只要你把握数 独游戏的填制原则:绝不猜测。灵活运用本站所介绍的直观填制法,确实可以 不必使用橡皮擦。
2.从接到数独谜题的那一刻起就可以立即开始解题。 3.初学者或没有计算机辅助时的首要解题方法。 4.相对而言,能解出的谜题较简单。 直观法的主要的技巧: 1.基础摒除法。 2.唯一解法。 3.区块摒除法。 4.唯余解法。 5.单元摒除法。 6.矩形摒除法。 7.余数测试法。 基础摒除法 前言 对第一次接触数独游戏,接受了 1 ~ 9 的数字在每一行、每一列、每一个九宫格都只能出现一次的规则后,开始要解题的玩家来说,基础摒除法绝对是他第一个想到及使用的方法,十分的自然、也十分的简易。 如果能够细心、系统化的运用基础摒除法,一般报章杂志或较大众化的数独网站上的数独谜题几乎全部可解出来。只不过大部分的玩家都不知如何系统化的运用基础摒除法罢了! 基础摒除法虽然简单,但在实际应用时,仍然可分成三个部分:
巧填奇数阶幻方 月日姓名 【知识要点】 在3×3或4×4……的正方形,每行每列及每条对角线上的和都相等的填有数的数阵图叫做幻方。三阶幻方是最基本的幻方,构造这个幻方可以有很多种方法。我们在这里介绍其中最常用的一种:罗伯法: 法国人罗伯总结出了,到目前为止,构造3价连续自然数幻方的最简单易行的方法:“罗伯法”。这种方法还可以用于构造5阶、7阶……所有奇数阶幻方。 罗伯法的具体方法可以总结口诀如下: “1”坐边中间,斜着把数填。 出边填对面,遇数往下旋。 出角仅一次,转回下格间。 【典型例题】 例1:用1~9这九个数编排一个三阶幻方。使每行每列及对角上的数之和是15。 练习1:用3~11这九个数补全图中的三阶幻方,并求幻和。 例2:用1~25这25个数补全图1中的五阶幻方,并求幻和 图1 图2 大比拼:用1~49这49个数补全图2中的七阶幻方,并求幻和
例3. 如下图,右方格表中的每个方格中填入一个字母,使得方格表中 每行、每列及每条对角线上的四个方格中的字母都是A 、B 、C 、D (排列顺序不限),那么表中*处应填的字母是什么 作业:从1~100中找出25个连续数填入以下五阶幻方中, 使每一行、每一列及每条对角线上的数的和都相等。 相关习题 1.在下面空格中填入适当的数,使每行、每列及两条对角线上的三个数的和都等于15。 第1题 第2题图 第3题图 2.把3到11这9个数字填入下图中,使每行、每列及每条对角线上三个数的和都相等。 3.把12到 36这25个数填入下图中,使每行、每列及每条对角线上5个数的和都相等。 4.使每行每列对角线上的字母都是ABCD 第4题 第5题 第6题 5.在下图的空格中填入适当的数,使每行、每列两条对角线上的三个数的和都等于18。 6.如图,一个方格表内每行、每列及每对角线上的三个数的和都相等。那么x= 。 7.将图中的数重新排列,使每行、每列及每条对角线上的三个数的和都相等。 8 7 2 A B C C D * 21 23 30 × 24 7 2 5 2 2 2 5 5 5 8 8 8
四阶魔方还原图解+说明
四阶魔方图解还原(转) 个人日记2010-04-08 18:41:53 阅读1399 评论0 字号:大中小订阅 四阶魔方归位3 四阶魔方对好中心块,合并好棱边后,就完全变成了一个三阶魔方,但是这个三阶魔方会出现我们三阶入门教程里的那些不可能出现的情况,也就是 a.需要单独翻转一个棱边的朝向(注意,我这里说的一个棱边就是指已经合并好的两个棱块) b.只需要交换一对棱边或者一对角块,上面第三个图显示了a,b情况同时发生的样子(他要单独只翻转黄红一个棱边,然后还得只交换黄红和黄橙一对棱边),这通常被大家称为四阶魔方的特殊情况,需要用两个算法处理一下,他就会变成正常的三阶魔方了,然后你就可以用学过的三阶魔方的任何方法来还原四阶魔方了。好,下面我们就来讲解四阶魔方的还原方法了。 在开始之前,我想请大家注意,有的朋友向我反映看这个教程之后觉得只看到了一些例子,而自己手中的魔方还是不会拧,这样的朋友就是缺少自己实践的过程。四阶魔方其实就是对中心块的部分比较难讲解,也比较需要一点理解,弄懂了这部分,其实四阶魔方就没什么了,所以大家在前面几步我建议以自己为主,教程为辅,自己看到一个思路之后就试着自己把六面的中心块拼好,这样学习会更有效率也更有乐趣。其实基本上就是两个技巧,一个是去、让、回,一个是在不影响其他面的情况下,把两对拼在一起。另外需要注意的一点就是六面颜色相对位置要你自己来对好,掌握了这3点大家就可以大胆实践了。(第一步)对好第一面的中心块 这一步最简单,你要对成左边这个样子,基本上这一步的指导方针就是,先对好一对,再对好一对,再把两对儿拼起来。请看下面的例子:魔方小站
学号 1250901205 学年论文 (2016届本科) 题目:浅谈幻方以及其解法 学院:数学与统计学院 专业:数学与应用数学 作者姓名:甘天明 指导教师:任天胜职称: 副教授 完成日期: 2014 年 12 月 18 日
浅谈幻方以及其解法 甘天明指导教师:任天胜 (河西学院数学与应用数学专业2016届2班05号甘肃张掖 734000) 摘要多少世纪以来,人们对幻方总是怀着浓厚的兴趣,从古代起幻方就跟某些超自然和魔术的领域相联系。在古代亚洲的城市,人们在考古挖掘中发现了它们。有关幻方的最早纪录,是约于公元前2200年在中国出现的“洛书”,传说这个幻方最初是大禹在黄河岸边的一只神龟的背上看到的。 幻方,有时又称魔方(该称呼现一般指立方体的魔术方块)或纵横图,有一组排放在正方形中的整数组成,其每行、每列以及两条对角线上的数之和均相等。幻方起源于我国,并由我国传到全世界,在这漫长的历史中,幻方也得到了广泛的发展和进步。 本文主要分为两部分,第一部分从幻方的历史和发展,幻方问题的研究以及幻方的应用来认识幻方;第二部分主要介绍幻方的解法。 关键字: 幻方;幻和;奇幻方;偶幻方. 1 引言 我国的纵横图通过东南亚国家,印度和阿拉伯传到西方。由于纵横图具有十分奇幻的特性,西方把纵横图叫做 Magic Square,翻译成中文就是“幻方”或“魔方”。在一个由若干个排列整齐的数组成的正方形中,图中任意一横行、一纵列及对角线的几个数之和都相等,具有这种性质的图表,称为“幻方”。 幻方问题是具有悠久历史的复杂排列组合问题。幻方问题的复杂性不仅在于解的多样性随阶数指数递增,而且在于解在可行排列空间中所占的比例随阶数指数递减。 此外,在文章中,简单介绍了幻方在数学、智力开发、科学以及艺术中的应用,我们从多个角度去探寻幻方的历史,发展和在现实生活中的应用,以此来进一步加深对幻方的理解。 在文章第二部分,也介绍了幻方的几种解法,从不同的角度对幻方的解法做了一点讨论与研究。 2预备知识 的方阵中,放入从1开始的2n个定义2.1 幻方,也叫纵横图,就是在n n 自然数,在一定的布局下,其各行、各列和两条对角线上的数字之和正好相等。 定义2.2 幻方的各行、各列和两条对角线上的数字之和相等的和数即为幻和,也叫幻方常数。 定义2.3 奇阶幻方:当幻方中的n为奇数时,我们称幻方为奇阶幻方。
n阶幻方的填法 Revised by Petrel at 2021
n阶幻方的填法(n≥3)幻方,亦称纵横图。台湾称为魔术方阵。将自然数1,2,3,……n2排列成一个n2方阵,使得每行、每列以及两对角线上的各个数之和都相等,等于这样的方阵称为幻方。 幻方最早记载于我国公元前500年的春秋时期《大戴礼》中,这说明我国人民早在2500年前就已经知道了幻方的排列规律。而在国外,公元130年,希腊人塞翁才第一次提起幻方。我国不仅拥用幻方的发明权,而且是对幻方进行深入研究的国家。公元13世纪的数学家杨辉已经编制出3-10阶幻方,记载在他1275年写的《续古摘厅算法》一书中。在欧洲,直到574年,德国着名画家丢功才绘制出了完整的4阶幻方。例如:把1,2,3,4,5,6,7,8,9填入3*3的格子,使得:每行、每列、两条对角线的和是15。 816 357 492 n是它的阶数,比如上面的幻方是3阶。n/2*(n*n+1)为幻方的变幻常数。数学上已经证明,对于n>2,n阶幻方都存在。目前填写幻方的方法,是把幻方分成了三类,每类又有各种各样的填写方法。这里对于这三类幻方,仅举出一种方便手工填写的方法。 1、奇数阶幻方 n为奇数(n=3,5,7,9,11……)(n=2*k+1,k=1,2,3,4,5……)奇数阶幻方最经典的填法是罗伯特法(也有人称之为楼梯方)。填写方法是这样:把1(或最
小的数)放在第一行正中;按以下规律排列剩下的n*n-1个数:(1)、每一个数放在前一个数的右上一格;(2)、如果这个数所要放的格已经超出了顶行那么就把它放在底行,仍然要放在右一列;(3)、如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上一行;(4)、如果这个数所要放的格已经超出了顶行且超出了最右列,那么就把它放在前一个数的下一行同一列的格内;(5)、如果这个数所要放的格已经有数填入,处理方法同(4)。这种写法总是先向“右上”的方向,象是在爬楼梯。 2、双偶阶幻方 n为偶数,且能被4整除(n=4,8,12,16,20……)(n=4k,k=1,2,3,4,5……)先说明一个定义: 互补:如果两个数字的和,等于幻方最大数和最小数的和,即n*n+1,称为互补。 先看看4阶幻方的填法:将数字从左到右、从上到下按顺序填写: 这个方阵的对角线,已经用蓝色标出。将对角线上的数字,换成与它互补的数字。这里,n*n+1=4*4+1=17;把1换成17-1=16;把6换成17-6=11;把11换成17-11=6……换完后就是一个四阶幻方。