
一、二次函数 真题与模拟题分类汇编(难题易错题)
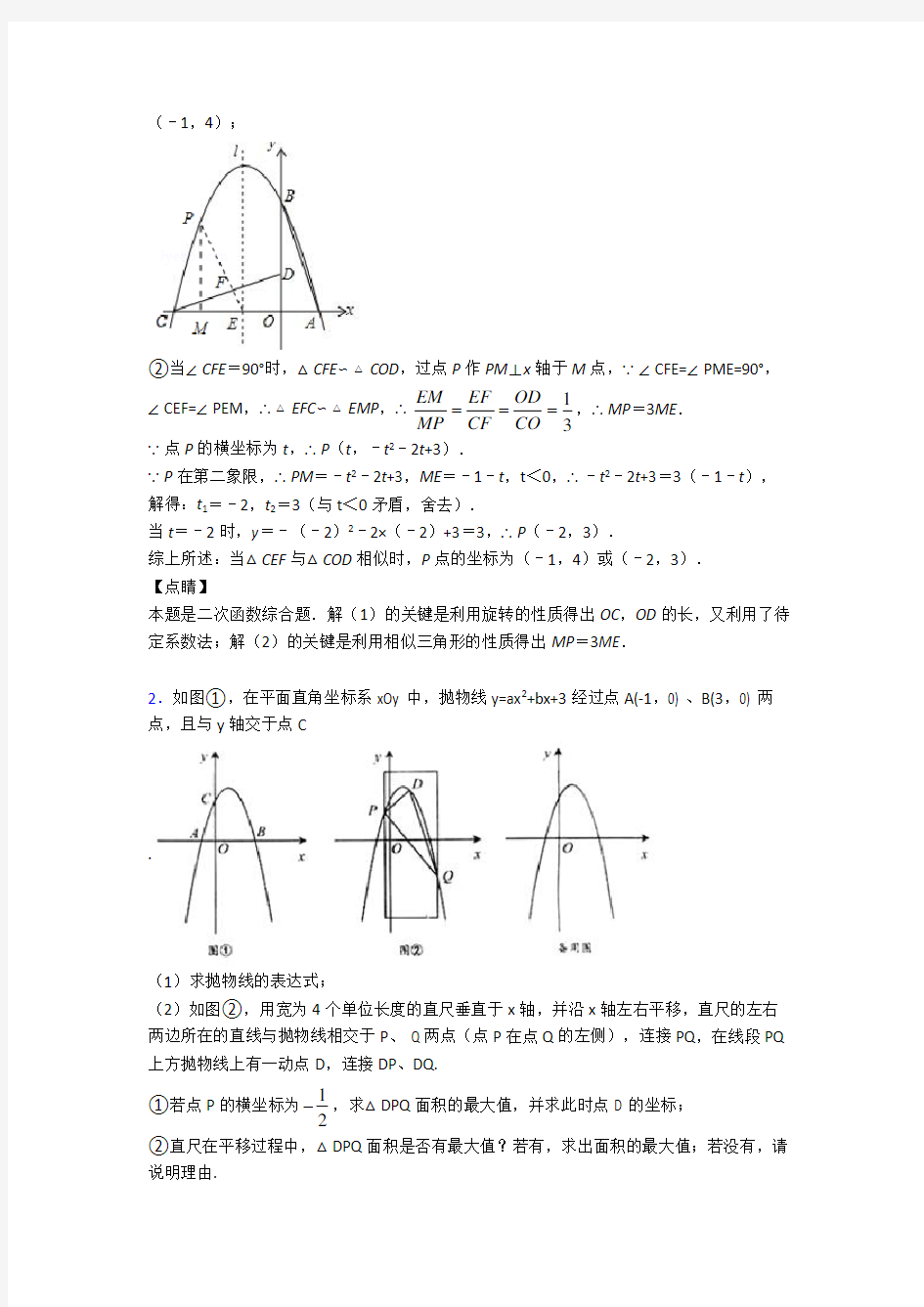
1.如图,在平面直角坐标系中有一直角三角形AOB ,O 为坐标原点,OA =1,tan ∠BAO =3,将此三角形绕原点O 逆时针旋转90°,得到△DOC ,抛物线y =ax 2+bx +c 经过点A 、B 、C .
(1)求抛物线的解析式;
(2)若点P 是第二象限内抛物线上的动点,其横坐标为t ,设抛物线对称轴l 与x 轴交于一点E ,连接PE ,交CD 于F ,求以C 、E 、F 为顶点三角形与△COD 相似时点P 的坐标. 【答案】(1)抛物线的解析式为y=﹣x 2﹣2x+3;(2)当△CEF 与△COD 相似时,P 点的坐标为(﹣1,4)或(﹣2,3). 【解析】 【分析】
(1)根据正切函数,可得OB ,根据旋转的性质,可得△DOC ≌△AOB ,根据待定系数法,可得函数解析式;
(2)分两种情况讨论:①当∠CEF =90°时,△CEF ∽△COD ,此时点P 在对称轴上,即点P 为抛物线的顶点;②当∠CFE =90°时,△CFE ∽△COD ,过点P 作PM ⊥x 轴于M 点,得到△EFC ∽△EMP ,根据相似三角形的性质,可得PM 与ME 的关系,解方程,可得t 的值,根据自变量与函数值的对应关系,可得答案. 【详解】
(1)在Rt △AOB 中,OA =1,tan ∠BAO OB
OA
=
=3,∴OB =3OA =3. ∵△DOC 是由△AOB 绕点O 逆时针旋转90°而得到的,∴△DOC ≌△AOB ,∴OC =OB =3,OD =OA =1,∴A ,B ,C 的坐标分别为(1,0),(0,3),(﹣3,0),代入解析式为
09303a b c a b c c ++=??-+=??=?
,解得:123a b c =-??
=-??=?,抛物线的解析式为y =﹣x 2﹣2x +3;
(2)∵抛物线的解析式为y =﹣x 2﹣2x +3,∴对称轴为l 2b
a
=-=-1,∴E 点坐标为(﹣1,0),如图,分两种情况讨论:
①当∠CEF =90°时,△CEF ∽△COD ,此时点P 在对称轴上,即点P 为抛物线的顶点,P
(﹣1,4);
②当∠CFE =90°时,△CFE ∽△COD ,过点P 作PM ⊥x 轴于M 点,∵∠CFE=∠PME=90°,
∠CEF=∠PEM ,∴△EFC ∽△EMP ,∴
1
3
EM EF OD MP CF CO ===,∴MP =3ME . ∵点P 的横坐标为t ,∴P (t ,﹣t 2﹣2t +3).
∵P 在第二象限,∴PM =﹣t 2﹣2t +3,ME =﹣1﹣t ,t <0,∴﹣t 2﹣2t +3=3(﹣1﹣t ),解得:t 1=﹣2,t 2=3(与t <0矛盾,舍去).
当t =﹣2时,y =﹣(﹣2)2﹣2×(﹣2)+3=3,∴P (﹣2,3).
综上所述:当△CEF 与△COD 相似时,P 点的坐标为(﹣1,4)或(﹣2,3). 【点睛】
本题是二次函数综合题.解(1)的关键是利用旋转的性质得出OC ,OD 的长,又利用了待定系数法;解(2)的关键是利用相似三角形的性质得出MP =3ME .
2.如图①,在平面直角坐标系xOy 中,抛物线y=ax 2+bx+3经过点A(-1,0) 、B(3,0) 两点,且与y 轴交于点C
.
(1)求抛物线的表达式;
(2)如图②,用宽为4个单位长度的直尺垂直于x 轴,并沿x 轴左右平移,直尺的左右两边所在的直线与抛物线相交于P 、 Q 两点(点P 在点Q 的左侧),连接PQ ,在线段PQ 上方抛物线上有一动点D ,连接DP 、DQ. ①若点P 的横坐标为1
2
-
,求△DPQ 面积的最大值,并求此时点D 的坐标; ②直尺在平移过程中,△DPQ 面积是否有最大值?若有,求出面积的最大值;若没有,请说明理由.
【答案】(1)抛物线y=-x 2+2x+3;(2)①点D ( 31524
,);②△PQD 面积的最大值为8 【解析】
分析:(1)根据点A 、B 的坐标,利用待定系数法即可求出抛物线的表达式;
(2)(I )由点P 的横坐标可得出点P 、Q 的坐标,利用待定系数法可求出直线PQ 的表达式,过点D 作DE ∥y 轴交直线PQ 于点E ,设点D 的坐标为(x ,-x 2+2x+3),则点E 的坐标为(x ,-x+5
4
),进而即可得出DE 的长度,利用三角形的面积公式可得出S △DPQ =-2x 2+6x+
7
2
,再利用二次函数的性质即可解决最值问题; (II )假设存在,设点P 的横坐标为t ,则点Q 的横坐标为4+t ,进而可得出点P 、Q 的坐标,利用待定系数法可求出直线PQ 的表达式,设点D 的坐标为(x ,-x 2+2x+3),则点E 的坐标为(x ,-2(t+1)x+t 2+4t+3),进而即可得出DE 的长度,利用三角形的面积公式可得出S △DPQ =-2x 2+4(t+2)x-2t 2-8t ,再利用二次函数的性质即可解决最值问题. 详解:(1)将A (-1,0)、B (3,0)代入y=ax 2+bx+3,得:
309330a b a b -+??
++?==,解得:1
2a b -???
==, ∴抛物线的表达式为y=-x 2+2x+3. (2)(I )当点P 的横坐标为-12
时,点Q 的横坐标为7
2,
∴此时点P 的坐标为(-
12,74
),点Q 的坐标为(72,-9
4).
设直线PQ 的表达式为y=mx+n , 将P (-
12,74
)、Q (72,-9
4)代入y=mx+n ,得:
1
724
792
4m n m n ?-+????+-??==,解得:154m n -?????==,
∴直线PQ 的表达式为y=-x+
5
4
. 如图②,过点D 作DE ∥y 轴交直线PQ 于点E ,
设点D的坐标为(x,-x2+2x+3),则点E的坐标为(x,-x+5
4
),
∴DE=-x2+2x+3-(-x+5
4)=-x2+3x+
7
4
,
∴S△DPQ=1
2
DE?(x Q-x P)=-2x2+6x+
7
2
=-2(x-
3
2
)2+8.
∵-2<0,
∴当x=3
2时,△DPQ的面积取最大值,最大值为8,此时点D的坐标为(
3
2
,
15
4
).
(II)假设存在,设点P的横坐标为t,则点Q的横坐标为4+t,
∴点P的坐标为(t,-t2+2t+3),点Q的坐标为(4+t,-(4+t)2+2(4+t)+3),利用待定系数法易知,直线PQ的表达式为y=-2(t+1)x+t2+4t+3.
设点D的坐标为(x,-x2+2x+3),则点E的坐标为(x,-2(t+1)x+t2+4t+3),∴DE=-x2+2x+3-[-2(t+1)x+t2+4t+3]=-x2+2(t+2)x-t2-4t,
∴S△DPQ=1
2
DE?(x Q-x P)=-2x2+4(t+2)x-2t2-8t=-2[x-(t+2)]2+8.
∵-2<0,
∴当x=t+2时,△DPQ的面积取最大值,最大值为8.
∴假设成立,即直尺在平移过程中,△DPQ面积有最大值,面积的最大值为8.
点睛:本题考查了待定系数法求二次(一次)函数解析式、二次(一次)函数图象上点的坐标特征、三角形的面积以及二次函数的最值,解题的关键是:(1)根据点的坐标,利用待定系数法求出二次函数表达式;(2)(I)利用三角形的面积公式找出S△DPQ=-
2x2+6x+7
2
;(II)利用三角形的面积公式找出S△DPQ=-2x2+4(t+2)x-2t2-8t.
3.对于某一函数给出如下定义:若存在实数m,当其自变量的值为m时,其函数值等于﹣m,则称﹣m为这个函数的反向值.在函数存在反向值时,该函数的最大反向值与最小反向值之差n称为这个函数的反向距离.特别地,当函数只有一个反向值时,其反向距离n为零.
例如,图中的函数有4,﹣1两个反向值,其反向距离n等于5.
(1)分别判断函数y=﹣x+1,y=
1
x
-,y=x2有没有反向值?如果有,直接写出其反向距
离;
(2)对于函数y=x2﹣b2x,
①若其反向距离为零,求b的值;
②若﹣1≤b≤3,求其反向距离n的取值范围;
(3)若函数y=
2
2
3()
3()
x x x m
x x x m
?-≥
?
--<
?
请直接写出这个函数的反向距离的所有可能值,并写出
相应m的取值范围.
【答案】(1)y=?1
x
有反向值,反向距离为2;y=x2有反向值,反向距离是1;(2)
①b=±1;②0≤n≤8;(3)当m>2或m≤﹣2时,n=2,当﹣2<m≤2时,n=4.
【解析】
【分析】
(1)根据题目中的新定义可以分别计算出各个函数是否有方向值,有反向值的可以求出相应的反向距离;
(2)①根据题意可以求得相应的b的值;
②根据题意和b的取值范围可以求得相应的n的取值范围;
(3)根据题目中的函数解析式和题意可以解答本题.
【详解】
(1)由题意可得,
当﹣m=﹣m+1时,该方程无解,故函数y=﹣x+1没有反向值,
当﹣m=
1
m
-时,m=±1,∴n=1﹣(﹣1)=2,故y=
1
x
-有反向值,反向距离为2,
当﹣m=m2,得m=0或m=﹣1,∴n=0﹣(﹣1)=1,故y=x2有反向值,反向距离是1;
(2)①令﹣m=m2﹣b2m,
解得,m=0或m=b2﹣1,
∵反向距离为零,
∴|b2﹣1﹣0|=0,
解得,b=±1;
②令﹣m=m2﹣b2m,
解得,m=0或m=b2﹣1,
∴n=|b2﹣1﹣0|=|b2﹣1|,
∵﹣1≤b≤3,∴0≤n≤8;
(3)∵y=
2
2
3()
3() x x x m
x x x m
?-≥
?
--<
?
,
∴当x≥m时,
﹣m=m2﹣3m,得m=0或m=2,
∴n=2﹣0=2,
∴m>2或m≤﹣2;
当x<m时,
﹣m=﹣m2﹣3m,
解得,m=0或m=﹣4,
∴n=0﹣(﹣4)=4,
∴﹣2<m≤2,
由上可得,当m>2或m≤﹣2时,n=2,
当﹣2<m≤2时,n=4.
【点睛】
本题是一道二次函数综合题,解答本题的关键是明确题目中的新定义,找出所求问题需要的条件,利用新定义解答相关问题.
4.如图,抛物线y=﹣x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接DB.
(1)求此抛物线的解析式及顶点D的坐标;
(2)点M是抛物线上的动点,设点M的横坐标为m.
①当∠MBA=∠BDE时,求点M的坐标;
②过点M作MN∥x轴,与抛物线交于点N,P为x轴上一点,连接PM,PN,将△PMN 沿着MN翻折,得△QMN,若四边形MPNQ恰好为正方形,直接写出m的值.
【答案】(1)(1,4)(2)①点M坐标(﹣1
2
,
7
4
)或(﹣
3
2
,﹣
9
4
);②m的值
317
±117
±【解析】
【分析】
(1)利用待定系数法即可解决问题;
(2)①根据tan∠MBA=
223
3
m m
MG
BG m
-++
=
-
,tan∠BDE=
BE
DE
=
1
2
,由∠MBA=∠BDE,
构建方程即可解决问题;②因为点M、N关于抛物线的对称轴对称,四边形MPNQ是正方形,推出点P是抛物线的对称轴与x轴的交点,即OP=1,易证GM=GP,即|-
m2+2m+3|=|1-m|,解方程即可解决问题.
【详解】
(1)把点B(3,0),C(0,3)代入y=﹣x2+bx+c,
得到
930
{
3
b c
c
-++=
=
,解得
2
{
3
b
c
=
=
,
∴抛物线的解析式为y=﹣x2+2x+3,
∵y=﹣x2+2x﹣1+1+3=﹣(x﹣1)2+4,
∴顶点D坐标(1,4);
(2)①作MG⊥x轴于G,连接BM.则∠MGB=90°,设M(m,﹣m2+2m+3),
∴MG=|﹣m2+2m+3|,BG=3﹣m,
∴tan∠MBA=
223
3
m m
MG
BG m
-++
=
-
,
∵DE⊥x轴,D(1,4),∴∠DEB=90°,DE=4,OE=1,∵B(3,0),
∴BE=2,
∴tan∠BDE=BE
DE =
1
2
,
∵∠MBA=∠BDE,
∴
223
3
m m
m
-++
-
=
1
2
,
当点M在x轴上方时,
223
3
m m
m
-++
-
=
1
2
,
解得m=﹣1
2
或3(舍弃),
∴M (﹣
12,7
4
), 当点M 在x 轴下方时,
2233m m m
--- =1
2, 解得m=﹣
3
2
或m=3(舍弃), ∴点M (﹣
32,﹣9
4
), 综上所述,满足条件的点M 坐标(﹣12,74)或(﹣32,﹣9
4
); ②如图中,∵MN ∥x 轴,
∴点M 、N 关于抛物线的对称轴对称, ∵四边形MPNQ 是正方形,
∴点P 是抛物线的对称轴与x 轴的交点,即OP=1, 易证GM=GP ,即|﹣m 2+2m+3|=|1﹣m|, 当﹣m 2+2m+3=1﹣m 时,解得317
±, 当﹣m 2+2m+3=m ﹣1时,解得m=117
2
±, ∴满足条件的m 317±或
117
2
±. 【点睛】
本题考查二次函数综合题、锐角三角函数、正方形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,学会利用参数构建方程解决问题,属于中考压轴题.
5.已知,m ,n 是一元二次方程x 2+4x +3=0的两个实数根,且|m |<|n |,抛物线y =x 2+bx +c 的图象经过点A (m ,0),B (0,n ),如图所示. (1)求这个抛物线的解析式;
(2)设(1)中的抛物线与x 轴的另一个交点为抛物线的顶点为D ,求出点C ,D 的坐标,并判断△BCD 的形状;
(3)点P 是直线BC 上的一个动点(点P 不与点B 和点C 重合),过点P 作x 轴的垂线,
交抛物线于点M ,点Q 在直线BC 上,距离点P
为2个单位长度,设点P 的横坐标为t ,△PMQ 的面积为S ,求出S 与t 之间的函数关系式.
【答案】(1)2
23y x x =--;(2)C (3,0),D (1,﹣4),△BCD 是直角三角形;
(3)2213
(03)22
13(03)2
2t t t S t t t t ?-+??=??-??<<<或>
【解析】
试题分析:(1)先解一元二次方程,然后用待定系数法求出抛物线解析式;
(2)先解方程求出抛物线与x 轴的交点,再判断出△BOC 和△BED 都是等腰直角三角形,从而得到结论;
(3)先求出QF=1,再分两种情况,当点P 在点M 上方和下方,分别计算即可. 试题解析:解(1)∵2+430x x +=,∴11x =-,23x =-,∵m ,n 是一元二次方程
2+430x x +=的两个实数根,且|m|<|n|,∴m=﹣1,n=﹣3,∵抛物线2
23
y x x =--的图象经过点A (m ,0),B (0,n ),∴10{3b c c -+==-,∴2{3
b c =-=-,∴抛物线解析式为223y x x =--;
(2)令y=0,则2230x x --=,∴11x =-,23x =,∴C (3,0),
∵223y x x =--=2(1)4x --,∴顶点坐标D (1,﹣4),过点D 作DE ⊥y 轴,∵OB=OC=3,∴BE=DE=1,∴△BOC 和△BED 都是等腰直角三角形,∴∠OBC=∠DBE=45°,∴∠CBD=90°,∴△BCD 是直角三角形;
(3)如图,∵B (0,﹣3),C (3,0),∴直线BC 解析式为y=x ﹣3,∵点P 的横坐标为t ,PM ⊥x 轴,∴点M 的横坐标为t ,∵点P 在直线BC 上,点M 在抛物线上,∴P (t ,t ﹣3),M (t ,223t t --),过点Q 作QF ⊥PM ,∴△PQF 是等腰直角三角形,∵2,∴QF=1.
①当点P 在点M 上方时,即0<t <3时,PM=t ﹣3﹣(223t t --)=23t t -+,∴S=
12
PM×QF=21(3)2t t -+=213
22t t -+,②如图3,当点P 在点M 下方时,即t <0或t
>3时,PM=223t t --﹣(t ﹣3)=23t t -,∴S=
12PM×QF=12
(2
3t t -)=21322t t -.
综上所述,S=2213
(03)22
{13 (03)22
t t t t t t t 或-+<<-.
考点:二次函数综合题;分类讨论.
6.如图,在平面直角坐标系中,抛物线y=ax 2+2x+c 与x 轴交于A (﹣1,0)B (3,0)两点,与y 轴交于点C ,点D 是该抛物线的顶点. (1)求抛物线的解析式和直线AC 的解析式;
(2)请在y 轴上找一点M ,使△BDM 的周长最小,求出点M 的坐标;
(3)试探究:在拋物线上是否存在点P ,使以点A ,P ,C 为顶点,AC 为直角边的三角形是直角三角形?若存在,请求出符合条件的点P 的坐标;若不存在,请说明理由.
【答案】(1)抛物线解析式为y=﹣x 2+2x+3;直线AC 的解析式为y=3x+3;(2)点M 的坐标为(0,3);
(3)符合条件的点P 的坐标为(73,209)或(103,﹣13
9
), 【解析】
分析:(1)设交点式y=a (x+1)(x-3),展开得到-2a=2,然后求出a 即可得到抛物线解析式;再确定C (0,3),然后利用待定系数法求直线AC 的解析式;
(2)利用二次函数的性质确定D 的坐标为(1,4),作B 点关于y 轴的对称点B′,连接DB′交y 轴于M ,如图1,则B′(-3,0),利用两点之间线段最短可判断此时MB+MD 的值
最小,则此时△BDM的周长最小,然后求出直线DB′的解析式即可得到点M的坐标;(3)过点C作AC的垂线交抛物线于另一点P,如图2,利用两直线垂直一次项系数互为
负倒数设直线PC的解析式为y=-
1
3
x+b,把C点坐标代入求出b得到直线PC的解析式为
y=-1
3
x+3,再解方程组
223
1
3
3
y x x
y x
?-++
?
?
-+
??
=
=
得此时P点坐标;当过点A作AC的垂线交抛物
线于另一点P时,利用同样的方法可求出此时P点坐标.详解:(1)设抛物线解析式为y=a(x+1)(x﹣3),
即y=ax2﹣2ax﹣3a,
∴﹣2a=2,解得a=﹣1,
∴抛物线解析式为y=﹣x2+2x+3;
当x=0时,y=﹣x2+2x+3=3,则C(0,3),
设直线AC的解析式为y=px+q,
把A(﹣1,0),C(0,3)代入得
3
p q
q
-+=
?
?
=
?
,解得
3
3
p
q
=
?
?
=
?
,
∴直线AC的解析式为y=3x+3;
(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点D的坐标为(1,4),
作B点关于y轴的对称点B′,连接DB′交y轴于M,如图1,则B′(﹣3,0),
∵MB=MB′,
∴MB+MD=MB′+MD=DB′,此时MB+MD的值最小,
而BD的值不变,
∴此时△BDM的周长最小,
易得直线DB′的解析式为y=x+3,
当x=0时,y=x+3=3,
∴点M的坐标为(0,3);
(3)存在.
过点C作AC的垂线交抛物线于另一点P,如图2,
∵直线AC的解析式为y=3x+3,
∴直线PC的解析式可设为y=﹣1
3
x+b,把C(0,3)代入得b=3,
∴直线PC的解析式为y=﹣1
3
x+3,
解方程组
223
1
3
3
y x x
y x
?-++
?
?
-+
??
=
=
,解得
3
x
y
=
?
?
=
?
或
7
3
20
9
x
y
?
=
??
?
?=
??
,则此时P点坐标为(
7
3
,
20
9
);
过点A作AC的垂线交抛物线于另一点P,直线PC的解析式可设为y=﹣x+b,
把A(﹣1,0)代入得1
3
+b=0,解得b=﹣
1
3
,
∴直线PC的解析式为y=﹣1
3x﹣
1
3
,
解方程组
223
11
33
y x x
y x
?-++
?
?
--
??
=
=
,解得
1
x
y
=-
?
?
=
?
或
10
3
13
9
x
y
?
=
??
?
?=-
??
,则此时P点坐标为(
10
3
,﹣
13
9
).
综上所述,符合条件的点P的坐标为(7
3
,
20
9
)或(
10
3
,﹣
13
9
).
点睛:本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和二次函数的性质;会利用待定系数法求函数解析式,理解两直线垂直时一次项系数的关系,通过解方程组求把两函数的交点坐标;理解坐标与图形性质,会运用两点之间线段最短解决最短路径问题;会运用分类讨论的思想解决数学问题.
7.如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=﹣1.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA ⊥NA ,且PA=NA 时,求此时点P 的坐标;
②当四边形PABC 的面积最大时,求四边形PABC 面积的最大值及此时点P 的坐标.
【答案】(1)y=﹣(x+1)2+4,顶点坐标为(﹣1,4);(2)①点P 2﹣1,2);②P (﹣32
,154) 【解析】
试题分析:(1)将B 、C 的坐标代入已知的抛物线的解析式,由对称轴为1x =-即可得到抛物线的解析式;
(2)①首先求得抛物线与x 轴的交点坐标,然后根据已知条件得到PD=OA ,从而得到方程求得x 的值即可求得点P 的坐标;
②ΔOBC ΔAPD ABCP C =PDO S S S S ++四边形梯形,表示出来得到二次函数,求得最值即可.
试题解析:(1)∵抛物线2
y ax bx c =++与x 轴交于点A 和点B (1,0),与y 轴交于
点C (0,3),其对称轴l 为1x =-,∴0
{3
1
2a b c c b
a
++==-=-,解得:1
{23a b c =-=-=,∴二次函数的
解析式为2
23y x x =--+=2
(1)4x -++,∴顶点坐标为(﹣1,4);
(2)令2
230y x x =--+=,解得3x =-或1x =,∴点A (﹣3,0),B (1,0),作
PD ⊥x 轴于点D ,∵点P 在223y x x =--+上,∴设点P (x ,223x x --+), ①∵PA ⊥NA ,且PA=NA ,∴△PAD ≌△AND ,∴OA=PD ,即2232y x x =--+=,解得21(舍去)或x=21-,∴点P (21-,2);
②设P(x ,y),则223y x x =--+,∵ΔOBC ΔAPD ABCP C =PDO S S S S ++四边形梯形
=
12OB?OC+12AD?PD+12
(PD+OC)?OD=111
31+(3)(3)()222x y y x ???+++-=
333222x y -+ =2
333(23)222x x x -+--+=239622x x --+=23375()228
x -++,
∴当x=32-时,ABCP S 四边形最大值=758,当x=32
-时,2
23y x x =--+=154,此时P
(32
-
,15
4).
考点:1.二次函数综合题;2.二次函数的最值;3.最值问题;4.压轴题.
8.如图,在平面直角坐标系中,已知点B 的坐标为()1,0-,且4OA OC OB ==,抛物
线()2
0y ax bx c a =++≠图象经过,,A B C 三点.
(1)求,A C 两点的坐标; (2)求抛物线的解析式;
(3)若点P 是直线AC 下方的抛物线上的一个动点,作PD AC ⊥于点D ,当PD 的值最大时,求此时点P 的坐标及PD 的最大值.
【答案】解:(1)点A 、C 的坐标分别为(4,0)、(0,﹣4);;
(2)抛物线的表达式为:2
34y x x =﹣
﹣ ; (3)PD 有最大值,当x =2时,其最大值为2,此时点P (2,﹣6). 【解析】 【分析】
(1)OA =OC =4OB =4,即可求解;
(2)抛物线的表达式为:2
34y x x =a (x+1)(x-4)=a(﹣
﹣) ,即可求解;
(3)22
4342
--++=()
PD x x x ,即可求解. 【详解】
解:(1)OA =OC =4OB =4,
故点A 、C 的坐标分别为(4,0)、(0,﹣4);
(2)抛物线的表达式为:2
34y x x =a (x+1)(x-4)=a(﹣
﹣), 即﹣4a =﹣4,解得:a =1,
故抛物线的表达式为:234y x x --= ;
(3)直线CA 过点C ,设其函数表达式为:4y kx -=, 将点A 坐标代入上式并解得:k =1, 故直线CA 的表达式为:y =x ﹣4, 过点P 作y 轴的平行线交AC 于点H ,
∵OA =OC =4,
45OAC OCA ∴∠∠?== ,
∵//PH y 轴,
45PHD OCA ∴∠∠?==,
设点234P x x x --(,)
,则点H (x ,x ﹣4), 22
2
4342
2222
--+++=()
=-PD x x x x x
∵2
2
-
<0,∴PD 有最大值,当x =2时,其最大值为22 此时点P (2,﹣6). 【点睛】
本题考查的是二次函数综合运用,涉及到一次函数、解直角三角形、图象的面积计算等,其中(3),用函数关系表示PD ,是本题解题的关键
9.已知抛物线C1:y=ax2﹣4ax﹣5(a>0).
(1)当a=1时,求抛物线与x轴的交点坐标及对称轴;
(2)①试说明无论a为何值,抛物线C1一定经过两个定点,并求出这两个定点的坐标;
②将抛物线C1沿这两个定点所在直线翻折,得到抛物线C2,直接写出C2的表达式;(3)若(2)中抛物线C2的顶点到x轴的距离为2,求a的
值.
【答案】(1)(﹣1,0)或(5,0)(2)①(0,﹣5),(4,﹣5)②y=﹣ax2+4ax﹣5(3)a=或
【解析】
试题分析:(1)将a=1代入解析式,即可求得抛物线与x轴交点;
(2)①化简抛物线解析式,即可求得两个点定点的横坐标,即可解题;
②根据抛物线翻折理论即可解题;
(3)根据(2)中抛物线C2解析式,分类讨论y=2或﹣2,即可解题
试题解析:(1)当a=1时,抛物线解析式为y=x2﹣4x﹣5=(x﹣2)2﹣9,
∴对称轴为y=2;
∴当y=0时,x﹣2=3或﹣3,即x=﹣1或5;
∴抛物线与x轴的交点坐标为(﹣1,0)或(5,0);
(2)①抛物线C1解析式为:y=ax2﹣4ax﹣5,
整理得:y=ax(x﹣4)﹣5;
∵当ax(x﹣4)=0时,y恒定为﹣5;
∴抛物线C1一定经过两个定点(0,﹣5),(4,﹣5);
②这两个点连线为y=﹣5;
将抛物线C1沿y=﹣5翻折,得到抛物线C2,开口方向变了,但是对称轴没变;
∴抛物线C2解析式为:y=﹣ax2+4ax﹣5,
(3)抛物线C2的顶点到x轴的距离为2,
则x=2时,y=2或者﹣2;
当y=2时,2=﹣4a+8a﹣5,解得,a=;
当y=﹣2时,﹣2=﹣4a+8a ﹣5,解得,a=;
∴a=
或
;
考点:1、抛物线与x 轴的交点;2、二次函数图象与几何变换
10.某大学生利用暑假40天社会实践参与了一家网店经营,了解到一种成本为20元/件的新型商品在第x 天销售的相关信息如下表所示. 销售量p (件)
P=50—x
销售单价q (元/件)
当1≤x≤20时,1q 30x 2=+
当21≤x≤40时,525
q 20x
=+
(1)请计算第几天该商品的销售单价为35元/件? (2)求该网店第x 天获得的利润y 关于x 的函数关系式. (3)这40天中该网店第几天获得的利润最大?最大利润是多少? 【答案】(1)第10天或第35天该商品的销售单价为35元/件(2)
()()21
x 15x 5001x 202y {26250
52521x 40x
-++≤≤=-≤≤(3)这40天中该网店第21天获得的利润最大?最
大利润是725元 【解析】 【分析】
(1)分别将q=35代入销售单价关于x 的函数关系式,求出x 即可. (2)应用利润=销售收入-销售成本列式即可.
(3)应用二次函数和反比例函数的性质,分别求出最大值比较即得所求. 【详解】
解:(1)当1≤x≤20时,令1
q 30x 352
=+=,解得;x 10=; 当21≤x≤40时,令525
q 2035x
=+
=,解得;x 35=. ∴第10天或第35天该商品的销售单价为35元/件.
(2)当1≤x≤20时,()211y 30x 2050x x 15x 50022??
=+--=-++ ???
;
当21≤x≤40时,()52526250y 202050x 525x x ??
=+
--=- ???
. ∴y 关于x 的函数关系式为()()21
x 15x 5001x 202
y {26250
52521x 40x
-++≤≤=-≤≤.
(3)当1≤x≤20时,()2
211y x 15x 500x 15612.522
=-++=--+, ∵1
02
-
<,∴当x=15时,y 有最大值y 1,且y 1=612.5. 当21≤x≤40时,∵26250>0,∴26250
x
随着x 的增大而减小, ∴当x=21时,26250y 525x =-有最大值y 2,且226250
y 52572521
=-=. ∵y 1<y 2,
∴这40天中该网店第21天获得的利润最大?最大利润是725元.
水尾中学中考专项训练(压轴题)答案 1.(四川模拟)如图,Rt △ABC 内接于⊙O ,∠ACB =90°,AC =23,BC =1.以AC 为一边,在AC 的右侧作等边△ACD ,连接BD ,交⊙O 于点E ,连接AE ,求BD 和AE 的长. 解:过D 作DF ⊥BC ,交BC 的延长线于F ∵△ACD 是等边三角形 ∴AD =CD =AC =23,∠ACD =60° ∵∠ACB =90°,∴∠ACF =90° ∴∠DCF =30°,∴DF = 1 2 CD =3,CF =3DF =3 ∴BF =BC +CF =1+3=4 ∴BD = BF 2 +DF 2 = 16+3 =19 ∵AC =23,BC =1,∴AB = AC 2 +BC 2 = 13 ∵BE +DE =BD ,∴AB 2 -AE 2 + AD 2 -AE 2 =BD 即 13-AE 2 + 12-AE 2 =19 ∴13-AE 2 =19- 12-AE 2 两边平方得:13-AE 2=19+12-AE 2-2 19(12-AE 2 ) 整理得:19(12-AE 2 ) =9,解得AE = 7 19 57 2.(四川模拟)已知Rt △ABC 中,∠ACB =90°,∠B =60°,D 为△ABC 外接圆⊙O 上 AC ︵ 的中点. (1)如图1,P 为 ABC ︵ 的中点,求证:PA +PC =3PD ; (2)如图2,P 为 ABC ︵ 上任意一点,(1)中的结论还成立吗?请说明理由. (1)证明:连接AD ∵D 为AC ︵ 的中点,P 为 ABC ︵ 的中点 ∴PD 为⊙O 的直径,∴∠PAD =90° D D P 图1 图2
二次函数与圆 1、如图,AB 是⊙O 的直径,弦BC=2cm ,∠ABC=60o. (1)求⊙O 的直径; (2)若D 是AB 延长线上一点,连结CD ,当BD 长为多少时,CD 与⊙O 相切; (3)若动点E 以2cm/s 的速度从A 点出发沿着AB 方向运动,同时动点F 以1cm/s 的 速度从B 点出发沿BC 方向运动,设运动时间为)20)((< 2、如图,在平面直角坐标系中,顶点为(4,﹣1)的抛物线交y轴于A点,交x轴于B,C两点(点B在点C的左侧),已知A点坐标为(0,3). (1)求此抛物线的解析式 (2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有怎样的位置关系,并给出证明; (3)已知点P是抛物线上的一个动点,且位于A,C两点之间,问:当点P运动到什么位置时,△PAC的面积最大?并求出此时P点的坐标和△PAC的最大面积. 3、如图,抛物线2 23y x x =-++与x 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为D . (1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴; (2)连接BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作 PF DE ∥交抛物线于点F ,设点P 的横坐标为m ; ①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形? ②设BCF △的面积为S ,求S 与m 的函数关系式. 【例1】.如图,点()40M ,,以点M 为圆心、2为半径的圆与x 轴交于点A B ,.已知抛物 21 6 y x bx c =++过点A 和B ,与y 轴交于点C . ⑴ 求点C 的坐标,并画出抛物线的大致图象. ⑵ 点()8Q m ,在抛物线21 6 y x bx c =++上,点P 为此抛物线对称轴上一个动点,求 PQ PB + 最小值. ⑶ CE 是过点C 的M ⊙的切线,点E 是切点,求OE 所在直线的解析式. 【巩固】已知抛物线2y ax bx c =++与y 轴的交点为C ,顶点为M ,直线CM 的解析式 2y x =-+并且线段CM 的长为(1)求抛物线的解析式。 (2)设抛物线与x 轴有两个交点A (X 1 ,0)、B (X 2 ,0),且点A 在B 的左侧,求线段AB 的长。 (3)若以AB 为直径作⊙N ,请你判断直线CM 与⊙N 的位置关系,并说明理由。 【例2】如图,在平面直角坐标系中,以点(04)C ,为圆心,半径为4的圆交y 轴正半轴于点A , AB 是C ⊙的切线. 动点P 从点A 开始沿AB 方向以每秒1个单位长度的速度运动,点Q 从O 点开始沿x 轴正方向以每秒4个单位长度的速度运动,且动点P 、 Q 从点A 和点O 同时出发,设运动时间为t (秒). ⑴当1t =时,得到1P 、1Q 两点,求经过A 、1P 、1Q 三点的抛物线解析式及对称轴l ; ⑵当t 为何值时,直线PQ 与C ⊙相切?并写出此时点P 和点Q 的坐标; ⑶在⑵的条件下,抛物线对称轴l 上存在一点N ,使NP NQ +最小,求出点N 的坐标并说明理由. 提示:(1)先求出t=1时,AP 和OQ 的长,即可求得P 1,Q 1的坐标,然后用待定系数法即可得出抛物线的解析式.进而可求出对称轴l 的解析式. (2)当直线PQ 与圆C 相切时,连接CP ,CQ 则有Rt △CMP ∽Rt △QMC (M 为PG 与圆的切点),因此可设当t=a 秒时,PQ 与圆相切,然后用a 表示出AP ,OQ 的长即PM ,QM 的长(切线长定理).由此可求出a 的值. (3)本题的关键是确定N 的位置,先找出与P 点关于直线l 对称的点P ′的坐标,连接P ′Q ,那么P ′Q 与直线l 的交点即为所求的N 点,可先求出直线P ′Q 的解析式,进而可求出N 点的坐标. 【巩固】已知二次函数图象的顶点在原点O ,对称轴为y 轴.一次函数1y kx =+的图象与 二次函数的图象交于A B ,两点(A 在B 的左侧),且A 点坐标为()44-,.平行于x 轴的直线 l 过()01-,点. ⑴ 求一次函数与二次函数的解析式; ⑵ 判断以线段AB 为直径的圆与直线l 的位置关系,并给出证明; ⑶ 把二次函数的图象向右平移2个单位,再向下平移t 个单位()0t >,二次函数的图象与x 二次函数基础练习题 练习一 二次函数 1、 一个小球由静止开始在一个斜坡上向下滚动,通过仪器观察得到 小球滚动的距离s (米)与时间t (秒)的数据如下表: 写出用t 表示s 的函数关系式: 2、 下列函数:① 23 y x ;② 21y x x x ;③ 224y x x x ;④ 2 1 y x x ; ⑤ 1y x x ,其中是二次函数的是 ,其中a ,b ,c 3、当m 时,函数2235y m x x (m 为常数)是关于x 的二次函数 4、当____m 时,函数2221m m y m m x 是关于x 的二次函数 5、当____m 时,函数2564m m y m x +3x 是关于x 的二次函数 6、若点 A ( 2, m ) 在函数 12-=x y 的图像上,则 A 点的坐标是____. 7、在圆的面积公式 S =πr 2 中,s 与 r 的关系是( ) A 、一次函数关系 B 、正比例函数关系 C 、反比例函数关系 D 、二次函数关系 8、正方形铁片边长为15cm ,在四个角上各剪去一个边长为x (cm )的小正方形,用余下的部分做成一个无盖的盒子. (1)求盒子的表面积S (cm 2)与小正方形边长x (cm )之间的函数关系式; (2)当小正方形边长为3cm 时,求盒子的表面积. 9、如图,矩形的长是 4cm ,宽是 3cm ,如果将长和宽都增加 x cm , 那么面积增加 ycm 2, ① 求 y 与 x 之间的函数关系式. ② 求当边长增加多少时,面积增加 8cm 2. 10、已知二次函数),0(2≠+=a c ax y 当x=1时,y= -1; 当x=2时,y=2,求该函数解析式. 11、富根老伯想利用一边长为a 米的旧墙及可以围 成24米长的旧木料,建造猪舍三间,如图,它们的平 面图是一排大小相等的长方形. (1) 如果设猪舍的宽AB 为x 米,则猪舍的总面积S (米2)与x 有怎 样的函数关系? (2) 请你帮富根老伯计算一下,如果猪舍的总面积为32米2,应该如 何安排猪舍的长BC 和宽AB 的长度?旧墙的长度是否会对猪舍 图6 x y F E H N M P D C B A O 二次函数和圆 【例题1】 (芜湖市) 已知圆P 的圆心在反比例函数k y x = (1)k >图象上,并与x 轴相交于A 、B 两点. 且始终与y 轴相切于定点C (0,1). (1) 求经过A 、B 、C 三点的二次 函数图象的解析式; (2) 若二次函数图象的顶点为 D ,问当k 为何值时,四边形ADBP 为菱形. 【例题2】(湖南省韶关市) 25.如图6,在平面直角坐标系中,四边形OABC 是矩形,OA=4,AB=2,直线3 2 y x =-+ 与坐标轴交于D 、E 。设M 是AB 的中点,P 是线段DE 上的动点. (1)求M 、D 两点的坐标; (2)当P 在什么位置时,PA=PB ?求出此时P 点的坐标; (3)过P 作PH ⊥BC ,垂足为H ,当以PM 为直径的⊙F 与BC 相切于点N 时,求梯形PMBH 的面积. 【例题3】(甘肃省白银等7市新课程)28. 在直角坐标系中,⊙A的半径为4,圆心A的坐标为(2,0),⊙A与x轴交于E、F两点,与y轴交于C、D两点,过点C作⊙A的切线BC,交x轴于点B. (1)求直线CB的解析式; (2)若抛物线y=ax2+b x+c的顶点在直线BC上,与x 轴的交点恰为点E、F,求该抛物线的解析式; (3)试判断点C是否在抛物线上? (4)在抛物线上是否存在三个点,由它构成的三角形与 △AOC相似?直接写出两组这样的点. 【例题4】(绵阳市)25.如图,已知抛物线y = ax2 + bx-3与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为5.设⊙M与y轴交于D,抛物线的顶点为E. (1)求m的值及抛物线的解析式; (2)设∠DBC = α,∠CBE = β,求sin(α-β)的值; (3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE相似?若存在,请指出点P的位置,并直接写出点P的坐标;若不存在,请说明理由. 【例题5】(南充市)25.如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A、 第05练 二次函数与幂函数 刷基础 1.(2020·贵溪市实验中学高二期末)已知函数( ) 2 53 ()1m f x m m x --=--是幂函数且是(0,)+∞上的增函数, 则m 的值为( ) A .2 B .-1 C .-1或2 D .0 【答案】B 【解析】 由题意得2 11,530,1m m m m --=-->∴=-, 故选:B. 2.(2020·浙江高一课时练习)如图,函数1y x = 、y x =、1y =的图象和直线1x =将平面直角坐标系的第一象限分成八个部分:①②③④⑤⑥⑦⑧.若幂函数 的图象经过的部分是④⑧,则 可能是( ) A .y =x 2 B .y x = C .12 y x = D .y=x -2 【答案】B 【解析】 由图象知,幂函数()f x 的性质为: (1)函数()f x 的定义域为()0+∞, ; (2)当01x <<时,()1f x >,且()1f x x <;当1x >时,01x <<,且()1 f x x >; 所以()f x 可能是y x = .故选B. 3.(2019·河南高三月考)若e a =π,3e b =,3c π=,则a ,b ,c 的大小关系为( ) A .b a c << B .a b c << C .c a b << D .b c a << 【答案】A 【解析】 因为3x y =在R 上为增函数,所以33e π<,即b c <. 因为e y x =在(0,)+∞为增函数,所以3e e π>,即a b >. 设ln ()x f x x = , 2 1ln ()x f x x -'= ,令()0f x '=,x e =. (0,)x e ∈,()0f x '>,()f x 为增函数, (,)x e ∈+∞,()0f x '<,()f x 为减函数. 则()(3)f f π<,即 ln ln 3 3 π π < ,因此3ln ln3ππ<, 即3ln ln 3ππ<,33ππ<.又33e πππ<<,所以a c <. 所以b a c <<. 故选:A 4.(2020·全国高一专题练习)下列关系中正确的是( ) A .2213 3 3 111252??????<< ? ? ? ?????? B .122333 111225??????<< ? ? ? ?????? C .212333 111522??????<< ? ? ? ?????? D .221333 111522??????<< ? ? ? ?????? 【答案】D 【解析】 因为12x y ??= ???是单调递减函数,1233<,所以12 331122????> ? ????? , 因为幂函数23y x =在()0,∞+上递增,11 52 <; 所以223 3 1152????< ? ? ???? , 圆与二次函数综合题 1、已知:二次函数y=x2-kx+k+4的图象与y轴交于点c,且与x轴的正半轴交于A、B两点(点A 在点B左侧)。若A、B两点的横坐标为整数。 (1)确定这个二次函数的解析式并求它的顶点坐标;(2)若点D的坐标是(0,6),点P(t,0)是线段AB上的一个动点,它可与点A重合,但不与点B重合。设四边形PBCD的面积为S,求S与t的函数关系式; (3)若点P与点A重合,得到四边形ABCD,以四边形ABCD的一边为边,画一个三角形,使它的面积等于四边形ABCD的面积,并注明三角形高线的长。再利用“等底等高的三角形面积相等”的知识,画一个三角形,使它的面积等于四边形ABCD的面积(画示意图,不写计算和证明过程)。 2、(1)已知:关于x、y的方程组有两个实数解,求m的取值范围; (2)在(1)的条件下,若抛物线y=-(m-1)x2+(m-5)x+6与x轴交于A、B两点,与y轴交于点C,且△ABC的面积等于12,确定此抛物线及直线y=(m+1)x-2的解析式; (3)你能将(2)中所得的抛物线平移,使其顶点在(2)中所得的直线上吗?请写出一种平移方法。 3、已知:二次函数y=x2-2(m-1)x+m2-2m-3,其中m为实数。 (1)求证:不论m取何实数,这个二次函数的图像与x轴必有两个交点;(2)设这个二次函数的图像与x轴交于点A(x1,0)、B(x2,0),且x1、x2的倒数和为,求这个二次函数的解析式。 4、已知二次函数y1=x2-2x-3. (1)结合函数y1的图像,确定当x取什么值时,y1>0,y1=0,y1<0; (2)根据(1)的结论,确定函数y2= (|y1|-y1)关于x的解析式; (3)若一次函数y=kx+b(k 0)的图像与函数y2的图像交于三个不同的点,试确定实数k与b应满足的条件。 5、已知:如图,直线y= x+ 与x轴、y轴分别交于A、B两点,⊙M经过原点O及A、B两点。 (1)求以OA、OB两线段长为根的一元二次方程; (2)C是⊙M上一点,连结BC交OA于点D,若∠COD=∠CBO, 写出经过O、C、A三点的二次函数的解析式; (3)若延长BC到E,使DE=2,连结EA,试判断直线EA与 ⊙M的位置关系,并说明理由。(河南省) 6、如图,已知点A(tan ,0)B(tan ,0)在x轴正半轴上,点A在点B的左 边,、是以线段AB为斜边、顶点C在x轴上方的Rt△ABC的两个锐角。 (1)若二次函数y=-x2- 5/2kx+(2+2k-k2)的图像经过A、B两点,求它的解析式; (2)点C在(1)中求出的二次函数的图像上吗?请说明理由。(陕西省) 题型04 二次函数的实际应用题 一、单选题 1.如图,隧道的截面由抛物线和长方形OABC 构成,长方形的长OA 是12m ,宽OC 是4m .按照图中所示的平面直角坐标系,抛物线可以用y =﹣ 16 x 2 +bx +c 表示.在抛物线型拱璧上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m .那么两排灯的水平距离最小是( ) A .2m B .4m C . D .【答案】D 【分析】根据长方形的长OA 是12m ,宽OC 是4m ,可得顶点的横坐标和点C 的坐标,即可求出抛物线解析式,再把y =8代入解析式即可得结论. 【详解】根据题意,得 OA =12,OC =4. 所以抛物线的顶点横坐标为6, 即﹣2b a =13 b =6,∴b =2. ∵C (0,4),∴c =4, 所以抛物线解析式为: y =﹣ 16 x 2 +2x +4 =﹣ 16 (x ﹣6)2 +10 当y =8时, 8=﹣ 1 6 (x ﹣6)2+10, 解得:x 1 x 2=6﹣ 则x 1﹣x 2 . 所以两排灯的水平距离最小是 43. 故选:D. 【点睛】本题考查了二次函数的应用,解决本题的关键是把实际问题转化为二次函数问题解决. 2.使用家用燃气灶烧开同一壶水所需的燃气量y(单位:m3)与旋钮的旋转角度x(单位:度)(0°<x≤90°)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用节能燃气灶烧开同一壶水的旋钮的旋转角度x 与燃气量y的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮的旋转角度约为() A.33°B.36°C.42°D.49° 【答案】C 【分析】据题意和二次函数的性质,可以确定出对称x的取值范围,从而可以解答本题. 【详解】解:由图象可知,物线开口向上, 该函数的对称轴x>1854 2 且x<54, ∴36<x<54, 即对称轴位于直线x=36与直线x=54之间且靠近直线x=36, 故选:C. 【点睛】本题考查二次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解答. 3.某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是() 二次函数综合问题例谈 二次函数是中学代数的基本内容之一,它既简单又具有丰富的内涵和外延. 作为最基本的初等函数,可以以它为素材来研究函数的单调性、奇偶性、最值等性质,还可建立起函数、方程、不等式之间的有机联系;作为抛物线,可以联系其它平面曲线讨论相互之间关系. 这些纵横联系,使得围绕二次函数可以编制出层出不穷、灵活多变的数学问题. 同时,有关二次函数的内容又与近、现代数学发展紧密联系,是学生进入高校继续深造的重要知识基础. 因此,从这个意义上说,有关二次函数的问题在高考中频繁出现,也就不足为奇了. 学习二次函数,可以从两个方面入手:一是解析式,二是图像特征. 从解析式出发,可以进行纯粹的代数推理,这种代数推理、论证的能力反映出一个人的基本数学素养;从图像特征出发,可以实现数与形的自然结合,这正是中学数学中一种非常重要的思想方法. 本文将从这两个方面研究涉及二次函数的一些综合问题. 1. 代数推理 由于二次函数的解析式简捷明了,易于变形(一般式、顶点式、零点式等),所以,在解决二次函数的问题时,常常借助其解析式,通过纯代数推理,进而导出二次函数的有关性质. 1.1 二次函数的一般式c bx ax y ++=2 )0(≠c 中有三个参数c b a ,,. 解题的关键在于:通过三个独立条件“确定”这三个参数. 例1 已知f x ax bx ()=+2 ,满足1≤-≤f ()12且214≤≤f (),求f ()-2的取值范围. 分析:本题中,所给条件并不足以确定参数b a ,的值,但应该注意到:所要求的结论不是()2-f 的确定值,而是与条件相对应的“取值范围”,因此,我们可以把1≤-≤f ()12和 4)1(2≤≤f 当成两个独立条件,先用()1-f 和()1f 来表示b a ,. 解:由()b a f +=1,()b a f -=-1可解得: ))1()1((2 1 )),1()1((21--=-+= f f b f f a (*) 将以上二式代入f x ax bx ()=+2 ,并整理得 ()()??? ? ??--+???? ??+=2)1(2122x x f x x f x f , ∴ ()()()1312-+=f f f . 又∵214≤≤f (),2)1(1≤-≤f , ∴ ()1025≤≤f . 二次函数与圆综合提高(压轴题) 1、如图,在等边△ABC中,AB=3,D、E分别是AB、AC上的点, 且DE∥BC,将△ADE沿DE翻折,与梯形BCED重叠的部分记作图 形L. (1)求△ABC的面积; (2)设AD=x,图形L的面积为y,求y关于x的函数解析式; (3)已知图形L的顶点均在⊙O上,当图形L的面积最大时,求⊙O的面积.解 解:(1)如图3,作AH⊥BC于H, 答: ∴∠AHB=90°. ∵△ABC是等边三角形, ∴AB=BC=AC=3. ∵∠AHB=90°, ∴BH=BC= 在Rt△ABC中,由勾股定理,得 AH=. ∴S△ABC==; (2)如图1,当0<x≤1.5时,y=S△ADE. 作AG⊥DE于G, ∴∠AGD=90°,∠DAG=30°, ∴DG=x,AG=x, ∴y==x2, ∵a=>0,开口向上,在对称轴的右侧y随x的增大而增大, ∴x=1.5时,y 最大=, 如图2,当1.5<x<3时,作MG⊥DE于G, ∵AD=x, ∴BD=DM=3﹣x, ∴DG=(3﹣x),MF=MN=2x﹣3, ∴MG=(3﹣x), ∴y=, =﹣; (3),如图4,∵y=﹣; ∴y=﹣(x2﹣4x)﹣, y=﹣(x﹣2)2+, ∵a=﹣<0,开口向下, ∴x=2时,y最大=, ∵>, ∴y最大时,x=2, ∴DE=2,BD=DM=1.作FO⊥DE于O,连接MO,ME.∴DO=OE=1, ∴DM=DO. ∵∠MDO=60°, ∴△MDO是等边三角形, ∴∠DMO=∠DOM=60°,MO=DO=1. ∴MO=OE,∠MOE=120°, ∴∠OME=30°, ∴∠DME=90°, ∴DE是直径, S⊙O=π×12=π. 2、(2013?压轴题)如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(0,4), 点B的坐标为(4, 0),点C的坐标为 (﹣4,0),点P在 射线AB上运动,连 结CP与y轴交于点 D,连结BD.过P, D,B三点作⊙Q与 y轴的另一个交点 为E,延长DQ交⊙Q于点F,连结EF,BF. (1)求直线AB的函数解析式; (2)当点P在线段AB(不包括A,B两点)上时. ①求证:∠BDE=∠ADP; ②设DE=x,DF=y.请求出y关于x的函数解析式; (3)请你探究:点P在运动过程中,是否存在以B,D,F为顶点的直角三角形,满足两条直角边之比为2:1?如果存在,求出此时点P的坐标:如果不存在,请说明理由. 解:(1)设直线AB的函数解析式为y=kx+4, 代入(4,0)得:4k+4=0, 解得:k=﹣1, 则直线AB的函数解析式为y=﹣x+4; (2)①由已知得: OB=OC,∠BOD=∠COD=90°, 又∵OD=OD, ∴△BOD≌△COD, 二次函数和圆 【例题1】 (芜湖市) 已知圆P 的圆心在反比例函数k y x = (1)k >图象上,并与x 轴相交于A 、B 两点. 且始终与y 轴相切于定点C (0,1). (1) 求经过A 、B 、C 三点的二 次函数图象的解析式; (2) 若二次函数图象的顶点为D , 问当k 为何值时,四边形ADBP 为菱形. 【例题2】(湖南省韶关市) 25.如图6,在平面直角坐标系中,四边形OABC 是矩形,OA=4,AB=2,直线32 y x =-+ 与坐标轴交于D 、E 。设M 是AB 的中点,P 是线段DE 上的动点. (1)求M 、D 两点的坐标; (2)当P 在什么位置时,PA=PB ?求出此时P 点的坐标; (3)过P 作PH ⊥BC ,垂足为H ,当以PM 为直径的⊙F 与BC 相切于点N 时,求梯形PMBH 的面积. 【例题3】(甘肃省白银等7市新课程)28. 在直角坐标系中,⊙A的半径为4,圆心A的坐标为(2,0),⊙A与x轴交于E、F两点,与y轴交于C、D两点,过点C作⊙A的切线BC,交x轴于点B. (1)求直线CB的解析式; (2)若抛物线y=ax2+b x+c的顶点在直线BC上,与x 轴的交点恰为点E、F,求该抛物线的解析式; (3)试判断点C是否在抛物线上? (4)在抛物线上是否存在三个点,由它构成的三角形与 △AOC相似?直接写出两组这样的点. 【例题4】(绵阳市)25.如图,已知抛物线y = ax2 + bx-3与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为5.设⊙M与y轴交于D,抛物线的顶点为E. (1)求m的值及抛物线的解析式; (2)设∠DBC = α,∠CBE = β,求sin(α-β)的值; (3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE相似?若存在,请指出点P的位置,并直接写出点P的坐标;若不存在,请说明理由. 【例题5】(南充市)25.如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A、B.已 专题63 构造圆与隐形圆在二次函数中的综合问题 1、如图,在直角坐标系中,直线y=﹣1 3x ﹣1与x 轴,y 轴的交点分别为A 、B ,以x=﹣1为对称轴的抛物线 y=x 2+bx+c 与x 轴分别交于点A 、C ,直线x=﹣1与x 轴交于点D . (1)求抛物线的解析式; (2)在线段AB 上是否存在一点P ,使以A ,D ,P 为顶点的三角形与△AOB 相似?若存在,求出点P 的坐标;如果不存在,请说明理由; (3)若点Q 在第三象限内,且tan△AQD=2,线段CQ 是否存在最小值,如果存在直接写出最小值;如果不存在,请说明理由. 【答案】(1)y=x 2+2x ﹣3;(2)存在;点P 坐标为(﹣1,?23 )或(-65 ,-3 5 ); (3)存在,CQ 最小值为 √37?√5 2 . 【解析】(1)△直线y=﹣1 3x ﹣1与x 轴交于A 点, △点A 坐标为(﹣3,0), 又△直线x=﹣1为对称轴, △点C 坐标为(1,0), △抛物线解析式为:y=(x+3)(x ﹣1)=x 2+2x ﹣3; (2)存在; 由已知,点D 坐标为(﹣1,0),点B 坐标为(0,﹣1), 设点P 的坐标为(a ,﹣13 a ﹣1), △当△AOB△△ADP 时, AD AO = DP OB ,即23 = 1 3 a+11 , 解得:a=﹣1; 点P 坐标为(﹣1,?2 3); △当△AOB△△APD 时, 过点P 作PE△x 轴于点E , 则△APE△△PED , △PE 2=AE?ED , △(﹣1 3a ﹣1)2=(a+3)(﹣a ﹣1), 解得a 1=﹣3(舍去),a 2=﹣6 5, △点P 坐标为(﹣6 5 ,﹣3 5 ); (3)存在,CQ 最小值为 √37?√5 2 ; 如图,取点F (﹣1,﹣1),过点ADF 作圆,则点E (﹣2,﹣1 2)为圆心, 高考数学复习二次函数测试题 1.解析式、待定系数法 若()2 f x x bx c =++,且()10f =,()30f =,求()1f -的值. 变式1:若二次函数()2 f x ax bx c =++的图像的顶点坐标为()2,1-,与y 轴的交点坐标为 (0,11),则 A .1,4,11a b c ==-=- B .3,12,11a b c === C .3,6,11a b c ==-= D .3,12,11a b c ==-= 变式2:若()()2 23,[,]f x x b x x b c =-+++∈的图像x =1对称,则c =_______. 变式3:若二次函数()2 f x ax bx c =++的图像与x 轴有两个不同的交点()1,0A x 、 ()2,0B x ,且2212269 x x += ,试问该二次函数的图像由()()2 31f x x =--的图像向上平移几个单位得到? 2.图像特征 将函数()2 361f x x x =--+配方,确定其对称轴,顶点坐标,求出它的单调区间及最大值 或最小值,并画出它的图像. 变式1:已知二次函数()2 f x ax bx c =++,如果()()12f x f x =(其中12x x ≠),则 122x x f +??= ??? A .2b a - B .b a - C . c D .244ac b a - 变式2:函数()2 f x x px q =++对任意的x 均有()()11f x f x +=-,那么()0f 、()1f -、 ()1f 的大小关系是 A .()()()110f f f <-< B .()()()011f f f <-< C .()()()101f f f <<- D .()()()101f f f -<< 变式3:已知函数()2 f x ax bx c =++的图像如右图所示, 请至少写出三个与系数a 、b 、c 有关的正确命题_________. 3.单调性 x y O 圆与二次函数综合题 1.已知圆P 的圆心在反比例函数k y x =(1)k >图象上,并与x 轴相交于A 、B 两点. 且始终与y 轴相切于定点C (0,1). (1) 求经过A 、B 、C 三点的二次 函数图象的解析式; (2) 若二次函数图象的顶点为 D ,问当k 为何值时,四边形ADBP 为菱形. 2.如图6,在平面直角坐标系中,四边形OABC 是矩形,OA=4,AB=2,直线32 y x =-+ 与坐标轴交于D 、E 。设M 是AB 的中点,P 是线段DE 上的动点. (1)求M 、D 两点的坐标; (2)当P 在什么位置时,PA=PB ?求出此时P 点的坐标; (3)过P 作PH ⊥BC ,垂足为H ,当以PM 为直径的⊙F 与BC 相切于点N 时,求梯形PMBH 的 面积. (3) (2) 3.如图,已知抛物线y = ax 2 + bx -3与x 轴交于A 、B 两点,与y 轴交于C 点,经过A 、B 、 C 三点的圆的圆心M (1,m )恰好在此抛物线的对称轴上,⊙M 的半径为5.设⊙M 与y 轴 交于D ,抛物线的顶点为E . (1)求m 的值及抛物线的解析式; (2)设∠DBC = α,∠CBE = β,求sin (α-β)的值; (3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE相似?若存在,请指出点P的位置,并直接写出点P的坐标;若不存在,请说明理由. 4.如图,点P在y轴上,半径为3的⊙P分别交x轴于A、B两点,AB=4,交y轴负半轴于点C,连接AP并延长交⊙P于点D,过D作⊙P的切线分别交x轴、y轴于点F、G; (1)求直线FG的解析式; (2)连接CD交AB于点E,求PCD ∠ tan的值; (3)设M是劣弧BC上的一个动点,连接DM交x轴于点N,问:是否存在这样的一个常数k,始终满足AN·AB+DN·DM=K,如果存在,请求出K的值,如果不存在,请说明理由; (图1) (图2) 5.已知:如图, 抛物线2 33 y x x =--x轴分别交于A B ,两点,与y轴交于C点,M经过原点O及点A C ,,点D是劣弧OA上一动点(D点与A O ,不重合).(1)求抛物线的顶点E的坐标;(2)求M的面积; (3)连CD交AO于点F,延长CD至G,使2 FG=,试探究当点D运动到何处时,直线GA与M相切,并请说明理由. 6.(0) A m,(0) m<,以AB为边在x轴下方作正方形ABCD,点E是线段OD与正方形ABCD的外接圆除点D以外的另一个交点,连结BE与AD相交于点F. (1)求证:BF DO =; (2)设直线l是BDO △的边BO的垂直平分线,且与BE相交于点G.若G是BDO △的 秒杀二次函数综合问题(高考专题) 二次函数是中学代数的基本内容之一,它既简单又具有丰富的内涵和外延. 作为最基本的初等函数,可以以它为素材来研究函数的单调性、奇偶性、最值等性质,还可建立起函数、方程、不等式之间的有机联系;作为抛物线,可以联系其它平面曲线讨论相互之间关系. 这些纵横联系,使得围绕二次函数可以编制出层出不穷、灵活多变的数学问题. 同时,有关二次函数的内容又与近、现代数学发展紧密联系,是学生进入高校继续深造的重要知识基础. 因此,从这个意义上说,有关二次函数的问题在高考中频繁出现,也就不足为奇了. 学习二次函数,可以从两个方面入手:一是解析式,二是图像特征. 从解析式出发,可以进行纯粹的代数推理,这种代数推理、论证的能力反映出一个人的基本数学素养;从图像特征出发,可以实现数与形的自然结合,这正是中学数学中一种非常重要的思想方法. 本文将从这两个方面研究涉及二次函数的一些综合问题. 1. 代数推理 由于二次函数的解析式简捷明了,易于变形(一般式、顶点式、零点式等),所以,在解决二次函数的问题时,常常借助其解析式,通过纯代数推理,进而导出二次函数的有关性质. 1.1 二次函数的一般式c bx ax y ++=2 )0(≠c 中有三个参数c b a ,,. 解题的关键在于:通过三个独立条件“确定”这三个参数. 例1 已知,满足1 且 ,求 的取值 范围. 分析:本题中,所给条件并不足以确定参数b a ,的值,但应该注意到:所要求的结论不是()2-f 的确定值,而是与条件相对应的“取值范围”,因此,我们可以把1 和 4)1(2≤≤f 当成两个独立条件,先用()1-f 和()1f 来表示b a ,. 解:由()b a f +=1,()b a f -=-1可解得: ))1()1((2 1 )),1()1((21--=-+= f f b f f a (*) 将以上二式代入 ,并整理得 ()()??? ? ??--+???? ??+=2)1(2122x x f x x f x f , ∴ ()()()1312-+=f f f . 又∵ ,2)1(1≤-≤f , ∴ ()1025≤≤f . 例2 设 ,若 ,,, 试证 中考专题: 圆与函数综合题 1、如图,平面直角坐标系中,以点C (22为半径的圆与轴交于A 、B 两点. (1)求A 、B 两点的坐标; (2)若二次函数2y x bx c =++的图象经过点A 、B ,试确定此二次函数的解析式. 2、如图,半径为2的⊙C 与x 轴的正半轴交于点A ,与y 轴的正半轴交于点B ,点C 的坐标为(1, 0).若抛物线2 3 y x bx c =++过A 、B 两点. (1)求抛物线的解析式; (2)在抛物线上是否存在点P ,使得∠PBO=∠POB ?若存在,求出点P 的坐标;若不存在说明理由; (3)若点M 是抛物线(在第一象限内的部分)上一点,△MAB 的面积为S ,求S 的最大(小)值. 3、如图,抛物线2y ax bx c =++的对称轴为轴,且经过(0,01 16 )两点,点P 在抛物线上运动,以P 为圆心的⊙P 经过定点A (0,2), (1)求a,b,c 的值; (2)求证:点P 在运动过程中,⊙P 始终与轴相交; (3)设⊙P 与轴相交于M ()1x ,0,N ()()21 2x ,0x x 两点,当△AMN 为等腰三角形时,求圆心P 的纵坐标。 4、如图,二次函数y =x 2 +bx -3b +3的图象与x 轴交于A 、B 两点(点A 在点B 的左边),交y 轴于 点C ,且经过点(b -2,2b 2 -5b -1). (1)求这条抛物线的解析式; (2)⊙M 过A 、B 、C 三点,交y 轴于另一点D ,求点M 的坐标; (3)连接AM 、DM ,将∠AMD 绕点M 顺时针旋转,两边MA 、MD 与x 轴、y 轴分别交于点E 、F ,若△DMF 为等腰三角形,求点E 的坐标. 2019 初三数学中考专题复习 二次函数和圆 专题综合检测 1.下列关系式中,属于二次函数的是(x 为自变量)( ) =18x 2 =-x 2 -1 =1x 2 =a 4x 4 2.抛物线y =2x 2 ,y =-2x 2 ,y =12 x 2 的共同性质是( ) A.开口向上 B.对称轴是y 轴 C.都有最高点 随x 的增大而增大 3.若二次函数y =(x -m)2-1,当x≤1时,y 随x 的增大而减小,则m 的取值范围是( ) =1 >1 ≥1 ≤1 4.如图,AB 是⊙O 的直径.若∠BAC =35°,那么∠ADC =( ) ° ° ° ° 5.在同圆中,下列四个命题:①圆心角是顶点在圆心的角;②两个圆心角相等,它们所对的弦也相等;③两条弦相等,它们所对的弧也相等;④等弧所对的圆心角相等.其中真命题有( ) 个 个 个 个 6.如图,CD 是⊙O 的直径,弦AB ⊥CD 于E ,连接BC 、BD.下列结论错误的是( ) =BE B. =DE D. .∠DBC =90° 7.如图,AD 、AE 、CB 均为⊙O 的切线,D 、E 、F 分别是切点,AD =8,则△ABC 的周长为( ) D.不能确定 8.如果二次函数y =ax 2+bx +c 的图象如图所示,那么一次函数y =bx +c 和反比例函数y =b x 在同一坐标系中的图象大致是( ) 9.如图,圆形薄铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O ,三角尺的直角顶点C 落在直尺的10cm 处,铁片与直尺的唯一公共点A 落在直尺的14cm 处,铁片与三角尺的唯一公共点为B.下列说法错误的是( ) A.圆形铁片的半径是4cm B.四边形AOBC 为正方形 C.弧AB 的长度为4πcm D.扇形OAB 的面积是4πcm 2 10.已知二次函数y =ax 2+bx +c(a≠0)的图象如图所示,并且关于x 的一元二次方程ax 2+bx +c -m =0有两个不相等的实数根,下列结论:①b 2-4ac <0;②abc >0;③a -b +c <0;④m >-2,其中正确的个数有( ) 11.如图,扇形OAB 的圆心角为120°,半径为3,则该扇形的弧长为 (结果保留π). 二次函数 **测试试卷 考试范围:xxx ;考试时间:100分钟;命题人:xxx 姓名:__________班级:__________考号:__________ 注意事项: 1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上 一、单项选择 1. 设函数f(x)=ax 5+bx 3+cx +7(a ,b ,c 为常数,x ∈R),若f(-7)=-17,则f(7)=( ). A .31 B .17 C .-31 D .24 【答案】A 2. 已知一次函数y ax b =+的图象过第一、二、四象限,且与x 轴交于点(2,0),则关于x 的不等式(1)0a x b -->的解集为( ) A .x <-1 B .x >-1 C . x >1 D .x <1 【答案】A 3. 已知()f x 是定义在R 上的偶函数, 且在[0,)+∞上是增函数, 则一定有( ) A .423()(1)4f f a a ->++ B .3()4f -≥42(1)f a a ++ C .423()(1)4f f a a -<++ D .3 ()4 f -≤42(1)f a a ++ 【答案】C 4. 已知函数f(x)=21 1 x x -+,则f(x)( ) A .在(-∞,0)上单调递增 B .在(0,+∞)上单调递增 C .在(-∞,0)上单调递递 D .在(0,+∞)上单调递减 【答案】B 5. 函数3 ()ln f x x x =-的零点所在的大致区间是( ) A .(1,2) B .(2,3) C .(3,4) D .(3,)+∞ 【答案】B 6. 已知函数y =使函数值为5的x 的值是( ) A .-2或2 B .2或- C .-2 D .2或-2或- 【答案】C 7. 函数()f x =的定义域为 ( ) A .(-3,0] B .(-3,1] C .(,3)(3,0]-∞-- D .(,3)(3,1]-∞-- 【答案】A 8. 已知函数f(x)是定义在R 上的增函数,则函数y=f(|x-1|)-1的图象可能是 【答案】 B . 9. 下列说法中,不正确的是( ). A .图像关于原点成中心对称的函数一定是奇函数 B .奇函数的图像一定经过原点 C .偶函数的图像若不经过原点,则它与x 轴交点个数一定是偶数 D .图像关于y 轴对称的函数一定是偶函数 【答案】B 10. 函数1 ()ln (1)1 f x x x x =- >-的零点所在的区间为( ) A.3(1,)2 B.3(,2)2 C.5(2,)2 D.5 (,3) 2 【答案】C 11. 下列函数中,既是偶函数又在区间(0,+ ∞)上单调递减的是( ) A .1 y x = B .x y e -= C .21y x =-+ D .lg ||y x = 【答案】C 12. 抛物线3)2(2+-=x y 的顶点坐标是( ) A .(2,3) B .(–2,3) C .(2,–3) D .(–2,–3) 【答案】A 13. 函数f(x) 的定义域是( ). 二次函数 若()2 f x x bx c =++,且()10f =,()30f =,求()1f -的值. 变式1:若二次函数()2 f x ax bx c =++的图像的顶点坐标为()2,1-,与y 轴的交点坐标为(0,11), 则 A .1,4,11a b c ==-=- B .3,12,11a b c === C .3,6,11a b c ==-= D .3,12,11a b c ==-= 变式2:若()()2 23,[,]f x x b x x b c =-+++∈的图像x =1对称,则c =_______. 变式3:若二次函数()2 f x ax bx c =++的图像与x 轴有两个不同的交点()1,0A x 、()2,0B x ,且 2212269 x x += ,试问该二次函数的图像由()()2 31f x x =--的图像向上平移几个单位得到? 2. 将函数()2 361f x x x =--+配方,确定其对称轴,顶点坐标,求出它的单调区间及最大值或最小值, 并画出它的图像. 变式1:已知二次函数()2 f x ax bx c =++,如果()()12f x f x =(其中12x x ≠),则122x x f +?? = ??? A .2b a - B .b a - C . c D .244ac b a - 变式2:函数()2 f x x px q =++对任意的x 均有()()11f x f x +=-,那么()0f 、()1f -、() 1f 的大小关系是 A .()()()110f f f <-< B .()()()011f f f <-< C .()()()101f f f <<- D .()()()101f f f -<< 变式3:已知函数()2 f x ax bx c =++的图像如右图所示, 请至少写出三个与系数a 、b 、c 有关的正确命题_________. 3.单调性 x y O二次函数和圆综合(压轴题+例题+巩固+答案解析)
高考资料 二次函数基础练习题大全(含答案)
二次函数与圆结合的压轴题Word版
2021届新高考数学(文)复习小题必刷第05练 二次函数与幂函数(解析版)
-圆与二次函数综合题精练(带答案)教学文案
二次函数的实际应用题-中考数学题型专项练习
高中数学专题-二次函数综合问题例谈
二次函数与圆综合训练(含解析)
初中中招二次函数和圆的综合体包含答案
专题63 构造圆与隐形圆在二次函数中的综合问题(解析版)
完整word版,高考数学复习二次函数测试题
圆与二次函数综合练习
秒杀二次函数综合问题(高考专题)
中考专题:圆与二次函数结合题
初三数学中考专题复习二次函数和圆专题综合检测
二次函数高考练习题
二次函数经典练习题