
角平分线四大模型
模型1 角平分线的点向两边作垂线
如图,P是∠MON的平分线上一点,过点P作PA⊥OM于点A,PB⊥ON于点B,则PB=PA
模型分析
利用角平分线的性质:角平分线上的点到角两边的距离相等,构造模型,为边相等、角相等、三角形全等创造更多的条件,进而可以快速找到解题的突破口
模型实例
(1)如图①,在△ABC中,∠C=90°,AD平分∠CAB,BC=6,BD=4,那么点D到直线AB的距离是
解答:如图,过点D作DE⊥AB于点E,∵AD平分∠CAB,∴CD=DE.
∵CB=6,BD=4,∴DE=CD=2,即点D到直线AB的距离是2.
(2)如图②,∠1=∠2,∠3=∠4,求证:AP平分∠BAC
证明:如图,过点P作PD⊥AB于点D,PE⊥BC于点E,PF⊥AC于点F,
∵∠1=∠2,∴PD=PE,∵∠3=∠4, ∴PE=PF,∴PD=PF
又∵PD⊥AB,PF⊥AC,∴AP平分∠BAC(角平分线的判定)
练习
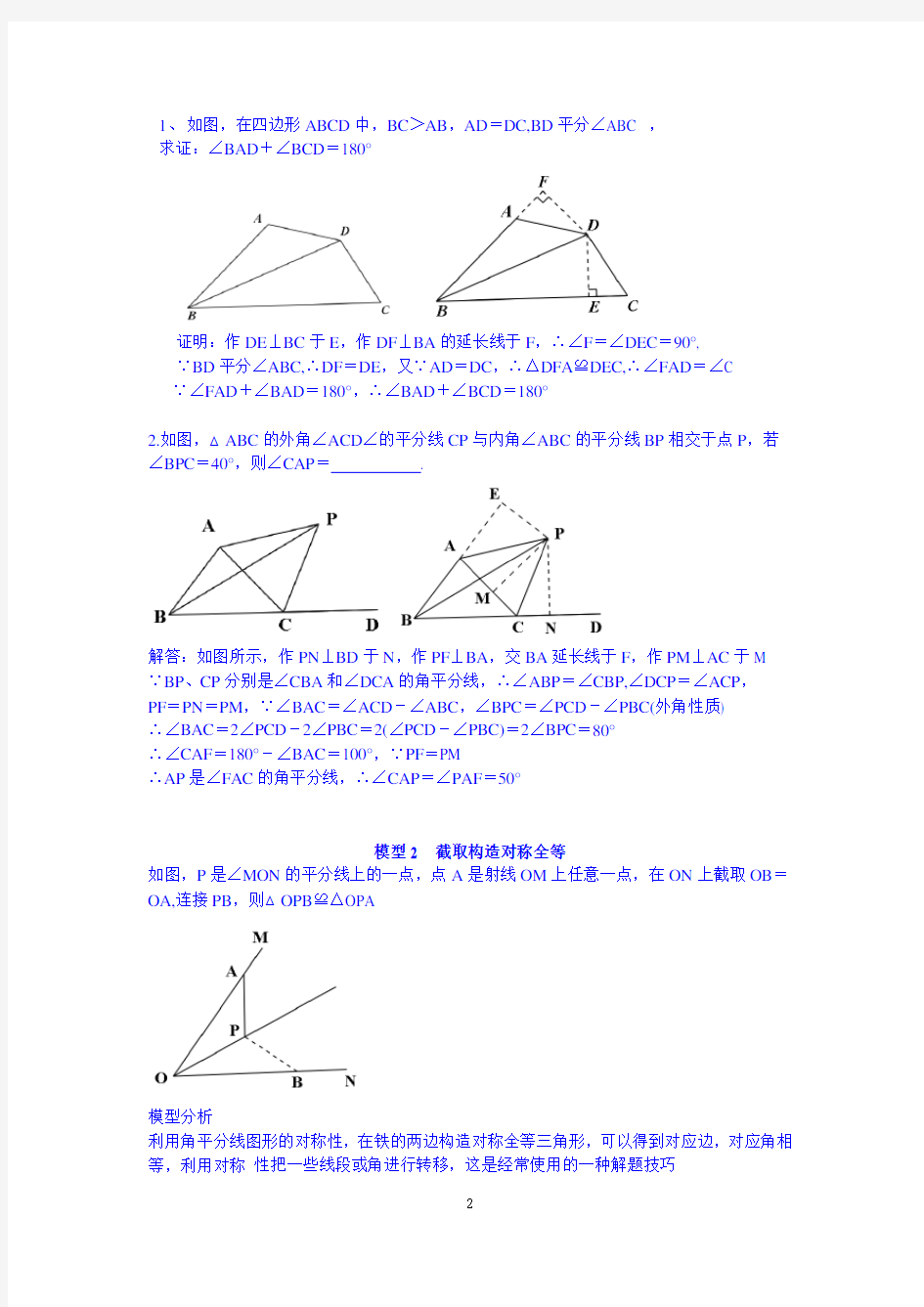
1、如图,在四边形ABCD中,BC>AB,AD=DC,BD平分∠ABC ,
求证:∠BAD+∠BCD=180°
证明:作DE⊥BC于E,作DF⊥BA的延长线于F,∴∠F=∠DEC=90°,
∵BD平分∠ABC,∴DF=DE,又∵AD=DC,∴△DFA≌DEC,∴∠FAD=∠C
∵∠FAD+∠BAD=180°,∴∠BAD+∠BCD=180°
2.如图,△ABC的外角∠ACD∠的平分线CP与内角∠ABC的平分线BP相交于点P,若∠BPC=40°,则∠CAP=.
解答:如图所示,作PN⊥BD于N,作PF⊥BA,交BA延长线于F,作PM⊥AC于M
∵BP、CP分别是∠CBA和∠DCA的角平分线,∴∠ABP=∠CBP,∠DCP=∠ACP,
PF=PN=PM,∵∠BAC=∠ACD-∠ABC,∠BPC=∠PCD-∠PBC(外角性质)
∴∠BAC=2∠PCD-2∠PBC=2(∠PCD-∠PBC)=2∠BPC=80°
∴∠CAF=180°-∠BAC=100°,∵PF=PM
∴AP是∠FAC的角平分线,∴∠CAP=∠PAF=50°
模型2 截取构造对称全等
如图,P是∠MON的平分线上的一点,点A是射线OM上任意一点,在ON上截取OB=OA,连接PB,则△OPB≌△OPA
模型分析
利用角平分线图形的对称性,在铁的两边构造对称全等三角形,可以得到对应边,对应角相等,利用对称性把一些线段或角进行转移,这是经常使用的一种解题技巧
模型实例
(1)如图①所示,在△ABC中,AD是△BAC的外角平分线,P是AD上异于点A的任意一点,试比较PB+PC与AB+AC的大小,并说明理由
解题:
PB+PC>AB+AC
证明:在BA的延长线上取点E, 使AE=AB,连接PE,∵AD平分∠CAE
∴∠CAD=∠EAD,在△AEP与△ACP中,∵AE=AB,∠CAD=∠EAD,
AP=AP,∴△AEP≌△ACP (SAS),∴PE=PC
∵在△PBE中:PB+PE>BE,BE=AB+AE=AB+AC,∴PB+PC>AB+AC
(2)如图②所示,AD是△ABC的内角平分线,其它条件不变,试比较PC-PB与AC-AB的大小,并说明理由
解答:AC-AB>PC-PB
证明:在△ABC中, 在AC上取一点E,使AE=AB ,∴AC-AE=AB-AC=BE
∵AD平分∠BAC ,∴∠EAP=∠BAP ,在△AEP和△ACP中
∴△AEP≌△ABP (SAS) ,∴PE=PB ,∵在△CPE中
CE>CP-PE ,∴AC-AB>PC-PB
练习
1.已知,在△ABC中,∠A=2∠B,CD是∠ACB的平分线,AC=16,AD=8,
求线段BC的长
解:如图在BC边上截取CE=AC,连结DE,在△ACD和△ECD中
?
?
?
?
?
=
∠
=
∠
=
CD
CD
ECD
ACD
EC
AC
∴△ACD ≌△ECD(SAS)
∴AD =DE , ∠A =∠1 ,∵∠A =2∠B ,∴∠1=2∠B ,
∵∠1=∠B +∠EDB , ∴∠B =∠EDB ,
∴EBB =ED , ∴EB =DA =8,BC =EC +BE =AC +DA =16+8=24
2. 在△ABC 中,AB =AC,∠A =108°,BD 平分∠ABC ,
求证:BC =AB +CD
证明:在BC 上截取BE =BA ,连结DE ,∵BD 平分∠ABC,BE =AB,BD =BD
∴△ABD ≌△EBD(SAS),∴∠DEB =∠A =108°,∴∠DEC =180°-108°=72°
∵AB =AC ,∴∠C =∠ABC
=1
2
(180°-108°)=36°,∴∠EDC =72° , ∴∠DEC =∠EDC ,∴CE =CD ,∴BE +CE =AB +CD ,∴BC =AB +CD
3.如图所示,在△ABC 中,∠A =100°,∠ABC =40°,BD 是∠ABC 的平分线,延长BD 至E ,使DE =AD ,求证:BC =AB +CE
证明:在CB 上取点F ,使得BF =AB,连结DF ,∵BD 平分∠ABC ,BD =BD
∴△ABD ≌△FBD ,∴DF =AD =DE,∠ADB =∠FDB ,∴BD 平分∠ABC
∴∠ABD =20°,则∠ADB =180°-20°-100°=60°=∠CDE
∠CDF =180°-∠ADB -∠FDB =60°,∴∠CDF =∠CDE ,在
△CDE 和△CDF 中 ??
???=∠=∠=CD CD CDE CDF DF DE
∴△CDE ≌CDF ,∴CE =CF ,∴BC =BF +FC =AB +CE
模型3 角平分线+垂线构造等腰三角形
如图,P 是∠MON 的平分线上一点,AP 丄OP 于P 点,延长AP 交ON 于点.B,则△AOB 是等腰三角形.
模型分析
构造此模型可以利用等腰三角形的"三线合一”,也可以得到两个全等的直角三角形.进而得到对应边.对应角相等.这个模型巧妙地把角平分线和三线合一联系了起来.
模型实例
如图.己知等腰直角三角形ABC 中,∠A=90°, AB=AC, BD 平分∠ABC, C£丄BD.垂足为E.求证:BD=2C£.
解答:如图,延长CE 、BA 交于点F,∵CE 丄BD 于E, ∠BAC=90°,∴∠BAD=∠CED. ∴∠ABD=∠ACF.又∵AB=AC, ∠BAD=∠CAF=90°, ∴△ABD ≌△ACF.∴ BD=CF. ∵BD 平分∠ABC, ∴∠CBE=∠FBE. 又BE=BE,∴△BCE ≌△BFE.
∴CE=EF. ∴BD=2CE.
练习
1.如图.在△ABC 中.BE 是角平分线.AD 丄BE.垂足为D.求证:∠2=∠1+∠C.
证明:延长AD 交BC 于F,∵AD ⊥BE, ∴∠ADB=∠BDF=90°, ∵∠ABD=∠FBD, ∴ ∠2=∠BFD. ∵∠BFD=∠1+∠C,∴∠2=∠1+∠C.
2.如图.在△ABC 中. ∠ABC=3∠C,AD 是∠BAC 的平分线, BE 丄AD 于点E.
求证:1()2
BE AC AB =-.
(2)证明:延长BE 交AC 于点F.∵AD 为∠BAC 的角平分线,∴∠BAD=∠CAD.∵AE=AE, ∴∠BAE=∠FAE,则△AEB ≌△AEF ,∴AB=AF, BE=EF, ∠ 2=∠3.∴AC-AB=AC-AF=FC. ∵∠ABC=3∠C,∴∠2+∠1=∠3+∠1=∠1+∠C+∠1=3∠C.∴2∠1=2∠C
即∠1=∠C ∴BF=FO=2BE.∴()1122
BE FC AC AB =
=-
模型4 角平分线+平行线
模型分析
有角平分线时.常过角平分线上一点作角的一边的平行线. 构造等腰三角形.为证明结论提供更多的条件.体现了用平分线与等腰三角形之间的密切关系.
模型实例
解答下列问题:
(1)如图①.△ABC中,EF∥BC,点D在EF上,BD、CD分别平分∠ABC、∠ACB.写出线段EF与BE、CF有什么数量关系?
(2)如图②,BD平分∠ABC,CD平分外角∠ACG. DE//BC交AB于点E,交AC于点F,线段EF与BE、CF有什么数量关系?并说明理由.
(3)如图③,BD、CD为外角∠CBM、∠BCN的平分线,DE//BC交AB延长线于点E.交AC 延长线于点F,直接写出线段EF与BE、CF有什么数关系?
解答:(1) ∵EF//BC,∴∠EDB=∠DBC.∴BD平分∠EBC,∴∠EBD=∠DBC=EDB. ∴EB=ED. 同理:DF=FC. ∴EF=ED+DF=BE+CF.
(2)图②中有EF=BE=CF,BD平分∠BAC,∴∠ABD=∠DBC.又DE//BC、∴∠EDB=∠DBC. ∴DE=EB.同理可证:CF=DF ∴EF=DE-DF=BE-CF.
(3) EF=BE+CF.
练习
1.如图. 在△ABC中,∠ABC和∠ACB的平分线交于点E.过点E作MN∥BC交AB于M点. 交AC于N点.若BM+CN=9,则线段MN的长为.
解答:∵∠ABC、∠ACB的平分线相交于点E,∴MBE=∠EBC,∠ECN=∠ECB.∵MN//BC, ∴∠EBC=∠MEB, ∠NEC=∠ECB. ∴∠MBE-∠MEB, ∠NEO=∠ECN.∴BM=ME, EN=CN. ∴MN=ME+EN,即MN=BM+CN.∵BM+CN=9,∴MN=9.
2. 如图. 在△ABC中,AD平分∠BAC.点E、F分別在BD,AD上,EF∥AB.且DE=CD,求证:EF=AC.
证明:如图,过点C作CM∥AB交AD的延长线于点M,∵AB∥EF,∴CM∥EF.∴∠3=∠4. ∵DE=CD, ∠5=∠6, ∴△DEF≌△DCM.∴EF=CM. ∵AB//CM,∴∠2=∠4. ∵∠1=∠2,
∴∠1=∠4.∴CM=AC.∴EF=AC
3.如图.梯形ABCD中,AD∥BC,点E在CD上,且AE平分∠BAD.BE平分∠ABC.求证:
AD=AB-BC.
证明:延长AD、BE交于点F.∵AD∥BC,∴∠2=∠F. ∵∠1=∠2,∴∠1=∠F.∴AB=AF.
∵AE平分∠BAD∴BE=EF. ∵∠DEF=∠CEB,
∴△DEF≌△CEB.∴DF=BC.∴AD=AF-DF=AB-BC.
中考常考几何模型 专题16 角平分线四大模型 1、角平分线上的点向两边作垂线 如图,P 是∠MON 的平分线上一点,过点 P 作 PA⊥OM 于点 A,PB⊥ON 于点 B。 结论:PB=PA。 2、截取构造对称全等 如图,P 是∠MON 的平分线上一点,点 A 是射线 OM 上任意一点,在 ON上截取 OB=OA,连接 PB。结论:△OPB≌△OPA。 3、角平分线+垂线构造等腰三角形 如图,P 是∠MO 的平分线上一点,AP⊥OP 于 P 点,延长 AP 于点 B。 结论:△AOB 是等腰三角形。 4、角平分线+平行线 如图,P 是∠MO 的平分线上一点,过点 P 作 PQ∥ON,交 OM 于点 Q。结论:△POQ 是等腰三角形。
模型精练: 1.(2019?东平县二模)如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,若∠BPC=40°,则∠CAP=() A.40°B.45°C.50°D.60° 【点睛】根据外角与内角性质得出∠BAC的度数,再利用角平分线的性质以及直角三角形全等的判定,得出∠CAP=∠F AP,即可得出答案 【解析】解:延长BA,作PN⊥BD,PF⊥BA,PM⊥AC, 设∠PCD=x°, ∵CP平分∠ACD, ∴∠ACP=∠PCD=x°,PM=PN, ∵BP平分∠ABC, ∴∠ABP=∠PBC,PF=PN,
∴PF=PM, ∵∠BPC=40°, ∴∠ABP=∠PBC=∠PCD﹣∠BPC=(x﹣40)°, ∴∠BAC=∠ACD﹣∠ABC=2x°﹣(x°﹣40°)﹣(x°﹣40°)=80°, ∴∠CAF=100°, 在Rt△PF A和Rt△PMA中, {PA=PA PM=PF, ∴Rt△PF A≌Rt△PMA(HL), ∴∠F AP=∠P AC=50°. 故选:C. 2.(2019?桂平市期末)如图,在△ABC中,∠C=90°,AD平分∠CAB,BC=12cm,BD=8cm,那么点D到直线AB的距离是() A.2cm B.4cm C.6cm D.10cm 【点睛】先求出CD的长,过点D作DE⊥AB于点E,根据角平分线上的点到角的两边的距离相等的性质可得DE=CD,从而得解. 【解析】解:如图,过点D作DE⊥AB于点E,
几何证明——角平分线模型(高级) 【经典例题】 例1、已知如图,ABC ?中,BC AC =,AD 平分CAB ∠,若ο 100=∠C ,求证:CD AD AB +=。 例2、如图,已知在ABC ?中,ο 60=∠B ,ABC ?的角平分线CE AD ,相交于点O ,求证:AC CD AE =+。 E O B 例3、如图,BD 平分ABC ∠,?=∠45ADB ,BC AE ⊥,求AED ∠. A B C D 例4、已知,如图ABC ?中,AD 为ABC ?的角平分线,求证:BD AC DC AB ?=?.
例5、如图,已知P 为锐角△ABC 内一点,过P 分别作AB AC BC ,,的垂线,垂足分别为F E D ,,,BM 为ABC ∠的平分线,MP 的延长线交AB 于点N ;如果PF PE PD +=,求证:CN 是ACB ∠的平分线。 A B C N M P D E F 例6、如图,在梯形ABCD 中,BC AD //,DC AB =,?=∠80ABC ,E 是腰CD 上一点,连接BE 、AC 、 AE ,若?=∠60ACB ,?=∠50EBC ,求EAC ∠的度数. B C E 例7、已知:ABC ?中,BC AB <,AC 的中点为M ,AC MN ⊥交ABC ∠的角平分线于N . (1)如图1,若?=∠60ABC ,求证:BN BC BA 3= +;
(2)如图2,若?=∠120ABC ,则BA 、BC 、BN 之间满足什么关系式,并对你得出的结论给予证明. A C 【提升训练】 1、在ABC ?中,AB AC >,AD 是BAC ∠的平分线.P 是AD 上任意一点.求证:AB AC PB PC ->-. B 2、如图,在ABC ?中,A ∠等于ο 60,BE 平分CD ABC ,∠平分ACB ∠,求证:EH DH =。 3、如图所示,在ABC ?中,AD 平分BAC ∠,AD AB =,CM AD ⊥于M ,求证:2AB AC AM +=。
初中几何常见模型解析 模型一:手拉手模型-旋转型全等 (1)等边三角形 ?条件:均为等边三角形 ?结论:①;②;③平分。(2)等腰 ?条件:均为等腰直角三角形 ?结论:①;②; ?③平分。 (3)任意等腰三角形 ?条件:均为等腰三角形 ?结论:①;②; ?③平分 模型二:手拉手模型-旋转型相似 (1)一般情况 ?条件:,将旋转至右图位置 ?结论: ?右图中①; ?②延长AC交BD于点E,必有
(2)特殊情况 ?条件:,,将旋转至右图位置 ?结论:右图中①;②延长AC交BD于点E,必有;③; ④; ⑤连接AD、BC,必有; ⑥(对角线互相垂直的四边形)
模型三:对角互补模型 (1)全等型-90° ?条件:①;②OC平分 ?结论:①CD=CE; ②;③ ?证明提示: ①作垂直,如图,证明; ②过点C作,如上图(右),证明; ?当的一边交AO的延长线于点D时: 以上三个结论:①CD=CE(不变); ②;③ 此结论证明方法与前一种情况一致,可自行尝试。 (2)全等型-120° ?条件:①; ?②平分; ?结论:①;②; ?③ ?证明提示:①可参考“全等型-90°”证法一; ②如图:在OB上取一点F,使OF=OC,证明为等边三角形。(3)全等型-任意角 ?条件:①;②; ?结论:①平分;②; ?③.
?当的一边交AO的延长线于点D时(如右上图): 原结论变成:①;②; ③; 可参考上述第②种方法进行证明。请思考初始条件的变化对模型的影响。 ?对角互补模型总结: ①常见初始条件:四边形对角互补;注意两点:四点共圆及直角三角形斜边中线; ②初始条件“角平分线”与“两边相等”的区别; ③两种常见的辅助线作法; ④注意平分时,相等如何推导?
每日一题:三角形中角平分线的基本模型 武穴市百汇学校徐国纲 在初中阶段,角平分线问题涉及角度的计算和证明。经过总结归纳,有相当部分可以转化为基本模型,掌握这些模型,可以为我们迅速找到解题思路,形成良好的数学思维习惯奠定基础。下面举例说明。 【模型一】角平分线+垂直一边 若PA⊥OM于点A,如图a,可以过P点作PB⊥ON于点B,则PB=PA。可记为“图中有角平分线,可向两边作垂线”,显然这个基本图形中可以利用角平分线的性质定理,也可以得到一组全等三角形; 【模型二】角平分线+斜线 若点A是射线OM上任意一点,如图b,可以在ON上截取OB=OA,连接PB,构造△OPB≌△OPA。可记为“图中有角平分线,可以将图形对折看,对称以后关系现”。 【模型三】角平分线+垂线 若AP⊥OP于点P,如图c,可延长AP交ON于点B,构造△AOB是等腰三角形,P是底边AB 的中点,可记为“角平分线加垂线,三线合一试试看”,实际上这是“两线合一”的一种情形,这个图形中隐含着全等和等腰三角形; 【模型四】角平分线+平行线 若过P点作PQ∥ON交OM于点Q,如图d,可以构造△POQ是等腰三角形,可记为“角平分线+平行线,等腰三角形必呈现”,这个基本图形使用频率那是相当的高,切记。 【模型五】角平分线+对角互补 若∠A+∠C=180°,BD是∠ABC的平分线,则AD=CD. 【模型六】夹角模型 ①BP、CP分别是∠ABC、∠ACE的角平分线,则:∠P=90°+1 2 ∠A. ②BP、CP分别是∠ABC、∠ACE的角平分线,则:∠P=1 2 ∠A.
BP、CP分别是∠CBD、∠BCD的角平分线,则:∠D=90°-1 2 ∠B.
角平分线四大模型 模型一: 这个模型的基本思想是过角平分线上一点P 作角两边的垂线。如图中PA ⊥OA ,PB ⊥OB 。容易通过全等得到PA=PB (角平分线性质)。 注意:题目一般只有一条垂线,需要自行补出另一条垂线。甚至只给你一条角平分线,自行添加两条垂线。 例题1:AF 是△ABC 的角平分线。P 是AF 上任意一点。过点P 作AB 平行线交BC 于点D ,作AC 的平行线交BC 与点E 。证明:点F 到DP 的距离与点F 到EP 的距离相等。 拓展,如果点P 在AF 延长线上,结论是否依然成立? 例题2:如图正方形ABCD 的边长为4,∠DAC 的平分线交DC 于点E ,若点P 、Q 分别是AD 和AE 上的动点,则DQ+PQ 的最小值是__2√2__ E
模型二: 这个模型的基础是,在角平分线上任意找一点P ,过点P 作角平分线的垂线交角的两条边与A 、B 。这样就构造出了一个等腰三角形AOB ,即OA=OB 。这个模型还可以得到P 是AB 中点。 注意:这个模型与一之间的区别在于垂直 的位置。并且辅助线的添加方法一般是延长一段与角平分线垂直的线段。如图中的PB 。 例题1:如图,∠BAD=∠CAD ,AB>AC ,CD 垂直AD 于点D ,H 是BC 的中点。 求证:DH=1/2(AB-AC ) 提示:要使用到三角形中位线的性质,即三角形中位线是对应边的一半。 模型三: 这个模型的基础是在角的两边分别截取OA=OB ,然后在对角线上取任意一点P ,连接AP ,BP 。容易证得△APO ≌△BPO 。 注意:一般这样的模型最容易被孩子忽略,因为这个模型里没有的角度,因而对于孩子而言添出PB 这条辅助线是有难度的。添加这条辅助线的基本思想是在ON 上截 取OB ,使得AP=BP 。从而构造出一个轴对称。这样的模型一般会出现在截长补短里。 B B N
支付宝首页搜索“ 933314”领红包,每 天都能领。付款前记得用红包 第二讲角平分线模型的构造 3月 角平分线 (l)定义:如图2-1,如果∠AOB =∠BOC ,那么∠AOC=2∠AOB=2∠BOC ,像OB 这样,从一个角的顶点出发,把这个角分成相等的两个角的射线,叫作这个角的角平分线. (2)角平分线的性质定理 ①如果一条射线是一个角的平分线,那么它把这个角分成两个相等的角, ②在角的平分线上的点到这个角的两边的距离相等. (3)角平分线的判定定理 ①在角的内部,如果一条射线的端点与角的顶点重合,且把一个角分成两个等角,那么这条射线是这个角的平分线, ②在角的内部,到一个角两边距离相等的点在这个角的平分线上, 与角平分线有关的常用辅助线作法,即角平分线的四大基本模型, 已知P 是∠MON 平分线上一点, (l)若PA ⊥OM 于点A ,如图2-2(a),可以过P 点作PB ⊥ON 于点B ,则PB=PA.可记为“图中有角平分线,可向两边作垂线”. (a) O (b) (2)若点A 是射线OM 上任意一点,如图2-2(b),可以在ON 上截取OB=OA ,连接PB ,构造△OPB ∽△OPA.可记为“图中有角平分线,可以将图对 折看,对称以后关系现”. (3)若AP ⊥OP 于点P ,如图2-2(c),可以延长AP 交ON 于点B ,构造△AOB 是等腰三角形,P 是底边AB 的中点,可记为“角平分线加垂线,三线合一试试看”. (c) O (d) O (4)若过P 点作PQ ∥ON 交OM 于点Q ,如图2-2(d),可以构造△POQ 是等腰三角形,可记为“角平分线十平行线,等腰三角形必呈现”. 例1 (1)如图2-3(a),在△ABC 中,∠C=90。,AD 平分∠CAB ,BC=6cm ,BD=4cm ,那么点D 到直线AB 的距离是( )cm. 图2-3 (a ) (2)如图2-3(b),已知:∠1=∠2,∠3=∠4, 求证:AP 平分∠BAC . 图2-3(b )
角平分线四大模型 模型1 角平分线上的点向两边作垂线 如图,P 是∠MON 的平分线上一点,过点P 作PA ⊥OM 于点A ,PB ⊥ON 于点B 。 结论:PB=PA 。 模型分析 利用角平分线的性质:角平分线上的点到角两边的距离相等,构造模型,为边相等、角相等、三角形全等创造更多的条件,进而可以快速找到解题的突破口。 模型实例 (1)如图①,在△ABC 中,∠C=90°,AD 平分∠CAB ,BC=6,BD=4,那么点D 到直线AB 的距离是 ; (2)如图②,∠1=∠2,+∠3=∠4。 求证:AP 平分∠BAC 。 热搜精练 1.如图,在四边形ABCD 中,BC>AB ,AD=DC ,BD 平分∠ABC 。 求证:∠BAD+∠BCD=180°。 2.如图,△ABC 的外角∠ACD 的平分线CP 与内角∠ABC 的平分线BP 交于点 P ,若∠BPC=40°,则∠CAP= 。 N M O A B P 2图4321A C P B D A B C 图1A B D C
模型2 截取构造对称全等 如图,P 是∠MON 的平分线上一点,点A 是射线OM 上任意一点,在ON 上截取OB=OA ,连接PB 。 结论:△OPB ≌△OPA 。 模型分析 利用角平分线图形的对称性,在角的两边构造对称全等三角形,可以得到对应边、对应角相等。利用对称性把一些线段或角进行转移,这是经常使用的一种解题技巧。 模型实例 (1)如图①所示,在△ABC 中,AD 是△ABC 的外角平分线,P 是AD 上异于点 A 的任意一点,试比较PB+PC 与AB+AC 的大小,并说明理由; (2)如图②所示, AD 是△ABC 的内角平分线,其他条件不变,试比较 PC-PB 与AC-AB 的大小,并说明理由。 热搜精练 1.已知,在△ABC 中,∠A=2∠B ,CD 是∠ACB 的平分线,AC=16,AD=8。 求线段BC 的长。 A B D C P P O N M B A 图2D P A B C D C 1图P B A A B C D
中点模型 【模型1】倍长 1、倍长中线; 2、倍长类中线; 3、中点遇平行线延长相交 A B C D E A B C D E F E D C B A 【模型2】遇多个中点,构造中位线 1、直接连接中点; 2、连对角线取中点再相连 G A B C D E F A B C D E 【例1】在菱形ABCD 和正三角形BEF 中,∠ABC =60°,G 是DF 的中点,连接GC 、GE . (1)如图1,当点E 在BC 边上时,若AB =10,BF =4,求GE 的长; (2)如图2,当点F 在AB 的延长线上时,线段GE 、GC 有怎样的数量和位置关系,写出你的猜想,并给予证明; (3)如图3,当点F 在CB 的延长线上时,(2)问中的关系还成立吗?写出你的猜想,并给予证明. 图3 图2图1 A C D E F G D E F G C D E G A B B F C B A 【解答】 (1)延长EG 交CD 于点H 易证明△CHG ≌△CEG ,则GE = 注意G 的两端点D 、E 所在的直线DC ∥FE
F A (2)延长CG 交AB 于点I , 易证明△BCE ≌△FIE ,则△CEI 是等边三角形,GE =3GC ,且GE ⊥GC A F (3) E J 【例2】如图,在菱形ABCD 中,点E 、F 分别是BC 、CD 上一点,连接DE 、EF ,且AE =AF ,∠DAE =∠BAF . (1)求证:CE =CF ; (2)若∠ABC =120°,点G 是线段AF 的中点,连接DG 、EG ,求证:DG ⊥EG . G F E D C B A 【解答】 (1)证明△ABE ≌△ADF 即可; (2)延长DG 与AB 相交于点H ,连接HE ,证明△HBE ≌△EFD 即可 为什么是证明△BCE ≌△FIE 你理解吗? 你能写出解题思路和过程吗? 类似的为什么要延长CG 呢,可以延长EG 吗?
角平分线四大模型 模型1 角平分线的点向两边作垂线 如图,P是∠MON的平分线上一点,过点P作PA⊥OM于点A,PB⊥ON于点B,则PB=PA 模型分析 利用角平分线的性质:角平分线上的点到角两边的距离相等,构造模型,为边相等、角相等、三角形全等创造更多的条件,进而可以快速找到解题的突破口 模型实例 (1)如图①,在△ABC中,∠C=90°,AD平分∠CAB,BC=6,BD=4,那么点D到直线AB的距离是 解答:如图,过点D作DE⊥AB于点E,∵AD平分∠CAB,∴CD=DE. ∵CB=6,BD=4,∴DE=CD=2,即点D到直线AB的距离是2. (2)如图②,∠1=∠2,∠3=∠4,求证:AP平分∠BAC 证明:如图,过点P作PD⊥AB于点D,PE⊥BC于点E,PF⊥AC于点F, ∵∠1=∠2,∴PD=PE,∵∠3=∠4, ∴PE=PF,∴PD=PF 又∵PD⊥AB,PF⊥AC,∴AP平分∠BAC(角平分线的判定) 练习 1、如图,在四边形ABCD中,BC>AB,AD=DC,BD平分∠ABC , 求证:∠BAD+∠BCD=180°
证明:作DE⊥BC于E,作DF⊥BA的延长线于F,∴∠F=∠DEC=90°, ∵BD平分∠ABC,∴DF=DE,又∵AD=DC,∴△DFA≌DEC,∴∠FAD=∠C ∵∠FAD+∠BAD=180°,∴∠BAD+∠BCD=180° 2.如图,△ABC的外角∠ACD∠的平分线CP与内角∠ABC的平分线BP相交于点P,若∠BPC=40°,则∠CAP = . 解答:如图所示,作PN⊥BD于N,作PF⊥BA,交BA延长线于F,作PM⊥AC于M ∵BP、CP分别是∠CBA和∠DCA的角平分线,∴∠ABP=∠CBP,∠DCP=∠ACP, PF=PN=PM,∵∠BAC=∠ACD-∠ABC,∠BPC=∠PCD-∠PBC(外角性质) ∴∠BAC=2∠PCD-2∠PBC=2(∠PCD-∠PBC)=2∠BPC=80° ∴∠CAF=180°-∠BAC=100°,∵PF=PM ∴AP是∠FAC的角平分线,∴∠CAP=∠PAF=50° 模型2 截取构造对称全等 如图,P是∠MON的平分线上的一点,点A是射线OM上任意一点,在ON上截取OB=OA,连接PB,则△OPB ≌△OPA
B B B D A B C 几何证明——角平分线模型(中级) 【知识要点】 1、角平分线: (1)角平分线性质定理:角平分线上的点到这个角的两边的距离相等(作用:证明两条线段相等); (2)逆定理:在角的内部,到角的两边距离相等的点在这个角的角平分线上。(作用:证明两角相等或一 条射线是一个角的角平分线)。 2、角平分线常见用法(或辅助线作法): ①垂两边:如图1,已知BP 平分ABC ∠,过点P 作PA AB ⊥,PC BC ⊥,则PA PC =。 ②截两边:如图2,已知BP 平分MBN ∠,点A BM 上,在BN 上截取BC BA =,则ABP ?≌CBP ?。 ③角平分线+平行线→等腰三角形: 如图3,已知BP 平分ABC ∠,//PA AC ,则AB AP =; 如图4,已知BP 平分ABC ∠,//EF PB ,则BE BF =。 (1) (2) (3) (4) ④三线合一(利用角平分线+垂线→等腰三角形): 如图5,已知AD 平分BAC ∠,且AD BC ⊥,则AB AC =,BD CD =。 (5) 3、角平分线比例定理 如图6,AD 为ABC ?的角平分线,则 AB BD AC CD =或AB AC BD CD = 。 (6) 【经典例题】 例1、已知如图,ABC ?中,BC AC =,AD 平分CAB ∠,若ο 90=∠C ,求证:CD AC AB +=; C
例2、如图,在ABC Rt ?中,ο 90=∠ACB ,AB CD ⊥于D ,AF 平分CAB ∠交CD 于E ,交CB 于F , 且AB EG //交CB 于G 。试求:CF 与GB 的大小关系如何? E C A B D F G 例3、已知如图,ABC ?中,BC AC =,AD 平分CAB ∠,若ο 108=∠C ,求证:BD AC AB +=; 例4、如图:已知I 是ABC ?的内心,//DI AB 交BC 于点D ,//EI AC 交BC 于E 。求证:DIE ?的周长等于BC 。 A B C I D E 例5、如图:已知在ABC ?中,ABC ∠的平分线与ACB ∠的外角平分线交于点D ,DE ∥BC ,交AB 于点E ,交AC 于点F ,求证:FC BE EF -=。
一、等积变换模型 ⑴等底等高的两个三角形面积相等; 其它常见的面积相等的情况 ⑵两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比。 如上图12::S S a b = ⑶夹在一组平行线之间的等积变形,如下图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD 。 ⑷正方形的面积等于对角线长度平方的一半; ⑸三角形面积等于与它等底等高的平行四边形面积的一半; 二、鸟头定理(共角定理)模型 两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。 如图,在ABC △中,,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上, 五大模型
E 在AC 上(如图2),则:():()ABC ADE S S AB AC AD AE =??△△ 图1 图2 三、蝴蝶定理模型 任意四边形中的比例关系(“蝴蝶定理”): ①1243::S S S S =或者1324S S S S ?=?②()()1243::AO OC S S S S =++ 蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。 梯形中比例关系(“梯形蝴蝶定理”) ①2213::S S a b = ②221324::::::S S S S a b ab ab =; ③梯形S 的对应份数为()2a b +。 四、相似模型 相似三角形性质: 金字塔模型 沙漏模型
角平分线四大模型 模型一:角平分线上的点向两边作垂线 如图,P是∠MON的平分线上一点,过点P作PA⊥OM于点A,PB⊥ON于点 B,则PB=PA. 模型分析:利用角平分线的性质:角平分线上的点到角两边的距离相等,构造模型,为边相等、角相等、三角形全等创造更多的条件,进而可以快速找到解题的突破口。 例1:(1)如图①,在△ABC,∠C=90°,AD平分∠CAB,BC=6cm,BD=4cm,那么点D到AB的距离是___cm (2)如图②,已知∠1=∠2,∠3=∠4,求证:AP平分∠BAC. 练习1 如图,在四边形ABCD中,BC>BA,AD=DC,BD平分∠ABC. 求证:∠BAD+∠C=180° 练习2 如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,若∠BPC=40°,则∠CAP=()
模型二:截取构造对称全等 如图,P是∠MON的平分线上一点,点A是射线OM上任意一点,在ON上 截取OB=OA,连接PB,则△OPB△OPA. 模型分析:利用角平分线图形的对称性,在角的两边构造对称全等三角形,可以得到对应边、对应角相等、利用对称性把一些线段或角进行转移,这是经常使用的一种解题技巧。 例2:(1)如图①所示,在△ABC中,AD是△BAC的外角平分线,P是AD上异于点A的任意一点,试比较PB+PC与AB+AC的大小,并说明理由. (2)如图②所示.AD是△ABC的内角平分线,其他条件不变,试比较PC -PB与AC-AB的大小,并说明理由. 练习 3 已知:△ABC中,∠A=2∠B,CD是∠ACB的平分线,AC=16,AD=8,求线段BC的长。 练习4 已知,如图AB=AC,∠A=108°,BD平分∠ABC交AC于D,求证:BC=AB+CD. 练习5 如图,在△ABC中,∠A=100°,∠ABC=40°,BD是∠ABC的平分线,延长BD至E,使DE=AD.求证:BC=AB+CE.
1 一、角平分线的三种“模型” 模型一:角平分线+平行线→等腰三角形 如图1,过∠AOB 平分线OC 上的一点P ,作PE ∥OB ,交OA 于点E ,则EO=EP. A A A E P C E C D F E P O B B C O F B 图1 图2 图3 例1 如图2,∠ABC ,∠ACB 的平分线相交于点F ,过F 作DE ∥BC ,交AB 于点D ,交AC 于点E.求证:BD+EC=DE. 模型二:角平分线+垂线→等腰三角形 如图3,过∠AOB 平分线OC 上的一点P ,作EF ⊥OC ,交OA 于点E ,交OB 于点F ,则OE=OF ,PE=PF. 例2 如图4,BD 是∠ABC 的平分线,AD ⊥BD ,垂足为D ,求证:∠BAD=∠DAC+∠C. 模型三:角平分线+翻折→全等三角形 在△ABC 中,AD 是∠BAC 的平分线,沿角平分线AD 将△ABD 往右边折叠就得到如图5的图形.此时有:△ABD ≌△AB /D.此翻折 相当于在三角形的一边截取线段等于另一边,或延长一边等于另一边构造出相等的线段.用此方法可解决一些不相等的线段和差类问题. D A E A P / B C D B / B C 图5 图6 例3 如图6,点P 是△ABC 的外角∠CAD 的平分线上的一点.求证: PB+PC>AB+AC. 二、角平分线定理使用中的几种辅助线作法 一、已知角平分线,构造三角形 1、如图所示,在△ABC 中,∠ABC=3∠C ,AD 是∠BAC 的平分线,BE ⊥AD 于F 。 求证:1 ()2 BE AC AB =- 2、在△ABC 中,AD 平分∠BAC ,CE ⊥AD 于E .求证:∠ACE=∠B+∠ECD . 2 1F E D C B A A B D C E F 图
角平分线+平行应用模型的构造 一、近几年中考题往往由平行线,角平分线来推证同一三角形两个角相等,从而推证两边相等。或者由其中两个条件推证另一个条件 已知:如图7-9,在ΔABC中,CE是角平分线,EG∥BC,交AC边于F,交∠ACB的外角(∠ACD)的平分线于G,探究线段EF与FG的数量关系并证明你的结论. 1、如图,AC和BD相交于O,且AB∥DC,OA=OB, 求证:OC=OD. O D C B A 2.如图,△ABC中,AM,CM分别是角平分线,过M作DE∥AC 求证:AD+CE=DE 3.如图,∠AOB=30°,OC平分∠AOB,CD⊥OA于D,CE∥AO交OB于E CE=20cm,求CD的长。 4.如图,△ABC中,∠A=36°,AB=AC,BD平分∠ABC,DE∥BC, 5.则图中等腰三角形的个数() (A)1个(B)3个(C)4个(D)5个 A E B C D 第16题
E F C B A D 5如右图:∠DAE=∠ADE=15°,DE∥AB,DF⊥AB,若AE=8,则DF 等于( ) A.5 B.4 C . 3 D .2 6、如图,四边形ABCD 中,AD∥BC ,∠ABD =30o ,AB=AD ,DC ⊥BC 于点C ,若BD =2,求CD 的长。 二 由平行线想到全等三角形和等腰三角形。 例. 如图,已知,EG ∥AF ,请你从下面三个条件中,再选出两个作为已知条件,另一个作为结论,推出一个正确的命题。并证明这个命题(只写出一种情况)①AB=AC ②DE=DF ③BE=CF 已知:EG ∥AF,_______,_________. 求证:___________. 证明: G F E D C B A 1、已知:如图,△ABC 中,AB=AC ,D 点在AB 上,E 点在AC 的延长线上,且BD=CE ,连接DE ,交BC 于F.求证:DF=EF. C 第6题 F E C D B A
角平分线的几种辅助线 作法与三种模型 Company Document number:WUUT-WUUY-WBBGB-BWYTT-1982GT
一、角平分线的三种“模型” 模型一:角平分线+平行线→等腰三角形 如图1,过∠AOB平分线OC上的一点P,作PE∥OB,交OA于点E,则EO=EP. AAA EPCEC DFEP OBBCOFB 图1图2图3 例1如图2,∠ABC,∠ACB的平分线相交于点F,过F作DE∥BC,交AB于点D,交AC于点E.求证:BD+EC=DE. 模型二:角平分线+垂线→等腰三角形 如图3,过∠AOB平分线OC上的一点P,作 EF⊥OC,交OA于点E,交OB于点F,则OE=OF, PE=PF. 例2如图4,BD是∠ABC的平分线,AD⊥BD, 垂足为D,求证:∠BAD=∠DAC+∠C. 模型三:角平分线+翻折→全等三角形 在△ABC中,AD是∠BAC的平分线,沿角平分线AD将△ABD往右边折叠就得到如图5的图形.此时有:△ABD≌△AB/D.此翻折相当于在三角形的一边截取线段等于另一边,或延长一边等于另一边构造出相等的线段.用此方法可解决一些不相等的线段和差类问题. D AE AP /BC DB/BC
图5图6 例3 如图6,点P 是△ABC 的外角∠CAD 的平分线上的一点.求证:PB+PC>AB+AC. 二、角平分线定理使用中的几种辅助线作法 一、已知角平分线,构造三角形 1、如图所示,在△ABC 中,∠ABC=3∠C ,AD 是∠BAC 的平分线,BE ⊥AD 于F 。 求证:1 ()2 BE AC AB =- 2、在△ABC 中,AD 平分∠BAC ,CE ⊥AD 于E .求证:∠ACE=∠B+∠ ECD . 二、已知一个点到角的一边的距离,过这个点作另一边的垂线段 1、如图所示,∠1=∠2,P 为BN 上的一点,并且PD ⊥BC 于D ,AB +BC=2BD 。 求证:∠BAP +∠BCP=180°。 三、已知角平分线和其上面的一点,过这一点作角的两边的垂线段 1、如图所示,在△ABC 中,PB 、PC 分别是∠ABC 的外角的平分线,求证:∠1=∠2 2、2、如图2,AB ∥CD ,E 为AD 上一点,且BE 、CE 分别平分∠ABC 、∠BCD . 2 1F E D C B A N P E D C B A 2 1 P F E C B A A G C H D E F 图2 A B D C E F 图
N M O A B P 2图4 321A C P B D A B C 图1A B D C A B D C P 第二章 角平分线四大模型 模型1 角平分线上的点向两边作垂线 如图,P 是∠MON 的平分线上一点,过点P 作 PA ⊥OM 于点A ,PB ⊥ON 于点B 。 结论:PB=PA 。 模型分析 利用角平分线的性质:角平分线上的点到角两边的距离相等,构造模型,为边相等、角相等、三角形全等创造更多的条件,进而可以快速找到解题的突破口。 模型实例 (1)如图①,在△ABC 中,∠C=90°,AD 平分∠CAB ,BC=6,BD=4,那么点D 到直线AB 的距离是 ; (2)如图②,∠1=∠2,+∠3=∠4。 求证:AP 平分∠BAC 。 热搜精练 1.如图,在四边形ABCD 中,BC>AB ,AD=DC ,BD 平分∠ABC 。 求证:∠BAD+∠BCD=180°。 2.如图,△ABC 的外角∠ACD 的平分线CP 与内角∠ABC 的平分线BP 交于点 P ,若∠BPC=40°,则∠CAP= 。
P O N M B A 图2D P A B C D C 1图P B A A B C D A B C D E D C B A 模型2 截取构造对称全等 如图,P 是∠MON 的平分线上一点,点A 是射线OM 上任意一点,在ON 上截取OB=OA ,连接PB 。 结论:△OPB ≌△OPA 。 模型分析 利用角平分线图形的对称性,在角的两边构造对称全等三角形,可以得到对应边、对应角相等。利用对称性把一些线段或角进行转移,这是经常使用的一种解题技巧。 模型实例 (1)如图①所示,在△ABC 中,AD 是△ABC 的外角平分线,P 是AD 上异于点 A 的任意一点,试比较PB+PC 与AB+AC 的大小,并说明理由; (2)如图②所示, AD 是△ABC 的内角平分线,其他条件不变,试比较 PC-PB 与AC-AB 的大小,并说明理由。 热搜精练 1.已知,在△ABC 中,∠A=2∠B ,CD 是∠ACB 的平分线,AC=16,AD=8。 求线段BC 的长。 2.已知,在△ABC 中,AB=AC ,∠A=108°,BD 平分∠ABC 。 求证:BC=AB+CD 。 3.如图所示,在△ABC 中,∠A=100°,∠A=40°,BD 是∠ABC 的平分线,延 长BD 至E ,DE=AD 。求证:BC=AB+CE 。
B B E C B A 巧借三角形的两条内(外)角平分线夹角的模型解决问题 新北实验中学 严云霞 【基本模型】 三角形的两个内(外)角平分线所夹的角与第三个角之间的数量关系 模型一:当这两个角为内角时:这个夹角等于90°与第三个角一半的和(如图1); 模型二:当这两个角为外角时:这个夹角等于90°与第三个角一半的差(如图2); 模型三:当这两个角为一内角、一外角时:这个夹角等于第三个角一半(如图3); 【分析】三个结论的证明 例1、 如图1,△ABC 中,BD 、CD 为两个内角平分线, 试说明:∠D=90°+2 1 ∠A 。 (方法一)解:∵BD 、CD 为角平分线 ∴∠CBD =21∠ABC , ∠BCD =2 1 ∠ACB 。 在△BCD 中:∠D =180°-(∠CBD +∠BCD ) =180°-21 (∠ABC +∠ACB ) =180°-21 (180°-∠A ) =180°-21×180°+21 ∠A =90°+2 1 ∠A (方法二)解:连接AD 并延长交BC 于点E 解:∵BD 、CD 为角平分线 ∴∠CBD =21∠ABC , ∠BCD =2 1 ∠ACB 。 ∵∠BDE 是△ABD 的外角 ∴∠BDE =∠BAD+∠ABD =∠BAD+2 1 ∠ABC
同理可得∠CDE =∠CAD+2 1 ∠ACB 又∵∠BDC =∠BDE+∠CDE ∴∠BDC =∠BAD+21∠ABC+∠CAD+21 ∠ACB =∠BAC+21 (∠ABC+∠ACB ) =∠BAC+21 (180°-∠BAC ) =90°+2 1 ∠BAC 例2、如图,BD、CD为△ABC的两条外角平分线, 试说明:∠D=90°-2 1 ∠A 。 解:∵BD 、CD 为角平分线 ∴∠CBD=21 ∠CBE ∠BCD =2 1 ∠BCF 又∵∠CBE 、∠BCD 为△ABC 的外角 ∴∠CBE =∠A +∠ACB ∠BCF =∠A +∠ABC ∴∠CBE +∠BCF =∠A +∠ACB +∠A +∠ABC =∠A +180° 在△BCD 中:∠D =180°-(∠CBD +∠BCD ) =180°-(21∠CBE +21 ∠BCF ) =180°-21 (∠CBE +∠BCF ) =180°-21 (∠A +180°) =90°-2 1 ∠A 【小结】通过对模型1、2的分析和证明,我们还能发现三角形两内角平分线的夹角和两外角平分线的夹角互补,即和为180°。 例3:如图,在△ABC 中,BD 为∠ABC 的平分线,CD 为∠ACE的平分线, 试说明:∠D =2 1 ∠A ; 解:∵BD 为角平分线, ∴∠CBD =2 1 ∠ABC , 又∵CD 为∠ACE 的平分线 ∴∠DCE=2 1 ∠ACE ,
角平分线的定义:从一个角的顶点引出的一条射线,把这个叫分成两个相等的角,这条射线叫做这个角的平分线 角平分线的性质定理:角平分线上的点到角两边距离相等 角平分线的判定定理:角的内部,到角两边距离相等的点,在这个角的平分线上模型一:双垂直模型基础 角的平分线上的点到这个角的两边的距离相等 【例】已知: 4 3 ,2 1∠ = ∠ ∠ = ∠,求证:AP平分BAC ∠ 解答:可证
双垂直模型进阶 【例1】已知:如图,在四边形中,CD AD AB BC =>,,BD 平分ABC ∠,求证:BAD ∠ 180=∠+C 解答: ①方法一:双垂模型 ②方法二:双等模型 可证 【例2】如图,正方形ABCD 的边长为4,DAC ∠的平分线交DC 于点E ,若点Q P ,分别是AD 和AE 上的动点,则PQ DQ +的最小值是
解答: ①方法一:双垂模型 ②方法二:双等模型【将军饮马+垂线段最短】 得证22 模型二:单垂模型基础 有垂直于角平分线的线,果断延长,就会得到一个等腰三角形 【例】如图,在ABC ?中,BE 是角平分线,BE AD ⊥,垂足为D ,求证:C ∠+∠=∠12
解答:可证 单垂模型进阶
【例1】已知:如图,在ABC ?中, AC AB BAC ==∠,90 ,BE 平分ABC ∠,BE CE ⊥,求证: BD CE 21 = 解答:可证 【例2】如图,AD CD AC AB CAD BAD ⊥>∠=∠,,于点D ,H 是BC 的中点,求证: ) (21 AC AB DH -= 解答:可证
模型三:双等模型基础 如图所示,OP 平分MON ∠,A 为OM 上一点,C 为OP 上一点,连接AC ,在射线ON 上截取OA OB =,连接BC ,易证:BOC AOC ??? 【例】如图所示,在ABC ?中,AB AC >,AD 是内角平分线,P 是AD 上异于点A 的任意一点,求证:AB AC PB PC -<-
一、角平分线的三种“模型” 模型一:角平分线+平行线→等腰三角形 如图1,过∠AOB平分线OC上的一点P,作PE∥O B,交OA于点E,则EO=EP. AAA EPCEC DFEP OBBCOFB 图1图2图3 例1 如图2,∠ABC,∠ACB的平分线相交于点F,过F作DE∥BC,交AB于点D,交AC于点E.求证:BD+EC=DE. 模型二:角平分线+垂线→等腰三角形 如图3,过∠AOB平分线OC上的一点P,作 EF⊥OC,交OA于点E,交OB于点F,则OE=OF, PE=PF. 例2 如图4,BD是∠ABC的平分线, AD⊥BD,垂足为D,求证:∠BAD=∠DAC+∠C. 模型三:角平分线+翻折→全等三角形 在△ABC中,AD是∠BAC的平分线,沿角平分线AD将△ABD往右边折叠就得到如图5的图形.此时有:△ABD≌△AB/D.此翻折相当于
在三角形的一边截取线段等于另一边,或延长一边等于另一边构造出相等的线段.用此方法可解决一些不相等的线段和差类问题. D A E AP / BC DB /BC 图5图6 例3 如图6,点P 是△ABC 的外角∠CAD 的平分线上的一点. 求证:PB+PC>AB+AC. 二、角平分线定理使用中的几种辅助线作法 一、已知角平分线,构造三角形 1、如图所示,在△ABC 中,∠ABC=3∠C ,AD 是∠BAC 的平分线,BE ⊥AD 于F 。 求证:1()2 BE AC AB =- 2、在△ABC 中,AD 平分∠BAC ,CE ⊥AD 于E .求证:∠ACE=∠B+∠ ECD . 二、已知一个点到角的一边的距离,过这个点作另一边的垂线段 1、如图所示,∠1=∠2,P 为BN 上的一点,并且PD ⊥BC 于D ,AB +BC=2BD 。 2 1F E D C B A N P E D C B A A B D C E F 图
目录 将军饮马模型 (3) 模型1:直线与两定点 (3) 模型2/角与定点 (10) 模型3两定点一定长 (15) 第十二章辅助圆 (20) 模型1 共端点,等线段模型 (20) 模型2 直角三角形共斜边模型 (23) 半角模型 (32) 模型实例 (33) 8字模型与飞镖模型 (50) 模型1:角的8字模型 (50) 模型2:角的飞镖模型 (54) 模型3 边的“8”字模型 (57) 模型4 边的飞镖模型 (58) 中点四大模型 (63) 模型1 倍长中线或类中线(与中点有关的线段)构造全等三角形 (63) 模型2 已知等腰三角形底边中点,可以考虑与顶点连接用“三线合一”. (66) 模型3 已知三角形一边的中点,可考虑中位线定理 (71) 模型4 已知直角三角形斜边中点,可以考虑构造斜边中线 (78) 二次函数 (85) 圆中的辅助线 (91) 模型1 连半径构造等腰三角形 (91) 模型2 构造直角三角形 (94) 模型3 与圆的切线有关的辅助线 (100) 相似模型 (111) 模型1:A、8模型 (111) 模型2 共边共角型 (116) 模型3 一线三等角型 (121) 模型4 倒数型 (127) 模型5 与圆有关的简单相似 (132) 模型6 相似和旋转 (136) 1.2空间几何体的三视图和直观图 (145)
1.3 空间几何体的表面积与体积 (145) 手拉手模型 (147) 模型手拉手 (147) 三垂直全等模型 (158) 模型三垂直全等模型 (158) 蚂蚁行程 (170) 模型立体图形展开的最短路径 (170) 截长补短辅助线模型 (180) 模型:截长补短 (180) 角平分线四大模型 (192) 模型1 角平分线的点向两边作垂线 (192) 模型2 截取构造对称全等 (194) 模型3 角平分线+垂线构造等腰三角形 (198) 模型4 角平分线+平行线 (200)
初中数学九大几何模型 一、手拉手模型----旋转型全等 (1)等边三角形 【条件】:△OAB 和△OCD 均为等边三角形; 【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED (2)等腰直角三角形 【条件】:△OAB 和△OCD 均为等腰直角三角形; 【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED (3)顶角相等的两任意等腰三角形 【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB 【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AED O A B C D E 图 1 O A B C D E 图 2 O A B C D E 图 1 O A C D E 图 2 O A B C D E O A B C D E 图 1 图 2
二、模型二:手拉手模型----旋转型相似 (1)一般情况 【条件】:CD ∥AB , 将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况 【条件】:CD ∥AB ,∠AOB=90° 将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ; ③ ===OA OB OC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有22 22CD AB B C AD +=+;⑥BD AC 21 S △BCD ?= 三、模型三、对角互补模型 (1)全等型-90° 【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB 【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 2 1 S S S =+= 证明提示: ①作垂直,如图2,证明△CDM ≌△CEN ②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ; ③2△OCD △OCE OC 21 S S =- O B C O A C D E O B C D E O A C D A O B C D E 图 1 A O B C D E M N 图 2 A O B C D E F 图 3 A O B C D E M N 图 4