几种插值法的应用和比较概述

插值法的应用与比较

信科1302 万贤浩 13271038

1格朗日插值法

在数值分析中，拉格朗日插值法是以法国十八世纪数学家约瑟夫·路易斯·拉格朗日命名的一种多项式插值方法.许多实际问题中都用函数来表示某种内在联系或规律，而不少函数都只能通过实验和观测来了解.如对实践中的某个物理量进行观测，在若干个不同的地方得到相应的观测值，拉格朗日插值法可以找到一个多项式，其恰好在各个观测的点取到观测到的值.这样的多项式称为拉格朗日（插值）多项式.数学上来说，拉格朗日插值法可以给出一个恰好穿过二维平面上若干个已知点的多项式函数.拉格朗日插值法最早被英国数学家爱德华·华林于1779年发现，不久后由莱昂哈德·欧拉再次发现.1795年，拉格朗日在其著作《师范学校数学基础教程》中发表了这个插值方法，从此他的名字就和这个方法联系在一起.

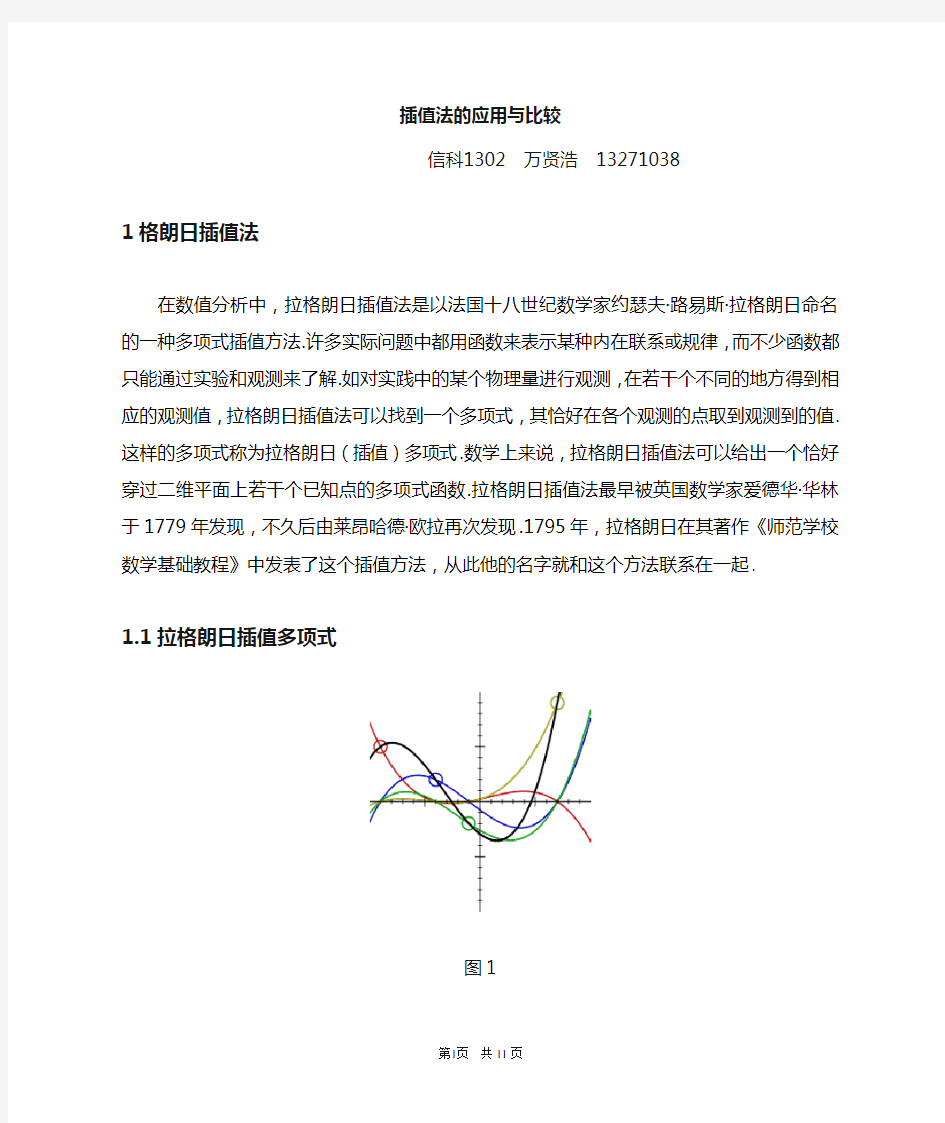
1.1拉格朗日插值多项式

图1

已知平面上四个点：(?9, 5), (?4, 2), (?1, ?2), (7, 9)，拉格朗日多项式：)(x L （黑色）穿过所有点.而每个基本多项式：)(00x l y ,)(11x l y , )(22x l y 以及)(x l y ??各穿过对应的一点，并在其它的三个点的x 值上取零.

对于给定的若1+n 个点),(00y x ,),(11y x ,………),(n n y x ，对应于它们的次数不超过n 的拉格朗日多项式L 只有一个.如果计入次数更高的多项式，则有无穷个，因为所有与L 相差

))((10x x x x --λ……)(n x x -的多项式都满足条件.

对某个多项式函数，已知有给定的1+k 个取值点：

),(00y x ,……,),(k k y x ,

其中i x 对应着自变量的位置，而i y 对应着函数在这个位置的取值.

假设任意两个不同的i x 都互不相同，那么应用拉格朗日插值公式所得到的拉格朗日插值多项式为：

)()(0

x l y x L j k

j j ∑==，

其中每个)(x l j 为拉格朗日基本多项式（或称插值基函数），其表达式为：

)()

()()()()()()()(111100,0k j k j j j j j j j k

j i i i

j i j x x x x x x x x x x x x x x x x x x x x x l --------=--=

++--≠=∏ ， 拉格朗日基本多项式()x l i 的特点是在j x 上取值为1，在其它的点i x ，j i ≠ 上取值为0. 例：设有某个多项式函数f ，已知它在三个点上的取值为：

? 10)4(=f ， ? 25.5)5(=f ， ?

1)6(=f ，

要求)18(f 的值.

首先写出每个拉格朗日基本多项式：

())64)(54()

6)(5(0----=x x x l ；

())65)(45()

6)(4(1----=x x x l ；

())

56)(46()

5)(4(2----=

x x x l ；

然后应用拉格朗日插值法，就可以得到p 的表达式（p 为函数f 的插值函数）：

)()6()()5()()4()(210x l f x l f x l f x p ++=

)

56)(46()

5)(4(1)65)(45()6)(4(25.5)64)(54()6)(5(10----?+----?+----?

=x x x x x x

)13628(4

12

+-=

x x ，

此时数值18就可以求出所需之值：11)18()18(-==p f .

1.2插值多项式的存在性与唯一性

存在性

对于给定的1+k 个点：),(),,(00k k y x y x 拉格朗日插值法的思路是找到一个在一点j x 取值为1，而在其他点取值都是0的多项式)(x l j .这样，多项式)(x l y j j 在点j x 取值为j y ， 而在其他点取值都是0.而多项式()∑==

k

j j

j x l

y x L 0

)(就可以满足

∑==++++==k

i j j j i y y x l y x L 0

000)()( ，

在其它点取值为0的多项式容易找到，例如：

)())(()(110k j j x x x x x x x x ----+- ，

它在点j x 取值为：)()()(10k j j j i x x x x x x ---+ .由于已经假定i x 两两互不相同，因此上面的取值不等于0.于是，将多项式除以这个取值，就得到一个满足“在j x 取值为1，而在其他点取值都是0的多项式”：

)

()

()()()()()()(111100k j k j j j j j j j i j j x x x x x x x x x x x x x x x x x x x

x l --------=--=++--∏

， 这就是拉格朗日基本多项式. 唯一性

次数不超过k 的拉格朗日多项式至多只有一个，因为对任意两个次数不超过k 的拉格朗日多项式：1p 和2p ，它们的差21p p -在所有1+k 个点上取值都是0,因此必然是多项式

)())((10k x x x x x x --- 的倍数.因此，如果这个差21p p -不等于0，次数就一定不小于

1+k .但是21p p -是两个次数不超过k 的多项式之差，它的次数也不超过k ，所以

021=-p p 也就是说21p p =.这样就证明了唯一性.

1.3性质

拉格朗日插值法中用到的拉格朗日基本多项式n l l l ,,,10 （由某一组n x x x <<< 10 确定）可以看做是由次数不超过n 的多项式所组成的线性空间：[]X n K 的一组基底.首先，如果存在一组系数：n λλλ,,,10 使得，

01100=+++=n n l l l P λλλ ，

那么，一方面多项式p 是满足n n x P x P x P λλλ===)(,,)(,)(1100 的拉格朗日插值多项式，另一方面p 是零多项式，所以取值永远是0.所以

010====n λλλ ，

这证明了n l l l ,,,10 是线性无关的.同时它一共包含1+n 个多项式，恰好等于[]X n K 的维数.所以n l l l ,,,10 构成了[]X n K 的一组基底.

拉格朗日基本多项式作为基底的好处是所有的多项式都是齐次的（都是n 次多项式）.

1.4优点与缺点

拉格朗日插值法的公式结构整齐紧凑，在理论分析中十分方便，然而在计算中，当插值点增加或减少一个时，所对应的基本多项式就需要全部重新计算，于是整个公式都会变化，非常繁琐.这时可以用重心拉格朗日插值法或牛顿插值法来代替.此外，当插值点比较多的时候，拉格朗日插值多项式的次数可能会很高，因此具有数值不稳定的特点，也就是说尽管在已知的几个点取到给定的数值，但在附近却会和“实际上”的值之间有很大的偏差.这类现象也被称为龙格现象，解决的办法是分段用较低次数的插值多项式.

2 重心拉格朗日插值法

重心拉格朗日插值法是拉格朗日插值法的一种改进.在拉格朗日插值法中，运用多项式

)())(()(10k x x x x x x x l ---= ，

图（2）

拉格朗日插值法的数值稳定性：如图(2)，用于模拟一个十分平稳的函数时，插值多项式的取值可能会突然出现一个大的偏差（图中的14至15中间） 可以将拉格朗日基本多项式重新写为：

∏

≠=--=

k

j

i i i j j

j x x x x x l x l ,0)

(1

)()(，

定义重心权

∏

≠=-=

k j

i i i j j x x ,0)

(1

ω，

上面的表达式可以简化为：j

j

j x x x l x l -=ω)

()(，

于是拉格朗日插值多项式变为：j k

j j

j

y x

x x l x L ∑=-=0

)

()(ω ， （1）

即所谓的重心拉格朗日插值公式（第一型）或改进拉格朗日插值公式.它的优点是当插值点的个数增加一个时，将每个j ω都除以)(1+-k j x x ，就可以得到新的重心权1+k ω，计算复杂度为

)(n O ，比重新计算每个基本多项式所需要的复杂度)(2n O 降了一个量级.

将以上的拉格朗日插值多项式用来对函数1)(≡x g 插值，可以得到：

∑

=-=?k

j j

j

x x x l x g x 0

)()(,ω，

因为1)(≡x g 是一个多项式. 因此，将)(x L 除以)(x g 后可得到：

∑

∑

==--=

k j j

j

k j j

j

x x x x x L 0

0)(ωω， （2）

这个公式被称为重心拉格朗日插值公式（第二型）或真正的重心拉格朗日插值公式.它继承了（1）式容易计算的特点，并且在代入x 值计算)(x L 的时候不必计算多项式)(x l 它的另一个优点是，结合切比雪夫节点进行插值的话，可以很好地模拟给定的函数，使得插值点个数趋于无穷时，最大偏差趋于零.同时，重心拉格朗日插值结合切比雪夫节点进行插值可以达到极佳的数值稳定性.第一型拉格朗日插值是向后稳定的，而第二型拉格朗日插值是向前稳定的，并且勒贝格常数很小.

3.分段线性插值

对于分段线性插值，我们看一下下面的情况.

3.1问题的重诉

已知2

11

)(x

x g +=

,66≤≤-x 用分段线性插值法求插值，绘出插值结果图形，并观察插值误差.

1.在[-6，6]中平均选取5个点作插值；

2.在[-6，6]中平均选取11个点作插值；

3.在[-6，6]中平均选取21个点作插值；

4.在[-6，6]中平均选取41个点作插值.

3.2问题的分析

在数值计算中，已知数据通常是离散的，如果要得到这些离散点以外的其他点的函数值，就需要根据这些已知数据进行插值.而本题只提供了取样点和原函数)(x g .分析问题求解方法如下：

（1）利用已知函数式2

11

)(x

x g +=

计算取样点X 对应的函数值Y ；将Y X ,作为两个等长的已知向量，分别描述采样点和样本值.因此被插值函数是一个单变量函数，可利用一维插值处理该数据插值问题.一维插值采用的方法通常有拉格朗日多项式插值（本题采用3次多项式插值），3次样条插值法和分段线性插值.

（2）分别利用以上插值方法求插值.以0.5个单位为步长划分区间[-6，6]，并将每一点作为插值函数的取样点.再根据插值函数计算所选取样点的函数值.最后再利用所得函数值画出相应的函数图象，并与原函数)(x g 的图象进行对比.

3.3问题的假设

为了解决上述分析所提到的问题，本题可以作出如下假设：

（1）假设原函数)(x g 仅作为求解取样点对应的样点值的函数关系式.而其他各点的函数值都是未知量，叙用插值函数计算.

（2）为了得到理想的对比函数图象，假设)(x g 为已知的标准函数.可以选取0.5个单位为步长划分区间[-6，6]，分别计算插值函数和标准函数)(x g 在该区间的取样点的函数值.画出函数图象进行对比.

3.4分段线性插值原理

给定区间[]b a ,, 将其分割成b x x x a n =<<<= 10，已知函数)(x f y =在这些插值结点的函数值为

),1,0)((n k x f y k k ==；求一个分段函数)(x I k ,使其满足：

(1) k k h y x I =)(，),1,0(n k =；

(2) 在每个区间[]1,+k k x x 上, )(x I h 是个一次函数.

易知,)(x I h 是个折线函数, 在每个区间[]1,+k k x x 上,),1,0(n k =

1111)(++++--+--=

k k

k k

k k k k k h y x x x x y x x x x x I ,

于是, )(x I h 在[]b a ,上是连续的，但其一阶导数是不连续的. 于是即可得到如下分段线性插值函数：

)()(0

x l y x I n

i i i n ∑==,

其中

????

????

?=≤≤--=≤≤--=+++---.

,0;,

;0,111

11

1

其他时舍去时，且当时舍去时，且当n i x x x x x x x i x x x x

x x x l i i i i i i i i i

i i

3.5问题的求解

在MATLAB 中实现分段线性插值，最近点插值，3次多项式插值，3次样条插值的命令

为interp 1,其调用格式为: Y 1=interp 1(X ,Y ,X 1，’method ’)

函数根据X ,Y 的值，计算函数在X 1处的值.X ,Y 是两个等长的已知向量，分别描述采样点和样本值，X 1是一个向量或标量，描述欲插值点，Y 1是一个与X 1等长的插值结果.method 是插值方法，包括：

linear ：分段线性插值.它是把与插值点靠近的两个数据点用直线连接，然后在直线让选取对应

插值点的数.

nearest ：近点插值法.根据已知两点间的插值点与这两点间的位置远近插值.当插值点距离前点

远时,取前点的值,否则取后点的值.

cubic ：3次多项式插值.根据已知数据求出一个3次多项式，然后根据多项式进行插值. spline ：3次样条插值.在每个分段（子区间）内构造一个3次多项式，使其插值函数除满足插

值条件外，还要求个节点处具有光滑条件.再根据已知数据求出样条函数后,按照样条函数插值.

运用Matlab 工具软件编写代码，并分别画出图形如下： (一)在[-6，6]中平均选取5个点作插值：

-10-5

05

10

00.20.40.60.81分段线性插值

g(x)y1-10

-5

0510-0.50

0.513次样条插值

g(x)y2

-10

-5

5

10

00.20.40.60.81最近点插值

g(x)y3

-10

-5

0510

00.20.40.60.813次多项式插值

g(x)y4

（二）在[-6，6]中平均选取11个点作插值：

-10-5

05

1000.20.40.60.81

-10

-5

051000.20.40.60.81

-10

-5

5

10

00.20.40.60.81最近点插值

-10

-5

0510

00.20.40.60.813次多项式插值

g(x )y1

g(x )y2

g(x )y3

g(x )y4

（三）在[-6，6]中平均选取21个点作插值：

-10-5

05

1000.20.40.60.81分段线性插值

-10

-5

5

1000.20.40.60.813次样条插值

-10

-5

5

10

00.20.40.60.81最近点插值

-10

-5

5

10

00.20.40.60.813次多项式插值

g(x )y1

g(x )y2

g(x )y3

g(x )y4

（四）在[-6，6]中平均选取41个点作插值

-10-5

05

1000.20.40.60.81

g(x )y1

-10

-5

051000.20.40.60.81

g(x )y2

-10

-5

5

10

00.20.40.60.81最近点插值

g(x )y3

-10

-5

0510

00.20.40.60.813次多项式插值

g(x )y4

3.6 分段插值方法的优劣性分析

从以上对比函数图象可以看出，分段线性插值其总体光滑程度不够.在数学上，光滑程度的定量描述是函数(曲线) 的k 阶导数存在且连续，则称该曲线具有k 阶光滑性.一般情况下，阶数越高光滑程度越好.分段线性插值具有零阶光滑性，也就是不光滑.3次样条插值就是较低次数的多项式而达到较高阶光滑性的方法.总体上分段线性插值具有以下特点：

优点: 1.分段线性插值在计算上具有简洁方便的特点.

2.分段线性插值与3次多项式插值函数在每个小区间上相对于原函数都有很强的收敛性，（舍入误差影响不大），数值稳定性好且容易在计算机上编程实现等优点

缺点: 分段线性插值在节点处具有不光滑性的缺点(不能保证节点处插值函数的导数连

续)，从而不能满足某些工程技术上的要求.而3次样条插值却具有在节点处光滑的特点.

牛顿插值法原理及应用

牛顿插值法 插值法是利用函数f (x)在某区间中若干点的函数值，作出适当的特定函数，在这些点上取已知值，在区间的其他点上用这特定函数的值作为函数f (x)的近似值。如果这特定函数是多项式，就称它为插值多项式。当插值节点增减时全部插值基函数均要随之变化，这在实际计算中很不方便。为了克服这一缺点，提出了牛顿插值。牛顿插值通过求各阶差商，递推得到的一个公式： f(x)=f[x0]+f[x0,x1](x-x0)+f[x0,x1,x2](x-x0)(x-x1)+...f[x0,...xn](x-x0 )...(x-xn-1)+Rn(x)。 插值函数 插值函数的概念及相关性质[1] 定义：设连续函数y-f(x) 在区间[a,b]上有定义，已知在n+1个互异的点 x0,x1,…xn上取值分别为y0,y1,…yn （设a≤ x1≤x2……≤xn≤b)。若在函数类中存在以简单函数P(x) ，使得P(xi)=yi,则称P(x) 为f(x)的插值函数. 称x1,x2,…xn 为插值节点，称[a,b]为插值区间。 定理：n次代数插值问题的解存在且唯一。

牛顿插值法C程序 程序框图#include void main() { float x[11],y[11][11],xx,temp,newton; int i,j,n; printf("Newton插值:\n请输入要运算的值:x="); scanf("%f",&xx); printf("请输入插值的次数(n<11):n="); scanf("%d",&n); printf("请输入%d组值:\n",n+1); for(i=0;i

空间插值方法汇总

空间插值方法汇总 Inverse Distance to a Power（反距离加权插值法） Kriging（克里金插值法） Minimum Curvature（最小曲率） Modified Shepard's Method（改进谢别德法） Natural Neighbor（自然邻点插值法） Nearest Neighbor（最近邻点插值法） Polynomial Regression（多元回归法） Radial Basis Function（径向基函数法） Triangulation with Linear Interpolation（线性插值三角网法） Moving Average（移动平均法） Local Polynomial（局部多项式法） 1、距离倒数乘方法 距离倒数乘方格网化方法是一个加权平均插值法，可以进行确切的或者圆滑的方式插值。方次参数控制着权系数如何随着离开一个格网结点距离的增加而下降。对于一个较大的方次，较近的数据点被给定一个较高的权重份额，对于一个较小的方次，权重比较均匀地分配给各数据点。计算一个格网结点时给予一个特定数据点的权值与指定方次的从结点到观测点的该结点被赋予距离倒数成比例。当计算一个格网结点时，配给的权重是一个分数，所有权重的总和等于1.0。当一个观测点与一个格网结点重合时，该观测点被给予一个实际为 1.0 的权重，所有其它观测点被给予一个几乎为 0.0 的权重。换言之，该结点被赋给与观测点一致的值。这就是一个准确插值。距离倒数法的特征之一是要在格网区域内产生围绕观测点位置的"牛眼"。用距离倒数格网化时可以指定一个圆滑参数。大于零的圆滑参数保证，对于一个特定的结点，没有哪个观测点被赋予全部的权值，即使观测点与该结点重合也是如此。圆滑参数通过修匀已被插值的格网来降低"牛眼"影响。 2、克里金法 克里金法是一种在许多领域都很有用的地质统计格网化方法。克里金法试图那样表示隐含在你的数据中的趋势，例如，高点会是沿一个脊连接，而不是被牛眼形等值线所孤立。克里金法中包含了几个因子：变化图模型，漂移类型和矿块效应。 3、最小曲率法 最小曲率法广泛用于地球科学。用最小曲率法生成的插值面类似于一个通过各个数据值的，具有最小弯曲量的长条形薄弹性片。最小曲率法，试图在尽可能严格地尊重数据的同时，生成尽可能圆滑的曲面。使用最小曲率法时要涉及到两个参数：最大残差参数和最大循环次数参数来控制最小曲率的收敛标准。 4、多元回归法 多元回归被用来确定你的数据的大规模的趋势和图案。你可以用几个选项来确定你需要的趋势面类型。多元回归实际上不是插值器，因为它并不试图预测未知的 Z 值。它实际上是一个趋势面分析作图程序。使用多元回归法时要涉及到曲

arcgis空间内插值教程

GIS空间插值（局部插值方法）实习记录 一、空间插值的概念和原理 当我们需要做一幅某个区域的专题地图，或是对该区域进行详细研究的时候，必须具备研究区任一点的属性值，也就是连续的属性值。但是，由于各种属性数据（如降水量、气温等）很难实施地面无缝观测，所以，我们能获取的往往是离散的属性数据。例如本例，我们现有一幅山东省等降雨量图，但是最终目标是得到山东省降水量专题图（覆盖全省，统计完成后，各地均具有自己的降雨量属性）。 空间插值是指利用研究区已知数据来估算未知数据的过程，即将离散点的测量数据转换为连续的数据曲面。利用空间插值，我们就可以通过离散的等降雨量线，来推算出山东省各地的降雨量了。 二、空间插值的几种方法及本次实习采用的原理和方法 –整体插值方法 ?边界内插方法 ?趋势面分析 ?变换函数插值 –局部分块插值方法 ?自然邻域法 ?移动平均插值方法：反距离权重插值 ?样条函数插值法（薄板样条和张力样条法） ?空间自协方差最佳插值方法：克里金插值 ■局部插值方法的控制点个数与控制点选择问题 局部插值方法用一组已知数据点（我们将其称为控制点）样本来估算待插值点（未知点）的值，因此控制点对该方法十分重要。 为此，第一要注意的是控制点的个数。控制点的个数与估算结果精确程度的关系取决于控制点的分布与待插值点的关系以及控制点的空间自相关程度。为了获取更精确的插值结果，我们需要着重考虑上述两点因素（横线所示）。 第二需要注意的是怎样选择控制点。一种方法是用离估算点最近的点作为控制点；另一种方法是通过半径来选择控制点，半径的大小必须根据控制点的分布来调整。 S6、按照不同方法进行空间插值，并比较各自优劣 打开ArcToolbox——Spatial Analyst 工具——插值，打开插值方法列表，如下图：

常见的插值方法及其原理

常见的插值方法及其原理 这一节无可避免要接触一些数学知识，为了让本文通俗易懂，我们尽量绕开讨厌的公式等。为了进一步的简化难度，我们把讨论从二维图像降到一维上。 首先来看看最简单的‘最临近像素插值’。 A,B是原图上已经有的点，现在我们要知道其中间X位置处的像素值。我们找出X位置和A,B位置之间的距离d1,d2，如图，d2要小于d1,所以我们就认为X处像素值的大小就等于B处像素值的大小。 显然，这种方法是非常苯的，同时会带来明显的失真。在A,B中点处的像素值会突然出现一个跳跃，这就是为什么会出现马赛克和锯齿等明显走样的原因。最临近插值法唯一的优点就是速度快。 图10，最临近法插值原理 接下来是稍微复杂点的‘线性插值’（Linear） 线性插值也很好理解，AB两点的像素值之间，我们认为是直线变化的，要求X点处的值，只需要找到对应位置直线上的一点即可。换句话说，A,B间任意一点的值只跟A,B有关。由于插值的结果是连续的，所以视觉上会比最小临近法要好一些。线性插值速度稍微要慢一点，但是效果要好不少。如果讲究速度，这是个不错的折衷。 图11，线性插值原理

其他插值方法 立方插值，样条插值等等，他们的目的是试图让插值的曲线显得更平滑，为了达到这个目的，他们不得不利用到周围若干范围内的点，这里的数学原理就不再详述了。 图12，高级的插值原理 如图，要求B,C之间X的值，需要利用B,C周围A,B,C,D四个点的像素值，通过某种计算，得到光滑的曲线，从而算出X的值来。计算量显然要比前两种大许多。 好了，以上就是基本知识。所谓两次线性和两次立方实际上就是把刚才的分析拓展到二维空间上，在宽和高方向上作两次插值的意思。在以上的基础上，有的软件还发展了更复杂的改进的插值方式譬如S-SPline, Turbo Photo等。他们的目的是使边缘的表现更完美。

高中化学-简单分类法及其应用分层练习

高中化学-简单分类法及其应用分层练习 层级一 学业达标练 1．碳酸钠俗名纯碱，下面是对纯碱采用不同分类法的分类，其中正确的是( ) ①碱 ②含氧酸盐 ③钠盐 ④碳酸盐 A ．①②③ B ．①③④ C ．①②④ D ．②③④ 解析：选D 纯碱若采用交叉分类法分别属于含氧酸盐、钠盐、碳酸盐。 2．符合如图中阴影部分的物质是( ) A ．NaHCO 3 B ．Cu 2(OH)2CO 3 C ．NaCl D ．Na 2CO 3 解析：选D A 项属于酸式盐；B 项为碱式盐、铜盐；C 项不属于碳酸盐。 3．对于化学反应A ＋B===C ＋D 的下列说法中，正确的是( ) A ．若生成物C 、D 有一种为单质，该反应一定是置换反应 B ．若生成物C 、D 分别为两种沉淀，A 、B 有可能为盐和碱 C ．若生成物C 、D 是盐和水，则A 、B 一定是酸和碱 D ．若生成物C 、D 是两种化合物，则A 、B 一定是化合物 解析：选B 由反应CO ＋CuO =====△ CO 2＋Cu 知，A 项错误；由反应Ba(OH)2 ＋CuSO 4===BaSO 4↓＋Cu(OH)2↓知，B 项正确；由反应CuO ＋H 2SO 4===CuSO 4＋H 2O 知，C 项错误；由反应CH 4＋2O 2点燃,CO 2＋2H 2O 知，D 项错误。 4．Na 2O 、NaOH 、Na 2CO 3、NaCl 、Na 2SO 4可按某种标准划为同一类物质，下列分类标准正确的是(已知Na 2O 与水反应生成NaOH)( ) ①钠的化合物 ②能与硝酸反应的物质 ③可溶于水的物质 ④水溶液导电 ⑤钠盐 ⑥钠的含氧化合物

几种常用的插值方法

几种常用的插值方法 数学系 信息与计算科学1班 李平 指导老师：唐振先 摘要:插值在诸如机械加工等工程技术和数据处理等科学研究中有许多直接的应用,在很多领域都要用插值的办法找出表格和中间值,插值还是数值积分微分方程数值解等数值计算的基础。本文归纳了几种常用的插值方法,并简单分析了其各自的优缺点。 关键词:任意阶多项式插值,分段多项式插值。 引言:所谓插值,通俗地说就是在若干以知的函数值之间插入一些未知函数值,而插值函数的类型最简单的选取是代数多项式。用多项式建立插值函数的方法主要用两种：一种是任意阶的插值多项式,它主要有三种基本的插值公式：单项式,拉格朗日和牛顿插值；另一种是分段多项式插值,它有Hermite 和spine 插值和分段线性插值。 一．任意阶多项式插值： 1.用单项式基本插值公式进行多项式插值： 多项式插值是求通过几个已知数据点的那个n-1阶多项式,即P n-1(X)=A 1+A 2X+…A n X n-1,它是一个单项式基本函数X 0,X 1…X n-1的集合来定义多项式,由已知n 个点（X,Y ）构成的集合,可以使多项式通过没数据点,并为n 个未知系数Ai 写出n 个方程,这n 个方程组成的方程组的系数矩阵为Vandermonde 矩阵。 虽然这个过程直观易懂,但它都不是建立插值多项式最好的办法,因为Vandermonde 方程组有可能是病态的,这样会导致单项式系数不确定。另外,单项式中的各项可能在大小上有很大的差异,这就导致了多项式计算中的舍入误差。 2.拉格朗日基本插值公式进行插值： 先构造一组插值函数L i （x ） =011011()()()() ()()()() i i n i i i i i i n x x x x x x x x x x x x x x x x -+-+--------L L L L ，其中i=0，… n.容易看出n 次多项式L i （x ）满足L i （x ）=1，（i=j ）；L i （x ）=0，（i ≠j ），其中

三次样条插值方法的应用

CENTRAL SOUTH UNIVERSITY 数值分析实验报告

三次样条插值方法的应用 一、问题背景 分段低次插值函数往往具有很好的收敛性，计算过程简单，稳定性好，并且易于在在电子计算机上实现，但其光滑性较差，对于像高速飞机的机翼形线船体放样等型值线往往要求具有二阶光滑度，即有二阶连续导数，早期工程师制图时，把富有弹性的细长木条（即所谓的样条）用压铁固定在样点上，在其他地方让他自由弯曲，然后沿木条画下曲线，称为样条曲线。样条曲线实际上是由分段三次曲线并接而成，在连接点即样点上要求二阶导数连续，从数学上加以概括就得到数学样条这一概念。下面我们讨论最常用的三次样条函数及其应用。 二、数学模型 样条函数可以给出光滑的插值曲线（面），因此在数值逼近、常微分方程和偏微分方程的数值解及科学和工程的计算中起着重要的作用。 设区间[]b ,a 上给定有关划分b x x n =<<<= 10x a ，S 为[]b ,a 上满足下面条件的函数。 ● )(b a C S ,2∈； ● S 在每个子区间[]1,+i i x x 上是三次多项式。 则称S 为关于划分的三次样条函数。常用的三次样条函数的边界条件有三种类型： ● Ⅰ型 ()()n n n f x S f x S ''0'',==。 ● Ⅱ型 ()()n n n f x S f x S ''''0'''',==，其特殊情况为()()0''''==n n x S x S 。 ● Ⅲ型 ()() 3,2,1,0,0==j x S x S n j j ，此条件称为周期样条函数。 鉴于Ⅱ型三次样条插值函数在实际应用中的重要地位，在此主要对它进行详细介绍。 三、算法及流程 按照传统的编程方法，可将公式直接转换为MATLAB 可是别的语言即可；另一种是运用矩阵运算，发挥MATLAB 在矩阵运算上的优势。两种方法都可以方便地得到结果。方法二更直观，但计算系数时要特别注意。这里计算的是方法一的程序，采用的是Ⅱ型边界条件，取名为spline2.m 。 Matlab 代码如下： function s=spline2(x0,y0,y21,y2n,x) %s=spline2(x0,y0,y21,y2n,x) %x0,y0 are existed points,x are insert points,y21,y2n are the second

简单分类法及其应用

实用文档 简单分类法及其应用 一．选择题 1．2011年2月22日新西兰发生6.3级地震，地震之后，水和食物的短缺是最致命的．水、帐篷和高营养、易吸收的食品将有助于灾区民众顺利度过难关．水的化学式为H 2O ，由此判断H 2O 属于化合物中的( ) A ．氧化物 B ．酸 C ．盐 D ．碱 2．物质分类是化学研究的重要方法之一．化学工作者经常根据物质的组成对物质进行分类研究．近年来发现，在金星大气层中存在三氧化二碳．下列物质与它属于同类的是( ) A ．H 2、O 3 B ．H 2SO 4、H 2CO 3 C ．SO 2、NO D ．Na 2SO 3、KClO 3 3．下列反应方程式中有一个与其他三个在分类上不同，这个反应是( ) A ．3Fe ＋2O 2=====点燃 Fe 3O 4 B ．C ＋CO 2=====△ 2CO C ．NH 4HCO 3=====△ NH 3↑＋H 2O ＋CO 2↑ D ．Na 2CO 3＋CO 2＋H 2O===2NaHCO 3 4．符合图中阴影部分的物质是( )

A．NaHCO3B．Cu2(OH)2CO3 C．NaCl D．Na2CO3 5．下列各物质的分类、名称(或俗名)、化学式都正确的是( ) 分类名称(或俗名)化学式 A碱性氧化物氧化铁FeO B酸性氧化物碳酸气CO C酸硫酸H2S D盐纯碱Na2CO3 6.2010年春天网上报导问题奶粉又流入社会，某品牌 NNNH2NNH2NH2婴幼儿奶粉中含有三聚氰胺(如图)，它对婴幼儿泌尿系统有很大危害，下列关于三聚氰胺所属物质类别的说法正确的是( ) A．三聚氰胺属于单质 B．三聚氰胺属于氢化物 C．三聚氰胺属于化合物 D．三聚氰胺属于混合物 7．对下列物质分类全部正确的是( ) 实用文档

插值法在管理决策中的应用及其Matlab实现

插值法在管理决策中的应用及其Ｍａｔｌａｂ实现 张英俊，孙大宁＊，张亚娟 （北方工业大学理学院，北京１００１４４） 摘 要：利用插值曲线，即三次样条插值和立方插值法来比较分析随机网络评审法中两个随机变量之间的相关 性．经分析表明，立方插值不仅是分析相关性的实用曲线工具，而且利用Ｍａｔｌａｂ所构造的函数有足够的光滑性、平顺性，且图像在考察变量的相关性时具有直观性的优点，因此对它的应用研究非常有价值． 关键词：插值 Ｍａｔｌａｂ程序相关性 中图分类号：Ｏ２９；ＴＢ１１５文献标识码：Ａ文章编号：１６７４－０８７４（２００８）０３－００４０－０３ 收稿日期：２００８－０１－１５ 作者简介：张英俊（１９８２－），女，山西平遥人，在读硕士，研究方向：风险决策；＊孙大宁，男，教授，通讯作者． 随机网络评审法是基于随机网络和计算机仿真的一种随机型的定量评估方法，它是以风险评审技术（简称ＶＥＲＴ）为基础的，ＶＥＲＴ是一种计算机仿真技术，它把网络理论，仿真原理和概率论综合起来，其特点之一就是在各种信息不完全，不充分和不肯定的情况下，对各种工程系统和工程项目的发展计划有关的时间Ｔ（周期或工作量），费用Ｃ（耗费、成本或投入），功能Ｐ（性能、效益或输出等）三种指标来描述，从而描述决策分析对象应达到的目标．一般情况下，在进行风险决策分析时为了有利于模型的建立和使分析计算工作更快更有效，我们需要对网络中各个节点上相应随机参数的频数直方图以及３个参数中任意两者之间的相关性进行分析．在处理我国飞机预研计划这一课题发展起来的 ＳＮＳＳ系统是采用Ｆｏｒｔｒａｎ７７语言编写的［１］，以卡片形式进行输入输出的，在输出直方图以及进行时间、 费用、效益三者中任两者之间相互关系的计算上不是很直观、很简洁．其实两个随机参数之间的这种函数关系，在数值分析中有许多的方法可以求得，但是哪种方法能更直观、更合乎实际地给出反映这种相关性的平滑曲线呢？本文所选的插值方法能够较好地满足这一要求． １插值方法的选择及其数学原理 插值是已知某函数在若干离散点上的函数值或者导数信息，通过求解该函数中待定形式的插值函数以及待定系数，使得该函数在给定离散点上满足约束．也即要求通过平面上已知ｎ个点（ｘｉ，ｙｉ），ｉ＝ １，２，…，ｎ作一条光滑的曲线，完成这项工作的方 法有多种，如拉格朗日插值、埃尔米特插值和分段 插值等．实际表明，拉格朗日插值和埃尔米特插值函数对于数据较多且具有随机性的变量相关性分析，做一个高次插值多项式是不理想的，因为它带有近似性，且计算也相当复杂．而分段插值是克服高次插值的Ｒｕｎｇｅ现象而提出的，只能保证曲线的连续性，却不能保证曲线的光滑性．但是在生产和科学实验中，对所做的插值曲线既要简单，又要在曲线的连接处比较光滑，即所作的分段插值函数在分段上要求多项式次数低，而在节点上不仅连续，还存在连续的低阶导数，我们把满足这样条件的插值函数，称为样条插值函数，它所对应的曲线称为样条曲线，其节点称为样点，这种插值方法称为样条插值［２］． ２ 应用举例 ２．１ 资料说明 某企业的领导和管理者，得知与其竞争的另一 企业正在研制一种新产品，一旦这种新产品研制成功，将给另一企业带来销售市场上的绝对优势，如 第２４卷第３期山西大同大学学报（自然科学版） Ｖｏｌ．２４．Ｎｏ．３２００８年６月 ＪｏｕｒｎａｌｏｆＳｈａｎｘｉＤａｔｏｎｇＵｎｉｖｅｒｓｉｔｙ（ＮａｔｕｒａｌＳｃｉｅｎｃｅ） Ｊｕｎ．２００８

插值法在图像处理中的运用要点

插值方法在图像处理中的应用 作者： 专业姓名学号 控制工程陈龙斌 控制工程陈少峰 控制工程殷文龙 摘要 本文介绍了插值方法在图像处理中的应用。介绍了典型的最近邻插值、双线性插值、双三次插值、双信道插值、分形插值的原理。以分形插值为重点，在图像放大领域用MATLAB进行仿真，并与其它方法的结果做了比对。指出了各种方法的利弊，期待更进一步的研究拓展新的算法以及改进现有算法。

一、引言 人类通过感觉器官从客观世界获取信息，而其中一半以上的信息都是通过视觉获得的。图像作为人类视觉信息传递的主要媒介，具有声音、语言、文字等形式无法比拟的优势，给人以具体、直观的物体形象。在数字化信息时代，图像处理已经成为重要的数据处理类型。数字图像比之传统的模拟图像处理有着不可比拟的优势。一般采用计算机处理或者硬件处理，处理的内容丰富，精度高，变通能力强，可进行非线性处理。但是处理速度就会有所不足。图像处理的主要内容有：几何处理、算术处理、图像增强、图像复原、图像重建、图像编码、图像识别、图像理解等。以上这些图像处理大体上可分为图像的像质改善、图像分析和图像重建三大部分。 日常生活中，越来越多的领域需要高分辨率图像，采用图像插值技术来提高数字图像的分辨率和清晰度，从软件方面进行改进就具有十分重要的实用价值。多媒体通信在现代网络传输中扮演重要角色，因此插值放大提高图像分辨率是一个非常重要的问题。此外，图像变换被广泛用于遥感图像的几何校正、医学成像以及电影、电视和媒体广告等影像特技处理中。在进行图像的一些几何变换时，通常都会出现输出像素坐标和输入栅格不重合的现象，也必须要用到图像插值。图像插值是图像处理中图像重采样过程中的重要组成部分，而重采样过程广泛应用于改善图像质量、进行有损压缩等，因而研究图像插值具有十分重要的理论意义和实用价值。 图像插值是一个数据再生过程。由原始图像数据再生出具有更高分辨率的图像数据。分为图像内插值和图像间插值。前者指将一幅较低分辨率的图像再生出一幅较高分辨率的图像。后者指在若干幅图像之间再生出几幅新的图像。插值过程就是确定某个函数在两个采样点之间的数值时采用的运算过程．通常是利用曲线拟合的方法进行插值算法，通过离散的输入采样点建立一个连续函数，用这个重建的函数求出任意位置处的函数值，这个过程可看作是采样的逆过程。 20世纪40年代末，香农提出了信息论，根据采样定理，若对采样值用sinc函数进行插值，则可准确地恢复原函数，于是sinc函数被接受为插值函数，也称为理想插值函数。理想插值函数有两个缺点： （1）它虽然对带限信号可以进行无错插值，但实际中带限信号只是一小部分信号。 （2）sinc函数的支撑是无限的，而没有函数既是带限的，又是紧支撑的。 为了解决这个问题，经典的办法是刚窗函数截断sinc函数，这个窗函数必须在0剑l 之间为正数，在l到2之间为负数。sinc函数对应的是无限冲激响应，不适于有限冲激相应来进行局部插值。对数字图像来说，对图像进行插值也称为图像的重采样。它分为两个步骤：将离散图像插值为连续图像以及对插值结果图像进行采样。 经典的图像插值算法是利用邻近像素点灰度值的加权平均值来计算未知像素点处的灰度值，而这种加权平均一般表现表现为信号的离散采样值与插值基函数之间的二维卷积。这种基于模型的加权平均的图像插值方法统称为线性方法。经典的插值方法有：最近邻域法，双线性插值，双三次B样条插值，双三次样条插值，sinc函数等。线性方法，它们一个共同点就是，所有这些基函数均是低通滤波器，对数据中的高频信息都具有滤除和抑制效应，因

五种插值法的对比研究开题报告

五种插值法的对比研究 1. 选题依据 1.1 选题背景 插值法是一种古老的数学方法，插值法历史悠久。据考证，在公元六世纪时， 我国焯(zhuo) 已经把等距二次插值法应用于天文计算。十七世纪时，Newton 和 Gregory(格雷格里) 建立了等距节点上的一般插值公式，十八世纪时，Lagrange(拉格朗日) 给出了更一般的非等距节点插值公式。 而它的基本理论是在微积分产生以后逐渐完善的，它的实际应用也日益增多，特别是在计算机工程中。许多库函数的计算实际上归结于对逼近函数的计算。 1.2 研究的目的和意义 插值法是数值分析中最基本的方法之一。 在实际问题中碰到的函数是各种各样的，有的甚至给不出表达式，只提供了一些离散数据，例如，在查对数表时， 要查的数据在表中找不到，就先找出它相邻的数，再从旁边找出它的修正值， 按一定关系把相邻的数加以修正，从而找出要找的数，这种修正关系实际上就是一种插值。 在实际应用中选用不同类型的插值函数，逼近的效果也不同。在数值计算方法中，我们学习过五种基本的插值方法，即Lagrange 插值、Newton 插值、分段线性插值、分段三次Hermite 插值、样条插值函数。所以通过从这五种插值法的基本思想、特征、性质和具体实例入手，探讨五种插值法的优缺点和适用围，让学习者能够迅速而准确的解决实际问题，掌握插值法的应用。 2. 研究的方法 从具体实例入手并结合Matlab 在科学计算中的优势，通过实验对它们的精度和效率进行比较分析。 3. 论文结构 3.1 论文的总体结构 第一部分 导言 主要介绍选题的背景、目的及意义、研究现状、文献综述等。 第二部分 五种插值法的基本思想、性质及特点 在数值计算方法中，插值法是计算方法的基础，数值微分、数值积分和微分方程数值解都建立在此基础上。 插值问题的提法是：已知f(x)(可能未知或非常复杂函数)在彼此不同的n+1 个实点0x ,1x ,…n x 处的函数值是f(0x )，f(1x )，…,f(n x )，这时我们简单的说f(x)有n+1 个 离散数据对0n i i )}y ,{(x i .要估算f(x)在其它点x 处的函数值，最常见的一种办法就是插 值，即寻找一个相对简单的函数y(x)，使其满足下列插值条件：y(i x )=f(i x )，i=0,1,…,n.，并以y(x)作为f(x)的近似值.其中y(x)称为插值函数，f(x)称为被插函数。

几种插值法比较与应用

多种插值法比较与应用 （一）Lagrange 插值 1． Lagrange 插值基函数 n+1个n 次多项式 ∏ ≠=--=n k j j j k j k x x x x x l 0)( n k ,,1,0ΛΛ= 称为Lagrange 插值基函数 2． Lagrange 插值多项式 设给定n+1个互异点))(,(k k x f x ，n k ,,1,0ΛΛ=，j i x x ≠，j i ≠，满足插值条件 )()(k k n x f x L =，n k ,,1,0ΛΛ= 的n 次多项式 ∏∏ ∏=≠==--==n k n k j j j k j k k n k k n x x x x x f x l x f x L 0 00 ))(()()()( 为Lagrange 插值多项式，称 ∏=+-+=-=n j j x n n x x n f x L x f x E 0 )1()()!1()()()()(ξ 为插值余项，其中),()(b a x x ∈=ξξ （二）Newton 插值 1．差商的定义 )(x f 关于i x 的零阶差商 )(][i i x f x f = )(x f 关于i x ，j x 的一阶差商

i j i j j i x x x f x f x x f --= ][][],[ 依次类推，)(x f 关于i x ，1+i x ，……，k i x +的k 阶差商 i k i k i i k i i k i i i x x x x f x x f x x x f --= +-+++++] ,,[],,[],,,[111ΛΛΛΛΛ 2． Newton 插值多项式 设给定的n+1个互异点))(,(k k x f x ，n k ,,1,0ΛΛ=，j i x x ≠，j i ≠， 称满足条件 )()(k k n x f x N =，n k ,,1,0ΛΛ= 的n 次多项式 )()](,,,[)](,[][)(10100100---++-+=n n n x x x x x x x f x x x x f x f x N ΛΛΛΛΛ 为Newton 插值多项式，称 ],[,)(],,,[)()()(010b a x x x x x x f x N x f x E n j j n n ∈-=-=∏=ΛΛ 为插值余项。 （三）Hermite 插值 设],[)(1b a C x f ∈，已知互异点0x ，1x ，…，],[b a x n ∈及所对应的函数值为0f ，1f ，…，n f ，导数值为'0f ，'1f ，…，'n f ，则满足条件 n i f x H f x H i i n i i n ,,1,0,)(,)(''1212Λ===++ 的12+n 次Hermite 插值多项式为 )()()(0 '12x f x f x H j n j j j n j i n βα∏∏=++= 其中 )())((,)]()(21[)(2 2'x l x x x l x l x x x j j j j j j j j ---=βα

简单分类法及其应用

教学板块 人 板块一 生活中的分类及分类定义 任务1.1 认识并能举出生活中的各种分类，体会并感受生活中的分类意义。 任务1.2 认识并理解分类的标准及重要性，明确分类的定义 活动1.1,1：进行“记忆游戏”，看同学们在20s 内可以记住多少个屏幕上的内容 活动1.1.2：例举生活中的各种分类的例子，感受分类的意义 活动2,1.1：例举生活中衣物整理的例子，看同学如何整理分类？ 活动 2.1.2：学生讨论在生活中如何将物质进行分类的？并学习物质分类的定义。 板块二 化学中的常用分 类 任务2.1 感受单一分类方法的缺点和不足 任务2.2 掌握交叉分类方法，并能正确的应用两种方法对物质进行分类 任务2.4 思考并回顾化学中常用的分类方法，以及理解这节课对物质分类活动2.1.1 ：对K 2SO 4 、Na 2CO 3、K 2CO 3、Na 2SO 4这四种物质分类。 活动2.2.:1：给体育明星进行连线 活动2.2.2：用交叉法对K 2SO 4 、Na 2CO 3、K 2CO 3、Na 2SO 进行连线，分类 活动2.4,1:回顾这节课所学的分类方法，体会分类标准及意义。 任务2.3 掌握树状分类方法，并能正确的应用两种方法对物质进行分类 活动2.3.:1：回忆初中所学习的各种物质类别的概念。 活动 2.3.:2：学习树状分类法，并对物质、纯净物、单质、化合物、氧化物、酸、碱、盐、混合物这几个概念进行分类

物质的分类（课时一） §2.1物质的分类——简单分类法及其应用教学设计 课题简单分类法及其应用课型新知识课 授课人授课班级 教材分析本节教学内容位于新课标人教版高中化学必修1第二章《化学物质及其变化》第一节《物质的分类》。课标在本节的要求是“能根据物质的组成和性质对物 质进行分类，并尝试用不同的方法对物质进行分类”。 简单分类法是新课程背景下化学教学教材所增添的“新”内容之一。在初高中 的学习中，贯穿中学化学的学习，对中学化学的教学起到了“承前启后”的作 用。学生既可以对初中所学的化学知识进行分类整理，又可以在学生掌握科学 的方法后对以后的化学知识进行更加系统和有效地学习。从新课程内容编排的 角度看，新课程以元素及其化合物的类别作为知识编排的一条主线，每一种类 别的元素及其化合物都是从典型的元素及其化合物作为切入点展开，这样可以 举一反三，让学生的学习变得更加具有调理型。通过本章节的学习，学生对科 学分类方法有了更深刻的认识，也有利于学生自身科学素养的培养。以共性的 角度出发来学习化学，学生会对化学知识体系的建构更加完备。 学生分析教学对象是高一的学生，有一定的生活经验和知识基础，并已经有了生活中对很多事物是分类的概念。在初中化学的学习中，学生已掌握了四种基本反应， 以及酸、碱、盐、氧化物等化学的基本内容，但却没有概括过这些物质间所存 在的共性，以及物质与物质间的转化规律。由此学生对初中学习的基本反应的 本质以及物质的概念还未完全的掌握。通过物质的分类这节课的学习，学生可 以将初中化学学习的知己进行归纳与总结，形成系统的分类观，由此更有利于 对高中化学的学习。 【知识与技能】 1.能根据物质的组成和性质对物质进行分类; 2.学习几种分类方法，并掌握交叉分类法和树状分类法； 3.可根据物质之间的变化规律对一些简单的基本化学反应分类。 【过程与方法】 1.通过学生对日常生活中对物质的分类方法，运用观察，比较，归纳的方法，

插值法的原理

《财务管理》教学中插值法的快速理解和掌握 摘要在时间价值及内部报酬率计算时常用到插入法，但初学者对该方法并不是很容易理解和掌握。本文根据不同情况分门别类。利用相似三角形原理推导出插入法计算用公式。并将其归纳为两类：加法公式和减法公式，简单易懂、理解准确、便于记忆、推导快捷。 关键词插入法；近似直边三角形；相似三角形 时间价值原理正确地揭示了不同时点上资金之间的换算。是财务决策的基本依据。为此，财务人员必须了解时间价值的概念和计算方法。但在教学过程中。笔者发现大多数教材插值法(也叫插入法)是用下述方法来进行的。如高等教育出版社2000年出版的《财务管理学》P62对贴现期的。 事实上，这样计算的结果是错误的。最直观的判断是：系数与期数成正向关系。而4.000更接近于3.791。那么最后的期数n应该更接近于5，而不是6。正确结果是：n=6-0.6=5.4(年)。由此可见，这种插入法比较麻烦，不小心时还容易出现上述错误。 笔者在教学实践中用公式法来进行插值法演算，效果很好，现分以下几种情况介绍其原理。 一、已知系数F和计息期n。求利息率i

这里的系数F不外乎是现值系数(如：复利现值系数PVIF年金现值系数PVIFA)和终值系数(如：复利终值系数FVIF、年金终值系数FVIFA)。 (一)已知的是现值系数 那么系数与利息率(也即贴现率)之间是反向关系：贴现率越大系数反而越小，可用图1表示。 图1中。F表示根据题意计算出来的年金现值系数(复利现值系数的图示略有不同，在于i可以等于0，此时纵轴上的系数F等于1)，F为在相应系数表中查到的略大于F的那个系数，F对应的利息率即为i。查表所得的另一个比F略小的系数记作F，其对应的利息率为i。

几种插值法的应用和比较

插值法的应用与比较 信科1302 万贤浩 13271038 1格朗日插值法 在数值分析中，拉格朗日插值法是以法国十八世纪数学家约瑟夫·路易斯·拉格朗日命名的一种多项式插值方法.许多实际问题中都用函数来表示某种内在联系或规律，而不少函数都只能通过实验和观测来了解.如对实践中的某个物理量进行观测，在若干个不同的地方得到相应的观测值，拉格朗日插值法可以找到一个多项式，其恰好在各个观测的点取到观测到的值.这样的多项式称为拉格朗日（插值）多项式.数学上来说，拉格朗日插值法可以给出一个恰好穿过二维平面上若干个已知点的多项式函数.拉格朗日插值法最早被英国数学家爱德华·华林于1779年发现，不久后由莱昂哈德·欧拉再次发现.1795年，拉格朗日在其著作《师范学校数学基础教程》中发表了这个插值方法，从此他的名字就和这个方法联系在一起. 1.1拉格朗日插值多项式 图1 已知平面上四个点：(?9, 5), (?4, 2), (?1, ?2), (7, 9)，拉格朗日多项式：)(x L （黑色）穿过所有点.而每个基本多项式：)(00x l y ,)(11x l y , )(22x l y 以及)(x l y ??各穿过对应的一点，并在其它的三个点的x 值上取零. 对于给定的若1+n 个点),(00y x ,),(11y x ,………),(n n y x ，对应于它们的次数不超过n 的拉格朗日多项式L 只有一个.如果计入次数更高的多项式，则有无穷个，因为所有与L 相差 ))((10x x x x --λ……)(n x x -的多项式都满足条件. 对某个多项式函数，已知有给定的1+k 个取值点： ),(00y x ,……,),(k k y x ,

几种常用的插值方法

数学系 信息与计算科学1班 李平 指导老师：唐振先 摘要:插值在诸如机械加工等工程技术和数据处理等科学研究中有许多直接的应用,在很多领域都要用插值的办法找出表格和中间值,插值还是数值积分微分方程数值解等数值计算的基础。本文归纳了几种常用的插值方法,并简单分析了其各自的优缺点。 关键词:任意阶多项式插值,分段多项式插值。 引言:所谓插值,通俗地说就是在若干以知的函数值之间插入一些未知函数值,而插值函数的类型最简单的选取是代数多项式。用多项式建立插值函数的方法主要用两种：一种是任意阶的插值多项式,它主要有三种基本的插值公式：单项式,拉格朗日和牛顿插值；另一种是分段多项式插值,它有Hermite 和spine 插值和分段线性插值。 一．任意阶多项式插值： 1.用单项式基本插值公式进行多项式插值： 多项式插值是求通过几个已知数据点的那个n-1阶多项式,即P n-1(X)=A 1+A 2X+…A n X n-1,它是一个单项式基本函数X 0,X 1…X n-1的集合来定义多项式,由已知n 个点（X,Y ）构成的集合,可以使多项式通过没数据点,并为n 个未知系数Ai 写出n 个方程,这n 个方程组成的方程组的系数矩阵为Vandermonde 矩阵。 虽然这个过程直观易懂,但它都不是建立插值多项式最好的办法,因为Vandermonde 方程组有可能是病态的,这样会导致单项式系数不确定。另外,单项式中的各项可能在大小上有很大的差异,这就导致了多项式计算中的舍入误差。 2.拉格朗日基本插值公式进行插值： 先构造一组插值函数L i （x ） =011011()()()() ()()()() i i n i i i i i i n x x x x x x x x x x x x x x x x -+-+--------，其中i=0，… n.容易看出n 次多项式L i （x ）满足L i （x ）=1，（i=j ）；L i （x ）=0，（i ≠j ），其中i=0，1…n ，令L i （x ）=0()n i i i y l x =∑这就是拉格朗日插值多项式。与单项式基本 函数插值多项式相比,拉格朗日插值有2个重要优点:首先,建立插值多项式不需要求解方程组；其次,它的估计值受舍入误差要小得多。拉格朗日插值公式结构

简单分类法及其应用一

物质的分类（第一课时）教案 一、教学目标 (一) 知识与技能 1、了解分类法在日常生活中应用的普遍性和重要性。 2、从物质的组成和性质对物质进行分类，为研究物质的通性建立框架，将知识系统化。 3、掌握“交叉分类法”、“树状分类法”。 （二）过程与方法 多角度、多标准对化学知识进行分类，体验分类的重要性。 （三）情感态度与价值观 1、形成将生产、生活实践与所学的化学知识相联系的意识。 2、体验分类在化学、各科学习上的重要性，将“分类思想”灌输于脑中，能够在后面学习中进行实际应用，培养及时分类总结的良好学习习惯。 二、教学重、难点 教学重点：了解常见化学物质及其变化的分类方法。 教学难点：用多种不同的方法对化学物质及其变化进行分类 三、教学过程 【讲述】请同学们把书拿出来，翻到课本24页，这节课我们学习第二章第一节“物质的分类”。 【板书】第一节物质的分类 【引入】 【讲述】在生活中，我们经常采用分类法，这样可以提高工作、学习的效率，使我们更快、更便捷地达到目的。 【提问】你们能找出分类在生活中的例子吗？ 【学生活动】在教师的引导下回答：（大型商场中的物品分类、图书馆里书籍的分类、网络中的信息分类、QQ好友的分类等）。 【过渡】举了这么多应用分类的例子，那么分类的概念是什么呢？请阅读课本第24页第一段，找出分类法的概念。 【板书】§2.1.1简单分类法及其应用 【板书】一、分类法：将大量事物按照事先设定的“标准”进行划分。 【强调】这里的“标准”加了双引号，表示强调，那究竟什么是标准呢？举个简单的例子，我们班一共有八十几个学生，根据是否住校，可分为走读生和住读生，“是否住校”就是分类的标准。 【讲述】在划分时我们只用了“是否住校”这一个标准，因此，我们称这种只采用一个标准分类的方法为“单一分类法”。 【板书】二、分类的方法 1、单一分类法（单分类） 【转折】单一分类法使用简单，但是，由于这种分类方法具有一定的局限性，它所能提供的信息较少，因此，我们有必要再学习一些其他的分类方法，以弥补单一分类方法的不足，首先我们来学习一下交叉分类法。 那么，究竟什么是交叉分类法？接下来，我通过一个具体的例子来给你们讲述一下。

空间插值

EX07：空间插值 本实验包含3个任务，任务1是进行趋势面分析（Trend surface analysis）；任务2使用IDW方法进行局部插值；任务3使用普通克里格（Ordinary kriging）方法进行插值。上述任务都可以在地统计分析（Geostatistical analyst）中进行空间插值，此时可以使用交叉有效性统计（如均方根统计）进行模型比较。地统计分析提供了比空间分析（Spatial Analyst）及ArcToolbox中插值工具更多信息及更好的用户界面。 任务1：趋势面模型用于插值 所需数据：stations.shp，包含Idaho州内及附近175个气象站的shapefile；idoutlgd，Idaho 州边界栅格文件。 在任务1中，在进行趋势面分析之前，首先查看stations.shp中的平均年度降水量数据。本任务中7、8、9等步骤涉及到栅格数据运算，为选作内容。 1.运行ArcCatalog，连接到EX07文件夹。运行ArcMap，将数据框架命名为Task1，将 stations.shp和idoutlgd添加到Task1。确保Geostatistical analyst和Spatial Analyst在Tools 菜单下的Extensions中的复选框被设置，且相应的工具条在程序中显示出来。 2.单击Geostatistical analyst中的下拉键头，指向Explorer Data，选择Trend Analysis。在 Trend Analysis对话框的底部，选择数据源的Layer为stations.shp，Attribute为ANN_PREC。 3.将Trend Analysis对话框最大化。对话框中的3D图表达了两种趋势信息：在YZ平面 中由北向南倾斜，在XZ平面中先表现为由西向东倾斜，而后些微上升。南北方向的趋势比东西方向趋势更为明显，即Idaho州降水量由北向南递减。关闭对话框。 4.单击Geostatistical analyst中的下拉键头，选择Geostatistical Wizard。在第1页中进行输 入数据和地统计方法的选择。单击Input Data下拉键头，选择stations。将Attribute选择为ANN_PREC。在Methods框架中，选择Global Polynomial Interpolation。 5.在下一页可以选择趋势面模型采用的阶数（Power）。在Power列表中提供了1-10的选 择。选择1作为阶数。下一页绘制了预测值与观测值、误差与观测值之间的分布图及一次趋势面模型相关统计。RMS是对趋势面模型综合符合度的一种衡量，在此起数值为 6.073。按Back返回且将阶数设置为2，此时RMS变为6.085。重复调整阶数，选择具 有最小RMS数值的趋势面模型即为本本任务最佳综合模型。对于ANN_PREC，最佳阶数设置为5。将阶数设置为5后单击Finish。在Output Layer Information对话框单击OK。Q1：当阶数为5时，RMS统计值是多少？ 6.Geostatistical analyst（GA）的输出为Global Polynomial Interpolation Prediction Map，与 stations具有相同的范围。在Global Polynomial Interpolation Prediction Map上单击右键选择Properties，在Symbology页包含4个显示选项：山体阴影（Hillshade）、等高线（Contours）、栅格（Grid）和填充等高线（Filled Contours），选择Filled Contours后单击分类（Classify）。在分类对话框中，选择手工分类，将其分为7类并将分类线设置为 10、15、20、25、30和35。单击OK关闭对话框。等高线（等雨量线）用不同色彩作 分类。 7.要将Global Polynomial Interpolation Prediction Map裁剪至与Idaho州边界相符，首先将 GA数据转化为栅格数据。在Global Polynomial Interpolation Prediction Map上单击右键，指向Data，选择Export to Raster，在弹出的对话框中，设置单元大小为200（米），并将输出命名为trend5_temp。单击OK进行数据输出。将trend5_temp添加到地图，检查trend5_temp中位于州边界外部的数值。