数学建模课后习题

第一章 课后习题6.

利用1.5节药物中毒施救模型确定对于孩子及成人服用氨茶碱能引起严重中毒和致命的最小剂量。

解：假设病人服用氨茶碱的总剂量为a ，由书中已建立的模型和假设得出肠胃中的药量为：

)()0(mg M x =

由于肠胃中药物向血液系统的转移率与药量)(t x 成正比，比例系数0>λ，得到微分方程

M x x dt

dx

=-=)0(,λ （1） 原模型已假设0=t 时血液中药量无药物，则0)0(=y ，)(t y 的增长速度为x λ。由于治疗而减少的速度与)(t y 本身成正比，比例系数0>μ，所以得到方程：

0)0(,=-=y y x dt

dy

μλ （2） 方程（1）可转换为：t

Me t x λ-=)(

带入方程（2）可得：)()(t t e e M t y λμμ

λλ

----=

将01386=λ和1155.0=μ带入以上两方程，得：

t Me t x 1386.0)(-= )(6)(13866.01155.0---=e e M t y t

针对孩子求解，得：

严重中毒时间及服用最小剂量：h t 876.7=，mg M 87.494=； 致命中毒时间及服用最小剂量：h t 876.7=，mg M 8.4694= 针对成人求解：

严重中毒时间及服用最小剂量：h t 876.7=，mg M 83.945= 致命时间及服用最小剂量：h t 876.7=，mg M 74.1987=

课后习题7.

对于1.5节的模型，如果采用的是体外血液透析的办法，求解药物中毒施救模型的血液用药量的变化并作图。

解：已知血液透析法是自身排除率的6倍，所以639.06==μu

t e t x λ-=1100)(，x 为胃肠道中的药量，1386.0=λ )(6600)(t t e e t y λμ---=

1386.0,639.0,5.236)2(,1100,2,====≥-=-λλλu z e x t uz x dt

dz

t 解得：()2,274.112275693.01386.0≥+=--t e e t z t t

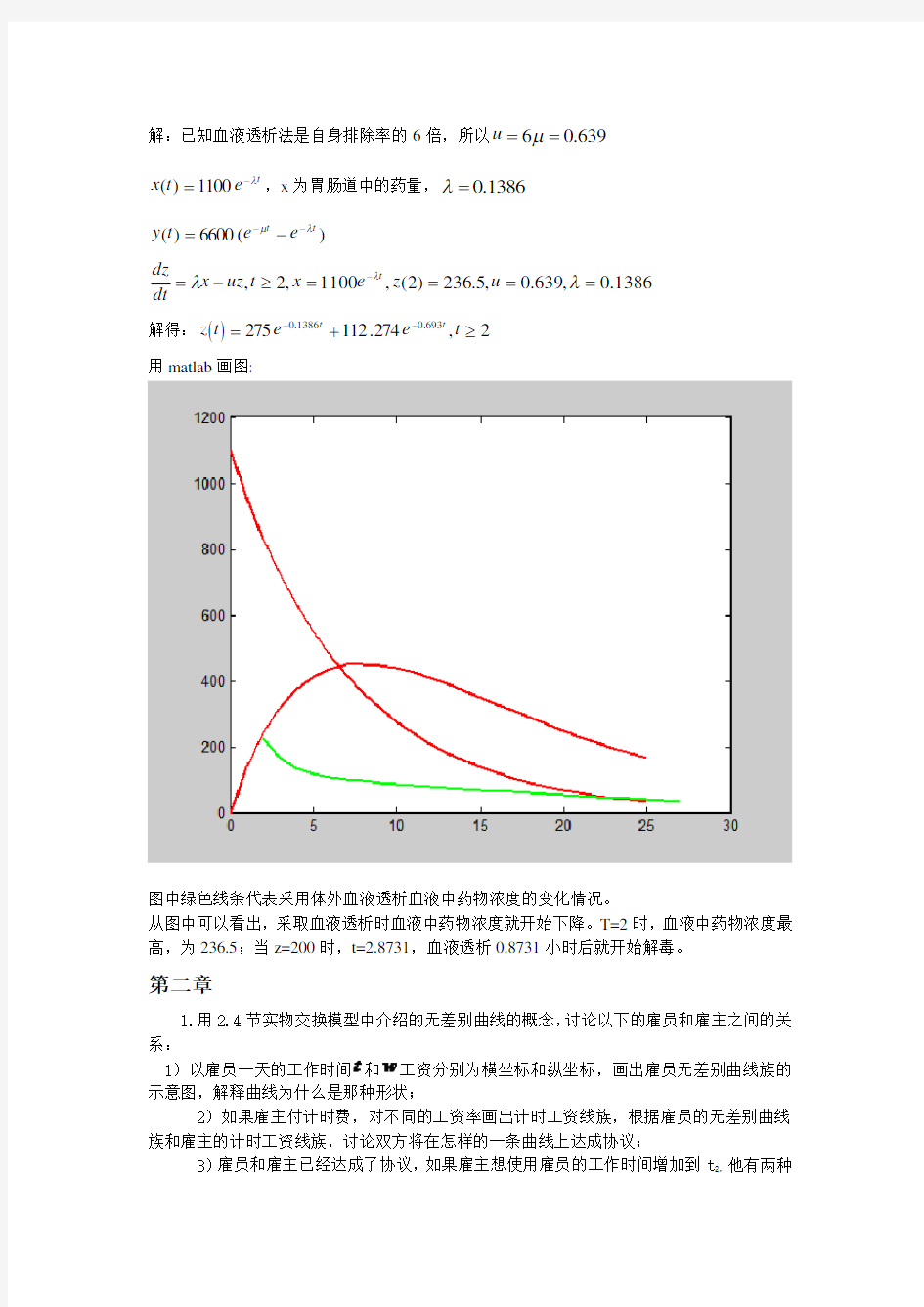
用matlab 画图:

图中绿色线条代表采用体外血液透析血液中药物浓度的变化情况。

从图中可以看出，采取血液透析时血液中药物浓度就开始下降。T=2时，血液中药物浓度最高，为236.5；当z=200时，t=2.8731，血液透析0.8731小时后就开始解毒。

第二章

1.用

2.4节实物交换模型中介绍的无差别曲线的概念，讨论以下的雇员和雇主之间的关系：

1）以雇员一天的工作时间和工资分别为横坐标和纵坐标，画出雇员无差别曲线族的示意图，解释曲线为什么是那种形状；

2）如果雇主付计时费，对不同的工资率画出计时工资线族，根据雇员的无差别曲线族和雇主的计时工资线族，讨论双方将在怎样的一条曲线上达成协议；

3）雇员和雇主已经达成了协议，如果雇主想使用雇员的工作时间增加到t 2，他有两种

办法：一是提高计时工资率，在协议线的另一点达成新的协议；二是实行超时工资

制，即对工时仍付原计时工资，对工时付给更高的超时工资，试用作图方法分析那种办法对雇主更有利，指出这个结果的条件。

解：

1）雇员的无差别曲线族是下凸的，如图。当工资较低时，他愿意以多的工作时间换取少的工资；当工资较高时，就要求以多的工资来增加工作时间。

2）雇主的计时工资族是，是工资率，这族直线与的切点，

等的连线为雇员与雇主的协议线，通常是上升的，见图：

3）设双方在点达成协议，当雇主想使雇员的工作时间增至时，用提高计时工资率的办法，应在协议线上找出横坐标为的点，工资额为，见上图，用

超时工资的办法，应从点作某一条无差别曲线的切线，使切点P2’的横坐标刚好是t2，若点P2’在P2的下方，则工资额w2’

课后第三章习题

1.在3.1节的存贮模型总费用中增加购买货物本身的费用，重新确定最优订货周期和订货批量，证明在不允许缺货模型和允许缺货模型中结果都与原来的一样。

解:

设购买单位重量货物的费用为k，对于不允许缺货模型，每天平均费用为

，T,Q的最优结果不变，对于允许缺货模型，每天平均费用为

，注意到，可知T，Q的最优结果也不变。

2.建立不允许缺货的生产销售存贮模型，设生产速率为常数k，销售速率为常数r，k>r，

在每个生产周期T内，开始的一段时间一边生产一边销售，后来的一段时间

只销售不生产，画出存贮量q(t)的图形，设每次生产准备费为c1,单位时间每件产品存贮费为c2，以总费用最小为目标确定最优生产周期，讨论和的情况。解:

贮存量q（t）的图形如图，单位时间总费用，，使c（T）达到最小值的最优周期。

当k>>r时，，相当于不考虑生产的情况，当时，，产量被销售量抵消，无法形成贮存量。

第四章

1、某银行经理计划用一笔资金进行有价证券的投资，可供购进的证券以及其信用等级，到期年限，收益如表所示。按照规定，市政证券的收益可以免税，其他证券的收益需按50%的税率纳税。此外还有以下限制:

（1）政府及代办机构的证券总共至少要购进400万元；

（2）所购证券的平均信用等级不超过1.4（信用等级数字越小，信用程度越高）；（3）所购证券的平均到期年限不超过5年。

表1 证券信息

问:（1）若该经理有1000万元资金，应如何投资？

（2）如果能够以2.75%的利率借到不超过100万元的资金，该经理应如何操作？（3）在1000万元资金情况下，若证券A的税前收益增加为4.5%，投资应否改变？若证券C的税前收益减少为4.8%，投资应否改变？

1.1 问题分析

问经理应该如何投资实际上是在问对已知的几种类型的证券要如何投资才能使得经理的最终收益最大。应该先对表中所给的几种证券的各个数据进行分析，列出几种证券投资后经理的收益函数，同时使得该函数所得结果要满足题目

中给定的几个限制。对于（2）、（3）问的求解只用调整相应的限制条件和第一问函数的几个三叔即可。 1.2 模型建立

（1)假设投资给证券A ，B ，C ，D ，E 的资金分别为a ，b ，c ，d ，e （百万元），经理最终的收益为y （百万元），则可以建立如下数学模型:

e *0.045d *0.022c *0.025b *0.027a *0.043y ++++=

??????

?≥≤+≤++≥++0

e d,c,b,a,0

e *3-d *2-c -b *10a *40e *36d *4-c *4-b *6a *64

d c b 用LINGO 软件求解：

得到如下结果：

证券A 投资2.182百万元，证券C 投资7.364百万元，证券E 投资0.454百万元；

经理最大税后收益为0.298百万元。

(2)由(1)的结果可知，若资金增加100万元，收益可增加0.0298百万元。大于以2.75%的利率借到100万元资金的利息，所以应借贷。修改（1）中的条件建立如下的心新模型：

e *0.045d *0.022c *0.025b *0.027a *0.043y ++++=

??????

?≥≤+≤++≥++0

e d,c,b,a,0

e *3-d *2-c -b *10a *411e *36d *4-c *4-b *6a *64

d c b

求解得到:

证券A投资2.40百万元，证券C投资8.10百万元，证券E投资0.50百万元，最大税后收益为0.3007百万元。

(3)由(1)的结果中目标函数系数的允许范围可知，证券A的税前收益可增加0.35%，故若证券A的税前收益增加为4.5%，投资不应改变；证券C的税前收益可减少0.112%(注意按50%的税率纳税)，故若证券C的税前收益减少为4.8%，投资应该改变。

2、一家出版社准备在某市建立两个销售代理点，向7个区的大学生售书，每个区的大学生数量（单位:千人）已经表示在图上。每个销售代理点只能向本区和相邻区的大学生售书，这两点销售代理点应建立在何处，才能使所能供应的大学生的数量最大？建立该问题的整数线性规划模型并求解。

图1

2.2 问题分析

首先简化作图，使得图中的邻里关系更加清楚，其次，通过假设0-1变量得到供应量最大化的函数，由于一个地区不能被两个销售点供应，所以得到七个限制条件，并由LINGO求解，得到一个0-1整数规划问题的解.

2.3 建立模型

将大学生数量为34，29，42，21，56，18，71的区分别编号为1，2，3，4，5，6，7区，如图所示：

记r i r 为第i 区的大学生人数，用0-1变量ij x =1表示(i,j)区的大学生由一个销售代理点供应图书(i

ij

j i j

i

x

r r ∑+相邻

,)(

2,≤∑j

i ij x

i x x j

ji j

ij ?≤+∑∑,1

{}1,0∈ij x

63x 12+76x 13+71x 23+50x 24+85x 25+63x 34+77x 45+39x 46+92x 47+74x 56+89x 67

x 12+x 13+x 23+x 24+x 25+x 34+x 45+x 46+x 47+x 56+x 67 2

x 12+x 13 1 x 12+x 23+x 24+x 25 1 x 13+x 23+x 24 1 x 24+x 34+x 45+x 46+x 47 1 x 25+x 45+x 56 1 x 46+x 56+x 67 1 x 47+x 67 1 x ij =0或1

用LINGO 软件求解：

得到最优解为x

25 = x

47

= 1,其余均为0，最优解为177人。

3、某储蓄所每天的营业时间是上午9:00到下午5:00。根据经验，每天不同时间段所需要的服务员数量如表所示：

储蓄所可以雇佣全时和半时两类服务员。全时服务员每天报酬100元，从上午9:00到下午5:00工作，但中午12:00到下午2:00之间必须安排1h的午餐时间。储蓄所每天可以雇佣不超过3名的半时服务员，每个半时服务员必须连续工作4h,报酬40元。问该储蓄所应如何雇佣全时和半时两类服务员？如果不能雇佣半时服务员，每天至少增加多少费用？如果该雇佣半时服务员的数量没有限制，每天可以减少多少费用？

3.2 问题分析

先为午餐时间的服务人员假定一个人数，再利用题目所给的表中的各个时段服务人员的相应限制人数来假定各个时段的无非人员人数。表中每个时段所需服务员人数可以得到若干个约束条件，目标函数即为服务员数与工资的乘积得出，最小值即为最优解。

若不能雇佣半时服务员，则使其数量为零并重新修改原模型；如果雇佣半时服务员的人数没有限制，则在原来模型的基础上去掉关于半时工作人员数量的约束条件即可得出新的模型。

3.3 模型建立

储蓄所每天雇佣的全时服务员中以12:00-1:00为午餐时间的有a名，以1:00-2:00为午餐时间的有b名；半时服务员中从9:00，10:00，11:00，12:00，1:00开始工作的分别为A,B,C,D,E名。

100*x+100*y+40*A+40*B+40*C+40*D+40*E;

x+y+A4;

x+y+A+B3;

x+y+A+B+C4;

y+A+B+C+D6;

x+B+C+D+E5;

x+y+C+D+E6;

x+y+D+E;

x+y+E8;

A+B+C+D+E3;

x,y,A,B,C,D,E0且为整数

求解:

得到最优解x=3,y=4,A=0,B=0,C=2,D=0,E=1,最小费用为820元。

如果不能雇佣半时服务员，则最优解x=5，y=6,A=0,B=0,C=0,D=0,E=0,最小费用为1100元，即每天至少增加1100-820=280元。

如果雇佣半时服务员的数量没有限制，则最优解为x=0,y=0,A=4,B=0,C=0,D=2,E=8，最小费用为560元，即每天可以减少费用820-560=260元。

马尔萨斯人口模型及阻滞增长模型

1.1 时间:1790年-2000年

绘图代码如下：

t=1790:10:2000;

x=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0 105.7 122.8 131.7 150.7 179.3 203.2 226.5 248.7 281.4];

p=polyfit(t,log(x),1);

r=p(1)

x0=exp(p(2))

x1=x0.*exp(r.*t);

plot(t,x,'r+',t,x1,'b') %红色的为原始数据，蓝色的为拟合数据

r=0.0202 ，x0=1.1960e-15

图型如下：

1.2 时间：1790年-1900年

绘图代码：

t=1790:10:1900;

x=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0];

p=polyfit(t,log(x),1);

r=p(1)

x0=exp(p(2))

x1=x0.*exp(r.*t);

plot(t,x,'r+',t,x1,'b') %红色的为原始数据，蓝色的为拟合数据

r=0.0274，x0=1.9790e-21

图像如下：

1、阻滞增长模型

clc;clear;

t = 1790:10:1900;

x=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0]; x_m = x(1,1:11);

y = ones(1,11);

for i=1:11

y(i) = (x(i+1)-x(i))/x(i)/10;

end

p = polyfit(x_m,y,1);

r = p(2);

xm = r/-p(1);

计算得到：r=0.208 ，xm = 151.1570；

绘制拟合曲线代码：

clear; clc;

format compact;

x=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0 105.7 122.8 131.7 150.7 179.3 203.2 226.5 248.7 281.4];

len=length(x);

t=0:len-1;

x0=3.9;r=0.2876;

xm=312.3413;

y=xm./(1+(xm/x0-1)*exp(-r*t));

plot(t,x,'r+',t,y,'b-');

拟合图像结果如下：

得到的人口数据如下：

由拟合图和所得数据可得看出，阻滞人口增长模型与实际人口的数量相符程度比马尔萨斯模型的符合程度高很多。

数学建模作业

数学建模作业 姓名:李成靖 学号:140803０3１１ 班级:计科1403班 日期:２０15．12。30

１.某班准备从5名游泳队员中选4人组成接力队，参加学校的4×100ｍ混合泳接力比赛,5名队员４种泳姿的百米平均成绩如下表所示，问应如何选拔队员组成接力队? 如果最近队员丁的蛙泳成绩有较大的退步，只有１′1５＂２;而队员戊经过艰苦训练自由泳成绩有所进步,达到57”5，组成接力队的方案是否应该调整? 名队员4种泳姿的百米平均成绩 ｉj 若参选择队员i 加泳姿j 的比赛，记x i ｊ＝1， 否则记ｘi ｊ=０ 目标函数： 即m ｉn=66．8*x11+7５.６*ｘ1２+87＊x13+58．６＊x1４+57。2＊x21＋66*x22+66.４＊x ２3＋53＊x2４＋７8＊ｘ3１+67．8＊x32+８4。6*ｘ３3+59．４*x34+70*x ４1+74。2＊x42+69.６*x ４３＋５７。2＊x44+6７。4＊ｘ5１+71＊ｘ5２＋8３。8*x53＋62.4*x5４; 约束条件: x 11＋x12+x13＋x14〈=1； x ２1＋x22+x2３+x ２4〈=1; x ３１+x32+x33+x34<＝1； x ４1+ｘ4２＋x ４3+x44〈＝１； x ５1＋ｘ５2+ｘ５３+ｘ54＜=1； ｘ11＋x ２1+ｘ31＋x41+x51=1； x １2+ｘ2２＋x32+x4２+ｘ５2=１; ｘ13+x ２3＋x33+x43+x53=１; ｘ14+ｘ24+x ３4＋ｘ4４+x54=１; 甲 乙 丙 丁 戊 蝶泳 1′06＂8 ５7”２ 1′1８” 1′１0” １′07＂４ 仰泳 1′１5＂6 1′06＂ 1′0７”8 １′14"２ 1′11＂ 蛙泳 1′２7” １′0６"4 1′２4"6 1′09＂6 １′2３"8 自由泳 5８"6 53” 59”４ 5７”２ 1′02”４ ∑∑=== 415 1j i ij ij x c Z Min

数学模型第三版课后习题答案.doc

《数学模型》作业解答 第七章（ 2008 年 12 月 4 日） 1．对于节蛛网模型讨论下列问题： （ 1）因为一个时段上市的商品不能立即售完，其数量也会影响到下一时段的价格，所以第 k 1时段的价格y k 1由第k 1 和第 k 时段的数量x k 1和x k决定，如果仍设x k 1仍只取

决于 y k ，给出稳定平衡的条件，并与节的结果进行比较 . （ 2）若除了 y k 1 由 x k 1 和 x k 决定之外， x k 1 也由前两个时段的价格 析稳定平衡的条件是否还会放宽 . 解：（ 1）由题设条件可得需求函数、供应函数分别为： y k 1 f x k 1 x k ) ( 2 x k 1 h( y k ) 在 P 0 (x 0 , y 0 ) 点附近用直线来近似曲线 f , h ，得到 y k 1 y 0 ( x k 1 x k x 0 ), 2 x k 1 x 0 ( y k y 0 ) , 由（ 2）得 x k 2 x 0 ( y k 1 y 0 ) （ 1）代入（ 3）得 x k 2 x 0 ( x k 1x k x 0 ) 2 2x k 2 x k 1 x k 2x 0 2 x 0 对应齐次方程的特征方程为 2 2 ( ) 2 8 特征根为 1, 2 4 y k 和 y k 1 确定 . 试分 (1) ( 2) (3) 当 8 时，则有特征根在单位圆外，设 8 ，则

1,2 ( ) 2 ( ) 2 8 42 2 4 1,2 1 2 即平衡稳定的条件为 2与 P 207 的结果一致 . （ 2）此时需求函数、供应函数在 P 0 (x 0 , y 0 ) 处附近的直线近似表达式分别为： y k 1 y 0 ( x k 1 x k x 0 ), ( 4) 2 x k 1 x 0 ( y k y k 1 y 0 ) , ( 5) 2 由（ 5）得， (x x 0 ) β(y y y k 1 y 0 ) ( 6 ) 2 k 3 k 2 将（ 4）代入（ 6），得 2( x k 3 x 0 ) ( x k 2 x k 1 x 0 ) ( x k 1 x k x 0 ) 2 2 4 x k 3x k 2 2 x k 1 x k 4 x 0 4 x 0 对应齐次方程的特征方程为 4 3 2 2 0 (7) 代数方程（ 7 ）无正实根，且 αβ , , 2 4 不是（ 7）的根 . 设（ 7）的三个非零根分 别为 1, 2, 3，则 1 2 3 4 1 2 2 3 3 1 2 1 2 3 4 对（ 7）作变换： , 则 12 3 q 0, p 其中 p 1 (2 2 2 ), q 1(833 2 2 ) 4 12 4 123 6

数学模型习题解答解读

上机练习题一 班级： 姓名： 学号： 1.建立起始值=3,增量值=5.5,终止值=44的一维数组x 答案： x=(3:5.5:44) 2.写出计算 Sin(30o )的程序语句. 答案： sin(pi*30/180) 或 sin(pi/6) 3.矩阵??????????=187624323A ,矩阵???? ??????=333222111B ;分别求出B A ?及A 与B 中对应元素之间的乘积. 答案：A = [3,2,3; 4,2,6; 7,8,1] B = [1,1,1; 2,2,2; 3,3,3] A*B ；A.*B 4计算行列式的值1 876243 23=A 。答案：det(A) 5对矩阵 ???? ??????=187624323A 进行下述操作。 (1)求秩。答案：rank(A) (2)求转置。答案：A' (3) 对矩阵求逆，求伪逆。答案：inv(A) ，pinv(A) (4) 左右反转,上下反转。答案：fliplr(A)，flipud(A) (5) 求矩阵的特征值. 答案：[u,v]=eig(A) (6) 取出上三角和下三角. 答案：triu(A) tril(A) (7)以A 为分块作一个3行2列的分块矩阵。答案：repmat(a) 6 计算矩阵??????????897473535与???? ??????638976242之和。 >> a=[5 3 5;3 7 4;7 9 8]; >> b=[2 4 2;6 7 9;8 3 6]; >> a+b 7 计算??????=572396a 与?? ????=864142b 的数组乘积。 >> a=[6 9 3;2 7 5]; >> b=[2 4 1;4 6 8];

数学建模练习题

数学建模试题 1、新工人的学习曲线 在电冰箱、电视机、汽车等行业中，装配工人的工作是一种重复性的熟练劳动。在这些行业中，新工人的学习过程如下：刚开始时由于技术不熟练，生产单位产品需要较多的劳动时间，随着不断的工作，新工人的熟练程度逐步提高，生产单位产品所需的劳动时间越来越短；当工人达到完全熟练程度以后，生产单位产品所需要的劳动时间就会稳定在一个定值。 纺织厂招收一批新工人学习1511型织布机的操作。观察工人的学习过程发现，当累计织完25匹布以后，工人织每匹布需要用16小时；当累计织完64匹布时，工人织每匹布用10小时.已知熟练工人织每匹布用8小时，是确定出新工人的学习曲线，并计算新工人用多少时间才能达到熟练工人的程度。 2、乙酸回收的最好效果 在,A B 两种物质的溶液中，我们想提取出物质A ，可以采取这样的方法：在,A B 的溶液中加入第三种物质C ，而C 与B 不互溶，利用A 在C 中的溶解度较大的特点，将A 提取出来。这种方法就是化工中的萃取过程。 现有稀水溶液的乙酸，利用苯作为溶剂，设苯的总体积为m 。进行3次萃取来回收乙酸.问每次应取多少苯量，方使从水溶液中萃取的乙酸最多？ 3、陈酒出售的最佳时机 某酒厂有批新酿的好酒，如果现在就出售，可得总收入050R =万元，如果窖 藏起来待来日（第n 年）按陈旧价格出售，第n 年末可得总收入为0R R =元。而银行利率为0.05r =。试分析这批好酒窖藏多少年后出售可使总收入的现值最大。 4、电子游戏中的数学 近年来，随着电子游戏的日益普及，电子游戏业已成为横跨信息技术和文化的重要产业。对电子游戏中的一些数学问题进行研究，成为数学界和相关人士的一个热门话题。 在某电子游戏中，玩家每次下注一元，由机器随机分配给玩家五张扑克牌，然后允许玩家有一次换牌的机会，即可以放弃其中的某几张牌，放弃的牌留下的空缺由机器在剩下的47张牌中再次随机分配。玩家的奖金依据其最后所持有的牌型而定。下面是一份典型的奖金分配表： 牌型 奖金（元） 同花大顺（10到A ） 800 同花顺 50 四张相同点数的牌 25 满堂红（三张同点加一对） 8 同花 5

数学建模作业43508

数学建模作业

1、在甲乙双方的一场战争中，部分甲方部队被乙方部队包围长达4个月，乙方封锁了所有 水陆交通通道，因此被包围的甲方只能依靠空中交通维持补给，运送4个月的供给依此分别 需要2次、3次、3次、4次飞行，每次飞行编队由50架飞机组成，每架飞机都需要3名飞 行员，每架飞机每月只能飞行一次，每名飞行员每月也只能飞行一次，每次执行完运输飞行 任务后的返回途中有20%的飞机被乙方部队击落，导致机上的飞行员也牺牲或失踪。在第 一个月开始时，甲方拥有110架飞机和330名熟练的飞行员，每个月开始时，甲方可以招聘 新飞行员和购买新飞机，新飞机必须经过一个月的检查磨合后才可以投入使用，新飞行员也 必须在熟练飞行员的指导下经过一个月的训练才能成为熟练飞行员而投入飞行（作为教练的 熟练飞行员本月不能参与飞行任务），每名熟练飞行员作为教练每月指导20名飞行员（包括 自己在内）进行训练，每名飞行员在完成本月的飞行任务后必须有一个月的带薪休假，然后 返回待命可再次投入飞行，已知各项费用平均单价如下表所示（单位：千元）。 第一个月第二个月第三个月第四个月新飞机价格200 195 190 185 闲置的熟练飞行员报酬7 6.9 6.8 6.7 10 9.9 9.8 9.7 教练及飞行员报酬和训练 费用 执行飞行任务的飞行员报 9 8.9 9.8 9.7 酬 休假期的飞行员报酬 5 4.9 4.8 4.7 （1）为甲方安排一个总费用最小的飞行计划。 （2）如果每名熟练飞行员作为教练每月指导不超过20名飞行员（包括自己在内）进行训练， 相应的模型和安排将会发生怎样的改变？ 解：（1） 设每月初购买飞机数量为d1，d2，d3,d4架，每月闲置飞机数量为 y1,y2,y3,y4架，每月教练与新飞行员总数量为a1,a2,a3,a4人，每月闲置熟练 飞行员的数量为b1,b2,b3,b4人。由于每月执行任务的飞行员和休假期的飞行员 的数量是固定的，即这部分的花费是固定的，所以在优化目标中可以不必考虑。 模型建立： 决策变量：设每月初购买飞机数量为d1，d2，d3,d4架，每月闲置飞机数量 为y1,y2,y3,y4架，每月教练与新飞行员总数量为a1,a2,a3,a4人，每月闲置熟 练飞行员的数量为b1,b2,b3,b4人。 目标函数：设总费用为z元，则由价格平均表可知： z=200d1+195d2+190d3+185d4+10a1+9.9a2+9.8a3+9.7a4+7b1+6.9b2+6.8b3+ 6.7b4 约束条件包括： （1）飞机数量限制：四个月中出去执行任务的飞机数量分别为100，150，150，200架次，每次安全返回的数量为80，120，120，160架次。 根据每个月的实际情况可得方程： 100+y1=110； 150+y2=80+y1+d1； 150+y3=120+y2+d2； 200+y4=120+y3+d3；

数学建模习题及答案课后习题

第一部分课后习题 1.学校共1000名学生，235人住在A宿舍，333人住在B宿舍，432人住在C宿舍。学生 们要组织一个10人的委员会，试用下列办法分配各宿舍的委员数： （1）按比例分配取整数的名额后，剩下的名额按惯例分给小数部分较大者。 （2）2.1节中的Q值方法。 （3）d’Hondt方法：将A，B，C各宿舍的人数用正整数n=1，2，3，…相除，其商数如 将所得商数从大到小取前10个（10为席位数），在数字下标以横线，表中A，B，C行有横线的数分别为2，3，5，这就是3个宿舍分配的席位。你能解释这种方法的道理吗。 如果委员会从10人增至15人，用以上3种方法再分配名额。将3种方法两次分配的结果列表比较。 （4）你能提出其他的方法吗。用你的方法分配上面的名额。 2.在超市购物时你注意到大包装商品比小包装商品便宜这种现象了吗。比如洁银牙膏50g 装的每支1.50元，120g装的3.00元，二者单位重量的价格比是1.2：1。试用比例方法构造模型解释这个现象。 （1）分析商品价格C与商品重量w的关系。价格由生产成本、包装成本和其他成本等决定，这些成本中有的与重量w成正比，有的与表面积成正比，还有与w无关的因素。 （2）给出单位重量价格c与w的关系，画出它的简图，说明w越大c越小，但是随着w 的增加c减少的程度变小。解释实际意义是什么。 3.一垂钓俱乐部鼓励垂钓者将调上的鱼放生，打算按照放生的鱼的重量给予奖励，俱乐部 只准备了一把软尺用于测量，请你设计按照测量的长度估计鱼的重量的方法。假定鱼池中只有一种鲈鱼，并且得到8条鱼的如下数据（胸围指鱼身的最大周长）： 先用机理分析建立模型，再用数据确定参数 4.用宽w的布条缠绕直径d的圆形管道，要求布条不重叠，问布条与管道轴线的夹角 应 多大（如图）。若知道管道长度，需用多长布条（可考虑两端的影响）。如果管道是其他形状呢。

数学模型课后答案

数学模型课后答案

《数学模型》作业答案 第二章(1)（2012年12月21日） 1．学校共1000名学生，235人住在A宿舍，333人住在B宿舍，432人住在C宿舍.学生们要组织一个10人的委员会，试用下列办法分配各宿舍的委员数： （1）. 按比例分配取整数的名额后,剩下的名额按惯例分给小数部分较大者; （2）. §1中的Q值方法； （3）.d’Hondt方法：将A、B、C各宿舍的人数用正整数n=1,2,3,……相除，其商数如下表：

将所得商数从大到小取前10个（10为席位数），在数字下标以横线，表中A 、B 、C 行有横线的数分别为2，3，5，这就是3个宿舍分配的席位.你能解释这种方法的道理吗？ 如果委员会从10个人增至15人，用以上3种方法再分配名额，将3种方法两次分配的结果列表比较. 解：先考虑N=10的分配方案， , 432 ,333 ,235321 ===p p p ∑==3 1 . 1000i i p 方法一（按比例分配） , 35.23 1 11 == ∑=i i p N p q , 33.33 1 22 == ∑=i i p N p q 32 .43 1 33 == ∑=i i p N p q 分配结果为： 4 ,3 ,3321 ===n n n 方法二（Q 值方法） 9个席位的分配结果（可用按比例分 配）为： 4 ,3 ,2321===n n n 第10个席位：计算Q 值为

2． 试用微积分方法，建立录像带记数器读数n 与转过时间的数学模型. 解： 设录像带记数器读数为n 时，录像带转过时间为t.其模型的假设见课本. 考虑t 到t t ?+时间内录像带缠绕在右轮盘上的长度，可得,2)(kdn wkn r vdt π+=两边积分，得 ??+=n t dn wkn r k vdt 0 )(2π ) 2 2 2 n wk k(r n πvt +=∴ . 2 2 2n v k w n v rk t ππ+=∴ 《数学模型》作业解答 第三章1（2008年10月14日） 1. 在 3.1节存贮模型的总费用中增加购买货物本身的费用,重新确定最优订货周期和订货批量．证明在不允许缺货模型中结果与原来的一样，而在允许缺货模型中最优订货周期和订货批量都比原来结果减少．

数学建模典型例题

一、人体重变化 某人的食量是10467焦/天，最基本新陈代谢要自动消耗其中的5038焦/天。每天的体育运动消耗热量大约是69焦/（千克?天）乘以他的体重（千克）。假设以脂肪形式贮存的热量100% 地有效，而1千克脂肪含热量41868焦。试研究此人体重随时间变化的规律。 一、问题分析 人体重W（t）随时间t变化是由于消耗量和吸收量的差值所引起的，假设人体重随时间的变化是连续变化过程，因此可以通过研究在△t时间内体重W的变化值列出微分方程。 二、模型假设 1、以脂肪形式贮存的热量100%有效 2、当补充能量多于消耗能量时，多余能量以脂肪形式贮存 3、假设体重的变化是一个连续函数 4、初始体重为W0 三、模型建立 假设在△t时间内： 体重的变化量为W（t+△t）-W(t)； 身体一天内的热量的剩余为（10467-5038-69*W（t）） 将其乘以△t即为一小段时间内剩下的热量； 转换成微分方程为：d[W(t+△t)-W(t)]=(10467-5038-69*W(t))dt； 四、模型求解 d(5429-69W)/(5429-69W)=-69dt/41686 W(0)=W0 解得： 5429-69W=（5429-69W0）e(-69t/41686) 即： W（t）=5429/69-（5429-69W0）/5429e(-69t/41686) 当t趋于无穷时，w=81; 二、投资策略模型 一、问题重述 一家公司要投资一个车队并尝试着决定保留汽车时间的最佳方案。5年后，它将卖出所有剩余汽车并让一家外围公司提供运输。在策划下一个5年计划时，这家公司评估在年i 的开始买进汽车并在年j的开始卖出汽车，将有净成本a ij（购入价减去折旧加上运营和维修成本）ij

数学模型课后答案

《数学模型》作业答案 第二章(1)（2012年12月21日） 1． 学校共1000名学生，235人住在A 宿舍，333人住在B 宿舍，432人住在C 宿舍.学生们 要组织一个10人的委员会，试用下列办法分配各宿舍的委员数： （1）. 按比例分配取整数的名额后,剩下的名额按惯例分给小数部分较大者; （2）. §1中的Q 值方法； （3）.d ’Hondt 方法：将A 、B 、C 各宿舍的人数用正整数n=1,2,3,……相除，其商数如下表： 将所得商数从大到小取前10个（10为席位数），在数字下标以横线，表中A 、B 、C 行有横线的数分别为2，3，5，这就是3个宿舍分配的席位.你能解释这种方法的道理吗？ 如果委员会从10个人增至15人，用以上3种方法再分配名额，将3种方法两次分配的结果列表比较. 解：先考虑N=10的分配方案， ,432 ,333 ,235321===p p p ∑==3 1 .1000i i p 方法一（按比例分配） ,35.23 1 11== ∑=i i p N p q ,33.33 1 22== ∑=i i p N p q 32.43 1 33== ∑=i i p N p q 分配结果为： 4 ,3 ,3321===n n n 方法二（Q 值方法） 9个席位的分配结果（可用按比例分配）为： 4 ,3 ,2321===n n n

第10个席位：计算Q 值为 ,17.92043223521=?=Q ,75.92404333322=?=Q 2.9331544322 3=?=Q 3Q 最大，第10个席位应给C.分配结果为 5 ,3 ,2321===n n n 方法三（d ’Hondt 方法） 此方法的分配结果为：5 ,3 ,2321===n n n 此方法的道理是：记i p 和i n 为各宿舍的人数和席位（i=1,2,3代表A 、B 、C 宿舍）. i i n p 是每席位代表的人数，取,,2,1 =i n 从而得到的i i n p 中选较大者，可使对所有的,i i i n p 尽量接近. 再考虑15=N 的分配方案，类似地可得名额分配结果.现将3种方法两次分配的结果列表如下： 2． 试用微积分方法，建立录像带记数器读数n 与转过时间的数学模型. 解： 设录像带记数器读数为n 时，录像带转过时间为t.其模型的假设见课本. 考虑t 到t t ?+时间内录像带缠绕在右轮盘上的长度，可得,2)(kdn wkn r vdt π+=两边积分，得 ?? +=n t dn wkn r k vdt 0 )(2π )22 2 n wk k(r n πvt +=∴ .2 22n v k w n v rk t ππ+=∴ 《数学模型》作业解答 第三章1（2008年10月14日）

数学建模习题

4 美术馆悬挂着一副高h 的画，画的下边比一个观众的眼睛高d ，这个观众站在距离墙多 远的距离才是最佳视角？ 假设：人与墙的距离为x x d = αtan x h d += +)tan(βα ))tan((tan αβαβ-+= α βαα βαt a n )t a n (1t a n )t a n (?++-+= x h d x d x h +?+= 1 x h d d x h )(+?+ = ∵ab b a 2≥+ 当b a =时 ab b a 2=+ ∴) (2tan h d d h +?= β

8. 细菌生长繁殖速度之快、以及数量之大是难以琢磨的．而有些细菌是有益的、更多 的是疾病之源．下面记录了某种细菌的繁殖数据，研究： （1）开始时细菌的个数是多少？ （2）如果细菌以过去的速度继续增长，一个月后细菌的个数是多少？ 细菌繁殖过程记录数据表1-2 假设：（1），一个月是30天，天数为x，开始时细菌的个数为k。 （2），细菌的生长环境（包括温度，湿度，空气含量等）保持不变；细菌在生长过程中没有大量死亡的特殊情况； x （1） y* e k 由上表公式得出开始时细菌的个数约是401个 带入公式（1）算出一个月后细菌的个数：

30 0.1969456 * y 401.573190 * 82 e 得出一个月后细菌的个数约是65266个。

2． 在超市购物时你注意到大包装商品比小包装商品便宜这种想象了吗.比如洁银牙膏50克装的每支1.50元,120克装的每支3.00元,二者单位的重量的价格比是1.2:1,试用比例方法构造模型解释这个现象. （1）分析商品的价格C 与商品重量W 的关系.价格由生产成本、包装成本和其它成本等决定，这些成本中有的与重量W 成正比，有的与表面积成正比，还有与W 无关的因素。 (2)给出单位重量价格C 与W 的关系。画出它的简图，说明W 越大C 越小，但是随着W 的增加C 减小的程度变小。解释实际意义是什么。 （1） 假设：商品几何相似相对长度为L ，质量为W ，体积为V ，表面积为S 。 因为：生产成本与重量W 成正比，与体积V 成正比，与长度3 L 成正比。 包装成本与表面积S 成正比，与长度2 L 成正比，与体积32V 成正比，与重量3 2W 成正比。 所以：33 221k w k w k C ++= 又∵w C c = ∴133 121--++=w k w k k c ( 321,,k k k 为大于零的常数) （2） 单位重量价格： w c C = ∵ 2 334 23 1----='w k w k c ＞0 3337 229 4 --+=''w k w k c ＞0 ∴图像为单调递减且上凹。

数学建模习题指导

数学建模习题指导 第一章 初等模型 讨论与思考 讨论题1 大小包装问题 在超市购物时你注意到大包装商品比小包装商品便宜这种现象吗？比如洁银牙膏50g 装的每支1.50元，120g 装的每支3.00元，二者单位重量的价格比是1.2:1，试用比例方法构造模型解释这种现象。 （1）分析商品价格C 与商品重量w 的关系。 （2）给出单位重量价格c 与w 的关系，并解释其实际意义。 提示： 决定商品价格的主要因素：生产成本、包装成本、其他成本。 单价随重量增加而减少 单价的减少随重量增加逐渐降低 思考题2 划艇比赛的成绩 赛艇是一种靠浆手划桨前进的小船，分单人艇、双人艇、四人艇、八人艇四种。各种艇虽大小不同，但形状相似。T.A.McMahon 比较了各种赛艇1964—1970年四次2000m 比赛的最好成绩(包括1964年和1968年两次奥运会和两次世界锦标赛)，见下表。建立数学模型解释比赛成绩与浆手数量之间的关系。 各种艇的比赛成绩与规格 γβα++=3 2w w C w w c γβα++=-3 123 431w w c γβ--='-3 2943 4w w c γβ+=''-

第二章 线性代数模型 森林管理问题 森林中的树木每年都要有一批砍伐出售。为了使这片森林不被耗尽且每年都有所收获，每当砍伐一棵树时，应该就地补种一棵幼苗，使森林树木的总数保持不变。被出售的树木，其价值取决于树木的高度。开始时森林中的树木有着不同的高度。我们希望能找到一个方案，在维持收获的前提下，如何砍伐树木，才能使被砍伐的树木获得最大的经济价值。 思考： 试解释为什么模型中求解得到的 为每周平均销售量会略小于模型假设中给出的1。 练习： 将钢琴销售的存贮策略修改为：当周末库存量为0或1时订购，使下周初的库存 达到3架；否则，不订购。建立马氏链模型，计算稳态下失去销售机会的概率和每周的平均销售量。 2.将钢琴销售的存贮策略修改为：当周末库存量为0时订购本周销售量加2架；否则，不订购。建立马氏链模型，计算稳态下失去销售机会的概率和每周的平均销售量。 第三章 优化模型 讨论题 1）最优下料问题 用已知尺寸的矩形板材加工半径一定的圆盘。给出几种加工排列方法，比较出最优下料方案。 2）广告促销竞争问题 甲乙两公司通过广告竞争销售商品，广告费分别为 x 和 y 。设甲乙公司商品的售量在两公司总售量中所占份额是它们的广告费在总广告费中所占份额的函数 又设公司的收入与售量成正比，从收入中扣除广告费后即为公司的利润。试构造模型的图形，并讨论甲公司怎样确定广告费才能使利润最大。 （1）令 （2）写出甲公司的利润表达式 对一定的 y ，使 p (x ) 最大的 x 的最优值应满足什么关系。用图解法确定这个最优值。 练习1 三个家具商店购买办公桌：A 需要30张，B 需要50张，C 需要45张。这些办公桌由两个工厂供应：工厂1生产70张，工厂2生产80张。下表给出了工厂和商店的距离（单位公里） ， 857.0=n R ) (),(y x y f y x x f ++的示意图。。画出则)()()(,t f t f t f y x x t 11=-++= 。 )(t p

数学建模课后习题答案

第一章 课后习题6. 利用1.5节药物中毒施救模型确定对于孩子及成人服用氨茶碱能引起严重中毒和致命的最小剂量。 解：假设病人服用氨茶碱的总剂量为a ，由书中已建立的模型和假设得出肠胃中的药量为： )()0(mg M x = 由于肠胃中药物向血液系统的转移率与药量)(t x 成正比，比例系数0>λ，得到微分方程 M x x dt dx =-=)0(,λ（1） 原模型已假设0=t 时血液中药量无药物，则0)0(=y ，)(t y 的增长速度为x λ。由于治疗而减少的速度与)(t y 本身成正比，比例系数0>μ，所以得到方程： 0)0(,=-=y y x dt dy μλ（2） 方程（1）可转换为：t Me t x λ-=)( 带入方程（2）可得：)()(t t e e M t y λμμ λλ ----= 将01386=λ和1155.0=μ带入以上两方程，得： t Me t x 1386.0)(-= )(6)(13866.01155.0---=e e M t y t 针对孩子求解，得： 严重中毒时间及服用最小剂量：h t 876.7=，mg M 87.494=； 致命中毒时间及服用最小剂量：h t 876.7=，mg M 8.4694= 针对成人求解： 严重中毒时间及服用最小剂量：h t 876.7=，mg M 83.945= 致命时间及服用最小剂量：h t 876.7=，mg M 74.1987= 课后习题7. 对于1.5节的模型，如果采用的是体外血液透析的办法，求解药物中毒施救模型的血液用药量的变化并作图。

解：已知血液透析法是自身排除率的6倍，所以639.06==μu t e t x λ-=1100)(，x 为胃肠道中的药量，1386.0=λ )(6600)(t t e e t y λμ---= 1386.0,639.0,5.236)2(,1100,2,====≥-=-λλλu z e x t uz x dt dz t 解得：()2,274.112275693.01386.0≥+=--t e e t z t t 用matlab 画图: 图中绿色线条代表采用体外血液透析血液中药物浓度的变化情况。 从图中可以看出，采取血液透析时血液中药物浓度就开始下降。T=2时，血液中药物浓度最高，为236.5；当z=200时，t=2.8731，血液透析0.8731小时后就开始解毒。 第二章 1.用 2.4节实物交换模型中介绍的无差别曲线的概念，讨论以下的雇员和雇主之间的关系： 1）以雇员一天的工作时间和工资分别为横坐标和纵坐标，画出雇员无差别曲线族的示意图，解释曲线为什么是那种形状； 2）如果雇主付计时费，对不同的工资率画出计时工资线族，根据雇员的无差别曲线族和雇主的计时工资线族，讨论双方将在怎样的一条曲线上达成协议； 3）雇员和雇主已经达成了协议，如果雇主想使用雇员的工作时间增加到t 2，他有两种

(完整版)数学模型第二章习题答案

15．速度为v 的风吹在迎风面积为s 的风车上，空气密度是ρ ，用量纲分析方法确定风车获得的功率P 与v 、S 、ρ的关系. 解: 设P 、v 、S 、ρ的关系为0),,,(=ρs v P f ， 其量纲表达式为: [P]=32-T ML , [v ]=1-LT ,[s ]=2L ,[ρ]=3-ML ,这里T M L ,,是基本量纲. 量纲矩阵为： A=) ??????? ???---ρ()() ()()()()(001310013212s v P T M L 齐次线性方程组为： ?? ? ??=--=+=-++0 30 32221414321y y y y y y y y 它的基本解为)1,1,3,1(-=y 由量纲i P 定理得 1131ρπs v P -=， 1 13ρλs v P =∴ ， 其中λ是无量纲常数. 16．雨滴的速度v 与空气密度ρ、粘滞系数μ和重力加速度g 有关，其中粘滞系数的定义是：运动物体在流体中受的摩擦力与速度梯度和接触面积的乘积成正比，比例系数为粘滞系 数，用量纲分析方法给出速度v 的表达式. 解：设v ,ρ,μ,g 的关系为(f v ,ρ,μ,g )=0.其量纲表达式为[v ]=LM 0T -1，[ρ]=L -3MT 0 ， [μ]=MLT -2 （LT -1L -1 ）-1L -2 =MLL -2T -2 T=L -1 MT -1 ，[g ]=LM 0T -2 ,其中L ，M ，T 是基本量纲. 量纲矩阵为 A=) ()()()()()() (210101101131g v T M L μρ??????????----- 齐次线性方程组Ay=0 ，即 ??? ??==+=+0 2y -y - y -0 y y 0y y -3y -y 431 324321 的基本解为y=(-3 ,-1 ,1 ,1) 由量纲i P 定理 得 g v μρπ1 3 --=. 3 ρ μλg v =∴，其中λ是无量纲常数.

数学建模习题

数学建模与数学实验课程练习 练习集锦 1简述数学建模的一般过程及建模过程中需要注意的问题。 2 简述数学模型及数学建模的特点。 3 简述数学建模的常用分类方法。 4求方程 06 /12 625 .05 .04 )(=------=x x x x f 的模最大的根的近似 值（精确到小数点后两位）。 5在抢渡长江模型中，如果水流速度 1.8/v m s =为常数，人的游泳速度 1.5/u m s =为常数，江面宽度为1200H m =，终点位置在起点下游 1000L m =处的条件，确定游泳者的最佳游泳路径及最短游泳时间。 6沿江的某一侧区域将建两个水厂，在江边建一个取水口。现需要设计最优的管线铺设方案，通过管线从取水口向水厂送水。水厂与江岸的位置见右图。 如果不用共用管线，城区单位建设费用是郊区的2倍。 （1） 对于最优方案，用α表示,βγ。 （2） 求最优取 水口位置。 7在层次分析法建模中，我们介绍了成对比较矩阵概念，已知矩阵P 是成对比较矩阵 (,0) P x

31/52a b P c d e f ?? ??=?? ???? ， （1）确定矩阵P 的未知元素。 （2）求P 模最大特征值。 （3）分析矩阵P 的一致性是否可以接受（随机一致性指标ＲＩ取）。 8在层次分析法建模中，我们介绍了成对比较矩阵概念，已知矩阵P 是三阶成对比较矩阵 322P ? ???=?????? ，（1）将矩阵P 元素补全。 （2）求P 模最 大特征值。 （3）分析矩阵P 的一致性是否可以接受（随机一致性指标ＲＩ取）。 9考虑下表数据 (1)用曲改直的思想确定经验公式形式。 （2）用最小二乘法确定经验公式系数。 10考虑微分方程

数学建模课后答案

第一章 4.在1、3节“椅子能在不平的地面上放稳不”的假设条件中,将四脚的连线呈正方形改为长方形,其余不变。试构造模型并求解。 答:相邻两椅脚与地面距离之与分别定义为)()(a g a f 和。f 与g 都就是连续函数。椅子在任何位置至少有三只脚着地,所以对于任意的a ,)()(a g a f 和中至少有一个不为零。不妨设0)0(,0)0(g >=f 。当椅子旋转90°后,对角线互换,0π/2)(,0)π/2(>=g f 。这样,改变椅子的位置使四只脚同时着地。就归结为证明如下的数学命题: 已 知 a a g a f 是和)()(的连续函数,对任意 0)π/2()0(,0)()(,===?f g a g a f a 且,0)π/2(,0)0(>>g f 。证明存在0a ,使0)()(00==a g a f 证:令0)π/2(0)0(),()()(<>-=h h a g a f a h 和则, 由g f 和的连续性知h 也就是连续函数。 根据连续函数的基本性质, 必存在0a (0＜0a ＜π/2)使0)(0=a h ,即0)()(00==a g a f 因为0)()(00=?a g a f ,所以0)()(00==a g a f

8 第二章

10.用已知尺寸的矩形板材加工半径一定的圆盘,给出几种简便有效的排列方法,使加工出尽可能多的圆盘。

第三章 5.根据最优定价模型 考虑成本随着销售量的增加而减少,则设 kx q x q -=0)( (1)k 就是产量增加一个单位时成本的降低 , 销售量x 与价格p 呈线性关系0,,>-=b a bp a x (2) 收入等于销售量乘以价格p :px x f =)( (3) 利润)()()(x q x f x r -= (4) 将(1)(2)(3)代入(4)求出 ka q kbp pa bp x r --++-=02)( 当k q b a ,,,0给定后容易求出使利润达到最大的定价*p 为 b a kb ka q p 2220*+--=

数学建模 练习题1

2.14成绩与体重数学建模 一、问题 举重比赛按照体育运动员的体重分组，你能在一些合理、简单的假设下，建立比赛成绩与体重之间的关系吗？下面是下一届奥运会的成绩，可供检验你的模型。 一、问题分析 成绩与肌肉的力度有直接关系，随着力度的增加，成绩呈上升趋势。 假设力度与肌肉横截面积成正比，而截面积和体重都与身体的某个特征尺寸有直接关联。由此可以找到成绩和体重之间的关系。可以以此建立模型。

二、模型假设以及符号说明 1．本模型主要考虑运动员举重总成绩和体重的关系，所以假设运动员其他条件相差不大。 2．运动员的举重能力用其举重的总成绩来刻画 3．符号说明： 人的体重 W 人的身高 h 肌肉横截面积 S 人的体积 V 肌肉强度 T 举重成绩 C 非肌肉重量 W1 斜率 K 三、模型构成 模型一 1．题中给出举重比赛按照体育运动员的体重分组，所以我们猜测成绩与体重应该是正比关系。 2．画出坐标图，体重越重，成绩越好，进一步验证了正比关系。 最大体重

从上图可以看出，体重越大，举重总成绩相对越好，所以我们猜测举重总成绩与体重大概成线性关系。则，我们可以用一次函数C=kW+b对三个体重进行拟合，根据图中数据，可得： = = 2.66， = = 1.45, = = 1.17 把b代入得出三个一次函数为： = 2.66W+143.8, = 1.45W+75.1, = 1.17W+69.7, 用上述模型计算得到的理论值,并画出图表与原图表进行比较： 最大体重

通过比较两个图表，我们可以推测体重与成绩数据的推测图表和已知图标的拟合度并不是特别的理想，所以我们可以认为用线性函数对举重总成绩与体重进行拟合的模型过于简单、粗略，考虑的因素比较少。 模型二 我们这一次综合各种因素来进行分析建模。 通过查阅各种自然科学磁疗，我们可以近似以为：一般举重运动员的举重能力是用举重成绩来衡量，而举重运动员的举重能力与其肌肉强度近似成正比关系，从而举重运动员的举重总成绩与其肌肉强度近似成正比，即： C = T (为常数且>0) ○1从运动生理学得知，肌肉的强度与其横截面积近似成正比，即： T = S (为常数且>0) ○ 2综合○1，○2可得 C=T=S ○3通过查阅资料，我们可以假设肌肉的横截面积正比于身高的平方，人的体重正比于身高的三次方，即可得： S = , W = (，为常数且>0，>0) 综合上述所有算式，我们有： C= S = ○ 4 因为W = ，我们可以推测出举重运动员举重总成绩与其体重的关系为： C = 利用题目表格中所给的体重和举重总成绩数据，求出上述模型的常数M。利用题目表格中所给的体重和举重总成绩数据，运用最小二乘法求出上述模型的系数 K 。因为体重超过108千克的运动员的体重没有具体的数据，为了模型的准确性，故将这个数据舍去。经过代入9次运算得出平均常数，为=20.3,=9.6，=9.0。于是举重运动员的举重总成绩与体重的关系模型为

数学建模习题答案

数学建模部分课后习题解答 中国地质大学 能源学院 华文静 1、在稳定的椅子问题中,如设椅子的四脚连线呈长方形,结论如何？ 解: 模型假设 （1） 椅子四条腿一样长,椅脚与地面接触处视为一点,四脚的连线呈长方形 （2） 地面高度就是连续变化的,沿任何方向都不会出现间断(没有像台阶那样的情 况),即从数学角度来瞧,地面就是连续曲面。这个假设相当于给出了椅子能放稳的必要条件 （3） 椅子在任何位置至少有三只脚同时着地。为了保证这一点,要求对于椅脚的间距 与椅腿的长度而言,地面就是相对平坦的。因为在地面上椅脚间距与椅腿长度的尺寸大小相当的范围内,如果出现深沟或凸峰(即使就是连续变化的),此时三只脚就是无法同时着地的。 模型建立 在上述假设下,解决问题的关键在于选择合适的变量,把椅子四只脚同时着地表示出来。首先,引入合适的变量来表示椅子位置的挪动。生活经验告诉我们,要把椅子通过挪动放稳,通常有拖动或转动椅子两种办法,也就就是数学上所说的平移与旋转变换。然而,平移椅子后问题的条件没有发生本质变化,所以用平移的办法就是不能解决问题的。于就是可尝试将椅子就地旋转,并试图在旋转过程中找到一种椅子能放稳的情形。 注意到椅脚连线呈长方形,长方形就是中心对称图形,绕它的对称中心旋转180度后,椅子仍在原地。把长方形绕它的对称中心旋转,这可以表示椅子位置的改变。于就是,旋转角度θ这一变量就表示了椅子的位置。为此,在平面上建立直角坐标系来解决问题。 设椅脚连线为长方形ABCD,以对角线AC 所在的直线为x 轴,对称中心O 为原点,建立平面直角坐标系。椅子绕O 点沿逆时针方向旋转角度θ后,长方形ABCD 转至A1B1C1D1的位置,这样就可以用旋转角）0（πθθ≤≤表示出椅子绕点O 旋转θ后的位置。 其次,把椅脚就是否着地用数学形式表示出来。当椅脚与地面的竖直距离为零时,椅脚就着地了,而当这个距离大于零时,椅脚不着地。由于椅子在不同的位置就是θ的函数,因此,椅脚与地面的竖直距离也就是θ的函数。 由于椅子有四只脚,因而椅脚与地面的竖直距离有四个,它们都就是θ的函数,而由假设(3)可知,椅子在任何位置至少有三只脚同时着地,即这四个函数对于任意的θ,其函数值至少有三个同时为0。因此,只需引入两个距离函数即可。考虑到长方形ABCD 就是对称中心图形,绕其对称中心O 沿逆时针方向旋转180度后,长方形位置不变,但A,C 与B,D 对换了。因此,记A,B 两脚与地面竖直距离之与为)(θf ,C,D 两脚之与为)(θg ,其中[] πθ，0∈,使得)()(00θθg f =成立。 模型求解 如果0)0()0(== g f ,那么结论成立。 如果)0(与) 0(g f 不同时为零,不妨设.0)0(,0)0(=>g f 这时,将长方形ABCD 绕点O

数学模型(第四版)课后详细答案

数学模型作业 六道题 作业一 1.P56.8一垂钓俱乐部鼓励垂钓者将钓上的鱼放生，打算按照放生的鱼的重量给予奖励，俱乐部只准备了一把软尺用于测量，请你设计按照测量的长度估计鱼的重量的方法。假定鱼池中只有一种鲈鱼，并且得到8条鱼的如下数据（胸围指鱼身的最大周长）： 解： 要求鱼的体重，我们利用质量计算公式：M=ρV。我们假定鱼池中是同一种鱼，于是可以近似地考虑其密度是相同的。至于鱼的体积问题，由于是同一种类，可以假定这种鱼在体型上是一致的。我们假设鱼的体积和鱼身长的立方成正比。即：V=k 1 L3，因此，模型为： 33 111 M V k l K L ρρ ===……………………………模型一 利用Eviews软件，用最小二乘法估计模型中的参数K 1 ，如下图1所示： 图1 从图1结果可以得到参数K 1 =0.014591，所以模型为： 3 1 M0.014591 L = 上述模型存在缺陷，因为它把肥鱼和瘦鱼同等看待。因此，有必要改进模型。如果只假定鱼的横截面是相似的，假设横截面积与鱼身最大周长的平方成 正比，即：V=k 2 d2L，因此，模型为： 身长 /cm 36.8 31.8 43.8 36.8 32.1 45.1 35.9 32.1 质量 /g 765 482 1162 737 482 1389 652 454 胸围 /cm 24.8 21.3 27.9 24.8 21.6 31.8 22.9 21.6

22222M V k d K d L L ρρ===……………………………… 模型二 利用Eviews 软件，用最小二乘法估计模型中的参数K 2，如下图2所示： 图2 从图2可以得到参数K 2=0. 032248，所以模型为： 22M 0.032248d L = 将实际数据与模型结果比较如表1所示： 实际数 据M 765 482 1162 737 482 1389 652 454 模型一M 1 727.165 469.214 1226.061 727.165 482.629 1338.502 675.108 482.619 模型二M 2 729.877 465.248 1099.465 729.877 482.960 1470.719 607.106 483.960 2.P131.2 一家出版社准备在某市建立两个销售代理点，向7个区的大学生售书，每个区的大学生数量（单位：千人）已经表示在图上。每个销售代理点只能向本区和一个相邻区的大学生售书，这两个代理点应该建在何处，才能使所能供应的大学生的数量最大？建立该问题的整数线性规划模型并求解。 解： 将大学生数量为34、29、42、21、56、18、71的区分别标号为1、2、3、4、5、6、7区，画出如下区域区之间的相邻关系： 2 5