
网课:二次函数中特殊四边形的存在性问题
学习目标:
1、通过二次函数中的特殊四边形存在性问题的探究、学习,获取解决这类问题的基本方法;经历解决二次函数中的特殊四边形存在性问题的探索过程,培养学生的理解能力,抽象能力,能正确认识问题的本质,提高知识迁移能力,积累解决问题的经验,感受数学知识对解决问题的价值;
2、通过函数中的特殊四边形存在性问题的解决,渗透“转化”、“分类”、“方程”、“数形结合”等数学思想,并在问题解决中体验成功的快乐,感受数学的魅力.
学习重点:利用“特殊四边形的性质”,或者“点在函数上”来建立等量关系,解决“点是否存在的问题”.
学习难点:从复杂的函数背景中提炼问题的本质,利用“特殊四边形的性质”,或者“点在函数上”来建立等量关系,解决“点是否存在的问题”.
背景问题:
如图,抛物线中,点A在x轴的正半轴上,点C在y轴的正半轴上,
OC=3,点D是直线AC与抛物线的交点。
问题一:在平面内是否存在一点B,使得以A、B、O、D为顶点的
四边形是平行四边形?
若存在,请直接写出B点的坐标;若不存在,请说明理由。
归纳:_________________________________________________
问题二:若点M在抛物线上,点N在x轴上,是否存在以A、D、M、N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由;
(备图1)(备图2)
归纳:
_____________________________________________________________________________
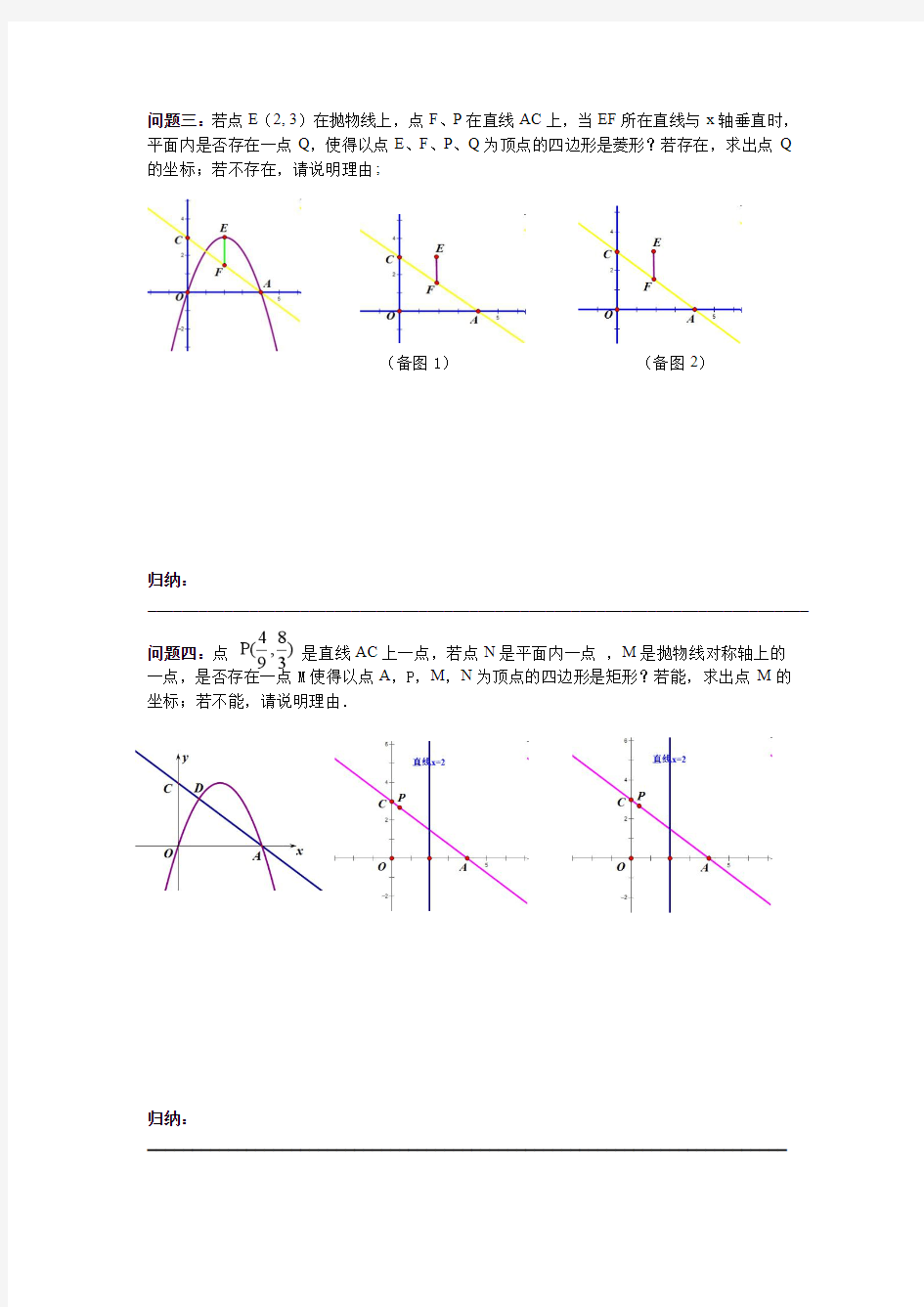
问题三:若点E(2,3)在抛物线上,点F、P在直线AC上,当EF所在直线与x轴垂直时,平面内是否存在一点Q,使得以点E、F、P、Q为顶点的四边形是菱形?若存在,求出点Q 的坐标;若不存在,请说明理由;
(备图1)(备图2)
归纳:
______________________________________________________________________________
问题四:点是直线AC上一点,若点N是平面内一点,M是抛物线对称轴上的一点,是否存在一点M使得以点A,P,M,N为顶点的四边形是矩形?若能,求出点M的坐标;若不能,请说明理由.
归纳:
_______________________________________________________________________
课后练习:
如图1,抛物线y=﹣﹣x+2与x轴交于A,B两点,与y轴交于点C,点D为线段AC的中点,直线BD与抛物线交于另一点E,与y轴交于点F.
(1)如图1,点P是直线BE上方抛物线上一动点,连接PD,PF,当△PDF的面积最大
时,在线段BE上找一点G,使得PG﹣EG的值最小,求出PG﹣EG的最小值;(2)如图2,点M为抛物线上一点,点N在抛物线的对称轴上,点K为平面内一点,当以点A、M、N、K为顶点的四边形是正方形时,直接写出点N的坐标.
平行四边形的存在性问题 【真题典藏】 1.(2008年青浦区第24题)如图1,在平面直角坐标系中,点O 是坐标原点,正比例函数kx y =(x 为自变量)的图像与双曲线x y 2 - =交于点A ,且点A 的横坐标为2-. (1)求k 的值. (2)将直线kx y =(x 为自变量)向上平移4个单位得到直线BC ,直线BC 分别交x 轴、y 轴于B 、 C ,如点 D 在直线BC 上,在平面直角坐标系中求一点P ,使以O 、B 、D 、P 为顶点的四边形是菱形. 图1 图2 2.(2009年普陀区第25题)如图2,在平面直角坐标系xOy 中,O 为原点,点A 、C 的坐标分别为(2, 0)、(1,33). 将△AOC 绕AC 的中点旋转180°,点O 落到点B 的位置,抛物线x ax y 322 -=经 过点A ,点D 是该抛物线的顶点. (1)求证:四边形ABCO 是平行四边形; (2)求a 的值并说明点B 在抛物线上; (3)若点P 是线段OA 上一点,且∠APD =∠OAB ,求点P 的坐标; (4)若点P 是x 轴上一点,以P 、A 、D 为顶点作平行四边形,该平行四边形的另一顶点在y 轴上,写出点P 的坐标. 3.(2010年上海市第24题)参见《考典40 几何计算说理与说理计算问题》第3题. 4.(2011年上海市第24题)已知平面直角坐标系xOy (如图3),一次函数3 34 y x =+的图像与y 轴交于点A ,点M 在正比例函数3 2 y x = 的图像上,且MO =MA .二次函数 y =x 2+bx +c 的图像经过点A 、M . (1)求线段AM 的长; (2)求这个二次函数的解析式;
二次函数中的平行四边形存在性问题(两定两动型) 教学设计 旬阳县城关一中黄涛 目标:1、通过典型例题及其变式训练,进一步巩固二次函数中的平行四边形及特殊平行四边形存在性问题的解题思路和方法,体会数形结合和分类讨论思想的应用过程。 2、通过本节课的学习,感受一题多解的过程及方法,提高学生分析问题和解决问题的能力。 重点:解决平行四边形存在性问题的一般方法及思路。 难点:根据条件求平行四边形的顶点中动点坐标的求解。 过程: 一、典型例题 如图,抛物线经过A(﹣1,0),B(5,0),C(0, 5 2 )三点. (1)求抛物线的解析式; (2)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由. 问题1:如何用待定系数法确定适当的解析式形式? ①抛物线上已知三点,可用一般式y=ax2+bx+c; ②因为在已知的三点中,A、B两点为抛物线与x轴交点,则可用交点式y=a(x-x 1)(x-x 2 )。 问题2:如何借助一定的方法通过画图的方式找到M、N点? 先确认已知点A、C,连接AC,根据四边形顶点的无序性利用分类讨论思想分别以AC为边和以AC为对角线两种情况进行作图讨论,作图依据平行四边形对边平行且相等的性质进 行。 问题3:通过怎样的方法和手段获取点N的坐标? 可利用以下四种方法或依据得出符合条件点N的坐标。①依据对称性求点N坐标②利用三角形全等及数形结合思想求点N坐标③依据平行四边形对边平行且相等利用平移求点N坐
标④依据抛物线解析式设点N 坐标为(m N 点与C 点纵坐标相等的原则列得绝对值方程,将所有符合条件的点N 及其坐标完全覆盖得解,注意取舍(这是本题最简方法)。 解:(1)解法1:设抛物线的解析式为y=a(x+1)(x-5) (a ≠0),将C (0,52 -)代入得: a(0+1)(0-5)=52- 解得:a=21 ∴二次函数的解析式为:y=21 (x+1)(x-5)即解法2:设抛物线的解析式为y=ax2+bx+c (a ≠0), ∴ , 解得 . ∴抛物线的解析式为: y= (2)解法1:存在,理由如下: ①以AC 为边时,当N 点位于x 轴下方时,若四边形ACNM 为平行四边形,则CN ∥AM ∴N 与C 纵坐标相等 ∴点N 与点C 关于抛物线对称轴直线x=2对称 ∴N (4,52-) 当点N 在x 轴上方时, 如图,过点N2作N2D ⊥x 轴于点D , 在△AN2D 与△M2CO 中,
备战2020年中考数学压轴题之二次函数 专题06 二次函数背景下的特殊四边形存在性判定 【方法综述】 知识准备:特殊四边形包括平行四边形、菱形、矩形和正方形。它们的判定方法如下:平行四边形的判定方法: 两组对边分别平行的四边形是平行四边形;两组对角分别相等的四边形是平行四边形 两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形 两条对角线互相平分的四边形是平行四边形; 矩形判的定方法 有一个角是直角的平行四边形是矩形;对角线相等的平行四边形是矩形 有三个角是直角的四边形是矩形 菱形判定方法 有一组邻边相等的平行四边形是菱形;对角线互相垂直的平行四边形是菱形 四条边相等的四边形是矩形 正方形的判定方法 平行四边形+矩形的特性;平行四边形+菱形的特性 解答时常用的技巧: (1).根据平行四边形的对角线互相平分这条性质,应用中点坐标公式,可以采用如下方法: 已知点A、B、C三点坐标已知,点P在某函数图像上,是否存在以点A、B、C、P为顶点的四边形为平行四边形,求点P的坐标。 如,当AP、BC为平行四边形对角线时,由中点坐标公式,可得 a+m=c+e,n+b=d+f
则m= c+e-a;n= d+f-b,点P坐标可知,将其带入到函数关系式进行验证,如果满足函数关系式,即为所求P点,同理,根据分类讨论可以得到其它情况的解答方法。 (2).菱形在折叠的情况下,可以看成是等腰三角形以底边所在直线折叠所得,因此,菱形的存在性讨论,亦可以看做等腰三角形的存在性讨论。 (3).矩形中的直角证明出来常规直角的探究外,还有主要是否由隐形圆的直径所对圆周角得到。 【典例示范】 类型一平行四边形的存在性探究 例1:如图,在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点. (1)求抛物线的解析式; (2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S,求S关于m的函数关系式,并求出S的最大值; (3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能使以点P,Q,B,O为顶点的四边形为平行四边形(要求PQ∥OB),直接写出相应的点Q的坐标. 【答案】(1)y=1 2 x2+x-4;(2)当m=-2时,S有最大值,S最大=4;(3)满足题意的Q点的坐标有三 个,分别是(-2+2-,(-2-2+,(-4,4). 【思路引导】 (1)已知抛物线与x轴的两个交点的横坐标,一般选用两点式,利用待定系数法求解即可;
中考数学解题策略专题02 平行四边形的存在性问题 专题攻略 解平行四边形的存在性问题一般分三步: 第一步寻找分类标准,第二步画图,第三步计算. 难点在于寻找分类标准,分类标准寻找的恰当,可以使解的个数不重复不遗漏,也可以使计算又好又快. 如果已知三个定点,探寻平行四边形的第四个顶点,符合条件的有3个点:以已知三个定点为三角形的顶点,过每个点画对边的平行线,三条直线两两相交,产生3个交点.如果已知两个定点,一般是把确定的一条线段按照边或对角线分为两种情况. 根据平行四边形的对边平行且相等,灵活运用坐标平移,可以使得计算过程简便.根据平行四边形的中心对称的性质,灵活运用坐标对称,可以使得解题简便. 例题解析 例?如图1-1,在平面直角坐标系中,已知抛物线 y=-x2-2x+3与x轴交于A、B两点(A在B的左侧), 与y轴交于点C,顶点为P,如果以点P、A、C、D为 顶点的四边形是平行四边形,求点D的坐标. 图1-1 例?如图2-1,在平面直角坐标系中,已知抛物线y=-x2+2x+3与x轴交于A、B两点,点M在这条抛物线上,点P在y轴上,如果以点P、M、A、B为顶点的四边形是平行四边形,求点M的坐标. 图2-1
例? 如图3-1,在平面直角坐标系中,直线y =-x +4与x 轴交于点A ,与y 轴交于点B ,点C 在直线AB 上,在平面直角坐标系中求一点D ,使得以O 、A 、C 、D 为顶点的四边形是菱形. 图 3-1 例? 如图4-1,已知抛物线241633 y x x =+与x 轴的负半轴交于点C ,点E 的坐标为(0,-3),点N 在抛物线的对称轴上,点 M 在抛物线上,是否存在这样的点M 、N ,使得以M 、N 、C 、E 为顶点的四边形是平行四边形?若存在,请求出点M 的坐标;若 不存在,请说明理由. 图4-1 例?如图1,在平面直角坐标系中,抛物线y =ax 2-2ax -3a (a <0)与x 轴交于A 、B
专题:二次函数中的平行四边形存在性问题 类型一:已知三个定点,再找一个定点构成平行四边形(平面内有三个点满足) 1.已知抛物线b ax ax y ++-=22与x 轴的一个交点为A (-1,0),与y 轴的正半轴交于点C. ⑴直接写出抛物线的对称轴,及抛物线与x 轴的另一个交点B 的坐标; ⑵当点C 在以AB 为直径的⊙P 上时,求抛物线的解析式; ⑶坐标平面内是否存在点M ,使得以点M 和⑵中抛物线上的三点A、B、C 为顶点的四边形是平行四边形?若存在,请求出点M 的坐标;若不存在,请说明理由. 类型:已知两个定点,再找两个点构成平行四边形 1.已知,如图抛物线2 3(0)y ax ax c a =++>与y 轴交于C 点,与x 轴交于A、B 两点,A 点在B 点左侧。点B 的坐标为(1,0),OC=30B. (1)求抛物线的解析式; (2)若点D 是线段AC 下方抛物线上的动点,求四边形ABCD 面积的最大值: (3)若点E 在x 轴上,点P 在抛物线上。是否存在以A、C、E、P 为顶点且以AC 为一边的平行四边形?若存在,求点P 的坐标;若不存在,请说明理由.
2、练习如图,抛物线:c bx x y ++=22 1与x 轴交于A、B(A 在B 左侧),顶点为C(1,﹣2)。(1)求此抛物线的关系式;并直接写出点A、B 的坐标; (2)求过A、B、C 三点的圆的半径; (3)在抛物线上找点P,在y 轴上找点E,使以A、B、P、E 为顶点的四边形是平行四边形,求点P、E 的坐标。 1.如图,抛物线2 23y x x =--与x 轴交A、B 两点(A 点在B 点左侧),直线l 与抛物线交于A、C 两点,其中C 点的横坐标为2. (1)求A、B 两点的坐标及直线AC 的函数表达式; (2)P 是线段AC 上的一个动点,过P 点作y 轴的平行线交抛物线于E 点,求线段PE 长度的最大值; (3)点G 抛物线上的动点,在x 轴上是否存在点F,使A、C、F、G 这样的四个点为顶点的四边形是平行 四边形?如果存在,求出所有满足条件的F 点坐标;如果不存在,请说明理由.
二次函数中动点与特殊四边形综合问题解析与训练 一、知识准备: 抛物线与直线形的结合表形式之一是,以抛物线为载体,探讨是否存在一些点,使其能构成某些特殊四边形,有以下常风的基本形式 (1)抛物线上的点能否构成平行四边形 (2)抛物线上的点能否构成矩形,菱形,正方形 特殊四边形的性质与是解决这类问题的基础,而待定系数法,数形结合,分类讨论是解决这类问题的关键。 二、例题精析 ㈠【抛物线上的点能否构成平行四边形】 例一、(2013河南)如图,抛物线2 y x bx c =-++与直线 1 2 2 y x =+交于,C D两点,其 中点C在y轴上,点D的坐标为 7 (3,) 2 。点P是y轴右侧的抛物线上一动点,过点P作 PE x ⊥轴于点E,交CD于点F. (1)求抛物线的解析式; (2)若点P的横坐标为m,当m为何值时,以,,, O C P F为顶点的四边形是平行四边形?请说明理由。 【解答】(1)∵直线 1 2 2 y x =+经过点C,∴(0,2) C ∵抛物线2 y x bx c =-++经过点(0,2) C,D 7 (3,) 2
∴22727 332 2c b b c c =?? =? ?∴??=-++??=?? ∴抛物线的解析式为2 7 22 y x x =-++ (2)∵点P 的横坐标为m 且在抛物线上 ∴2 71 (,2),(,2)22 P m m m F m m -+ ++ ∵PF ∥CO ,∴当PF CO =时,以,,,O C P F 为顶点的四边形是平行四边形 ① 当03m <<时,2 271 2(2)322 PF m m m m m =-+ +-+=-+ ∴2 32m m -+=,解得:121,2m m == 即当1m =或2时,四边形OCPF 是平行四边形 ② 当3m ≥时,2 217 (2)(2)32 2 PF m m m m m =+--+ +=- 232m m -= ,解得:123322 m m += =(舍去) 即当132 m += 时,四边形OCFP 是平行四边形 练习1:(2013?盘锦)如图,抛物线y=ax 2+bx+3与x 轴相交于点A (﹣1,0)、B (3,0), 与y 轴相交于点C ,点P 为线段OB 上的动点(不与O 、B 重合),过点P 垂直于x 轴的直线与抛物线及线段BC 分别交于点E 、F ,点D 在y 轴正半轴上,OD=2,连接DE 、OF . (1)求抛物线的解析式; (2)当四边形ODEF 是平行四边形时,求点P 的坐标;
一次函数与特殊四边形的存在性问题 (培优专题) 1.(2015春?通州区校级期中)如图,在直角坐标系中,A(0,1),B(0,3),P是x轴上一动点,在直线y=x上是否存在点Q,使以A、B、P、Q为顶点的四边形为平行四边形?若存在,画出所有满足情况的平行四边形,并求出对应的P、Q的坐标;若不存在,请说明理由. 2.(2015春?北京校级期中)已知直线y=x+3分别交x轴、y轴于点A、B. (1)求∠BAO的平分线的函数关系式;(写出自变量x的取值范围) (2)点M在已知直线上,点N在坐标平面内,是否存在以点M、N、A、O 为顶点的四边形为菱形?若存在,请直接写出点N的坐标;若不存在,说明理由.
3.(2010秋?吴江市校级期中)已知:如图,在矩形ABCD中,点E在AD 边上,AE>DE,BE=BC,点O是线段CE的中点. (1)试说明CE平分∠BED; (2)在直线AD上是否存在点F,使得以B、C、F、E为顶点的四边形是菱形?如果存在,试画出点F的位置,并作适当说明;如果不存在,请说明理由. 4.如图,在平面直角坐标系xOy,直线y=x+1与y=﹣2x+4交于点A,两直线与x轴分别交于点B和点C,D是直线AC上的一个动点,直线AB上是否存在点E,使得以E,D,O,A为顶点的四边形是平行四边形?若存在,求出点E的坐标;若不存在,请说明理由.
5.如图,点A的坐标是(2,1),点B的坐标是(5,1),过点A的直线l 的表达式为y=2x+b,点C在直线l上运动,在直线OA上是否存在一点D,使得以A,B,C,D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由. 6.(2012春?雨花区校级期末)如图,已知等边△ABC的边长为2,顶点A、B分别在x轴、y轴的正半轴上移动. (1)当OA=时,求点C的坐标. (2)在(1)的条件下,求四边形AOBC的面积. (3)是否存在一点C,使线段OC的长有最大值?若存在,请求出此时点C 的坐标;若不存在,请说明理由.
A B M 1 M 3 在几何中,平行四边形的判定方法有如下几条:①两组对边互相平行;②两 组对边分别相等;③一组对边平行且相等;④对角线互相平分;⑤两组对角相等。在压轴题中,往往与函数(坐标轴)结合在一起,运用到④⑤的情况较少,更多的是从边的平行、相等角度来得到平行四边形。 1、知识容: 已知三点后,其实已经固定了一个三角形(平行四边形的一半),如图△ABC .第四个点M 则有3种取法,过3个顶点作对 平行四边形的存在性问题 知识结构 知识精讲 模块一:已知三点的平行四边形问题 知识概述 平行四边形的存在性问题 已知三点的平行四边形问题 存在动边的平行四边形问题
边的平行线且取相等长度即可(如图中3个M点). 2、解题思路: (1)根据题目条件,求出已知3个点的坐标; (2)用一点及其对边两点的关系,求出一个可能点; (3)更换顶点,求出所有可能的点; (4)根据题目实际情况,验证所有可能点是否满足要求并作答.例题解析 【例1】如图,抛物线y=x2+bx-c经过直线y=x-3与坐标轴的两个交点A、B,此抛物线与x轴的另一个交点为C,抛物线的顶点为D. (1)求此抛物线的解析式; (2)点P为抛物线上的一个动点,求使S△APC︰S△ACD=5 ︰4的点P的坐标; (3)点M为平面直角坐标系上一点,写出使点M、A、B、 D为平行四边形的点M的坐标.
【例2】如图,已知抛物线y=ax2+3ax+c与y轴交于点C,与x轴交于A、B两点(点A 在点B的左侧),点B的坐标为(1, 0),tan∠OBC=3. (1)求抛物线的解析式; (2)点E在x轴上,点P在抛物线上,是否存在以 A、C、E、P为顶点且以AC为一边的平行四边形,若存 在,写出点P的坐标; (3)抛物线的对称轴与AC交于点Q,说明以Q为 圆心,以OQ为半径的圆与直线BC的关系.
学习必备欢迎下载 问题 1:存在性问题的处理框架是什么? 问题 2:两定两动的平行四边形存在性问题的分类标准是什么? 1. 如图,将矩形OABC 放置在平面直角坐标系中,OA=8, OC=12,直线与x 轴交于点D,与 y 轴交于点E,把矩形沿直线DE翻折,点 O 恰好落在AB 边上的点 F 处,M 是直线 DE 上的一个动点,直线DF 上是否存在点N,使以点 C,D,M ,N 为顶点的四边形是平行四边形?则符合题意的点N 的坐标是? 2.如图,在平面直角坐标系中,直线与交于点A,与x 轴分别交于 点 B 和点 C, D 是直线 AC上一动点, E 是直线AB 上一动点.若以O, D, A,E 为顶点的四边形是平行四边形,则点 E 的坐标为? 反思与总结: 问题 1:平行四边形存在性问题的处理框架中第一步:研究背景图形,需要研究哪些内容? 问题 2:画出对应图形后求解点坐标的套路是什么?
练习 1.如图,直线与 x 轴、 y 轴分别交于A, B 两点,直线BC x 轴交于点C,且 与 ∠ABC=60°,若点 D 在直线AB 上运动,点E在直线 BC 上运动,且以O, B, D,E 为顶点的 四边形是平行四边形,则点 D 的坐标为 ( ) 2..如图,在平面直角坐标系中,矩形OABC的对角线AC=12,∠ ACO=30°,把矩形沿直线 DE 翻折,使点 C 落在点 A 处, DE 与 AC 相交于点 F,若点 M 是直线 DE上一动点,点N 是直线 AC 上一动点,且以O,F,M , N 为顶点的四边形是平行四边形,则点N 的坐标为 () 3.如图,直线分别交x轴、y轴于A,B两点,线段AB 的垂直平分线交x 轴于 点 C,交 AB 于点 D.若在平面内存在点 E,使得以点 A,C,D,E 为顶点的四边形是平行四边 形,则点 E 的坐标为
?? ?? 探究特殊四边形存在性问题 1.如图,抛物线y=x2-2x-3经过点A(2,-3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB. (1)求点B,C的坐标; (2)若点D在y轴上,且∠BDO=∠BAC,求点D的坐标; (3)若点M为抛物线上一点,点N在抛物线的对称轴上,是否存在以点A、B、M、N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标,若不存在,请说明理由. 第1题图 解:(1)令x=0得y=-3, ∴C(0,-3), ∴OC=3, ∵OC=3OB, ∴OB=1, ∴B(-1,0), 把A(2,-3),B(-1,0)分别代入y=ax2+bx-3得: ?a-b-3=0?a=1 ?,解得?, ?4a+2b-3=-3?b=-2 ∴抛物线的解析式为y=x2-2x-3; (2)如解图①,过点B作BE⊥AC,交AC延长线于点E. 第1题解图① ∵C(0,-3),A(2,-3), ∴AC∥x轴, ∴BE=3, 又∵OB=1, ∴AE=3,∴AE=BE,
∴∠BAE=45°, ∵∠BDO=∠BAC=45°, ∴OB=OD, ∴D点的坐标为(0,1)或(0,-1), (3)存在.如解图②. 第2题解图② 当AB∥MN时,由AB=MN=32,可知点M与对称轴的距离为3,由y=x2-2x-3可得对称轴为直线x=1, ∴点M的横坐标为4或-2,把x=4和-2分别代入y=x2-2x-3可得点M坐标, 把x=-2代入y=x2-2x-3得y=4+4-3=5, (-2,5). ∴M 1 把x=4代入y=x2-2x-3得y=16-8-3=5, (4,5), ∴M 2 当MN与AB互相平分时,四边形AMBN是平行四边形,由AC=BN=2,可知点M与点C重合,∴点M3坐标为(0,-3), ∴M的坐标为(-2,5)或(0,-3)或(4,5). 2.如图,抛物线顶点P(1,4),与y轴交于点C(0,3),与x轴交于点A,B. (1)求抛物线的解析式; (2)Q是抛物线上除点P外一点,△BCQ与△BCP的面积相等,求点Q的坐标; (3)若M,N为抛物线上两个动点,分别过点M,N作直线BC的垂线段,垂足分别为D,E,是否存在点M,N使四边形MNED为正方形?如果存在,求正方形MNED的边长;如果不存在,请说明理由. 第2题图 解:(1)设抛物线解析式为:y=a(x-1)2+4(a≠0). ∵抛物线过点C(0,3), ∴a+4=3,∴a=-1. ∴y=-(x-1)2+4=-x2+2x+3; (2)由(1)得,抛物线的解析式为y=-x2+2x+3,
二次函数中的平行四边形存在性问题 目标:1、通过本节课的学习,提高学生分析问题,解决问题的能力。 2、能总结出解决平行四边形存在性问题的一般方法和思路。重点:解决平行四边形存在性问题的一般方法及思路。 难点:根据条件求平行四边形的顶点坐标。 过程: 一、复习 1、平行四边形的性质 角: 边; 对角线: 2、二次函数的相关知识点 表达式、顶点坐标、对称轴、增减性 二、探索新知 1、単动点(知3点求1点) (1)已知平面上有不在同一条直线上的三点A、B、C,点D是平面上任一点,若此四点能构成平行四边形则符合条件的D点有几个? ()
学生画图说明 思考:如何找第四点?找第四点的方法? (2)类题 (1)已知抛物线与坐标轴分别交于A(-1、0)、B (3、0)、C (0、3)三点,能否在平面内在找一点D使得它们四点围成的四边形为平行四边形? 学生分析总结规律、思路。 ①、根据平行四边形的边、对角线的性质(对边平行且相等, 对角线互相平分)我们可以选择一种情况作为画图的依据。 ②、在求点的坐标时(以边为例)我们先满足对边平行再用对 边相等求出要求的点的坐标。
2、 双动点(知2点求2点) (1) 学生再次画图说明(给出两点画出另外两点) (2)类题 如图,抛物线y= 13 x 2-mx+n 与x 轴交于A 、B 两点,与y 轴交于点C (0.-1).且对称轴x=l . ① 求出抛物线的解析式及A 、B 两点的坐标; ② 点Q 在y 轴上,点P 在抛物线上,要使Q 、P 、A 、B 为顶点的四边形是平行四边形,请求出所有满足条件的点P 的坐标。
点A,点B是定点 点P,点Q是动点 分两种情况:AB为边,AB为对角线 3、小结 4、布置作业 5、
《二次函数专题提优》:特殊四边形存在性问题 (一)、平行四边形存在性原理: 1、实验与探究: (1)、在图1,2,3中,给出平行四边形ABCD的顶点A B D ,,的坐标(如图所示),写出图1,2,3中的顶点C的坐标,它们分别是(52) , ,,; ( 2)、在图4 中,给出平行四边形ABCD 的顶点A B D ,,的坐标(如图所示),求出顶点C的坐标(C点坐标用含 a b c d e f ,,,,,的代数式表示); 归纳与发现: (3)、通过对图1,2,3,4的观察和顶点C的坐标的探究,你会发现:无论平行四边形ABCD处于直角坐标系中哪个位置,当其顶点坐标为 ()()()() A a b B c d C m n D e f ,,,,,,,(如图4)时,则四个顶点的横坐标a c m e ,,,之间的等量关系为;纵坐标b d n f ,,,之间的等量关系为(不必证明); 运用与推广: (4)、在同一直角坐标系中有抛物线 2(53) y x c x c =---和三个点 1519 2222 G c c S c c ???? - ? ? ???? ,,, , (20) H c,(其 中0 c>).问当c为何值时,该抛物线上存在点P,使得以G S H P ,,,为顶点的四边形是平行四边形? 并求出所有符合条件的P点坐标. 图1图2图3 图4
(二)、平行四边形的存在性问题: 2、在平面直角坐标系xOy 中,已知抛物线 c bx ax y + + =2的对称轴是x=1,并且经过(?2,?5)和(5,?12)两点。 (1)、求此抛物线的解析式; (2)、设此抛物线与x轴交于A. B 两点(点A 在点B的左侧),与y轴交于C 点,D是线段BC上一点(不与点B. C 重合),若以B. O、D为顶点的三角形与△BAC相似,求点D的坐标; (3)、点P在y轴上,点M在此抛物线上,若要使以点P、M、A. B为顶点的四边形是平行四边形, 请你直接写出点M的坐标 3、如图,抛物线y=ax2+bx+c交x轴于点A(-3,0),点B(1,0),交y轴于点E(0,-3),点C是点A关于点B 的对称点,点F是线段BC的中点,直线l过点F且与y轴平行,直线y=-x+m过点C,交y轴于点D. (1)、求抛物线的函数表达式; (2)、点K为线段AB上一动点,过点K作x轴的垂线与直线CD交于点H,与抛物线交于点G,求线段HG长度的最大值; (3)、在直线l上取点M,在抛物线上取点N,使以点A,C,M,N为顶点的四边形是平行四边形,求点N的坐标. A x B C D H E F G K O x y l A B C D H E F G K O y l 备用图 图①
常见四边形的存在性 专题一、平行四边形的存在性问题 一、技巧提炼 模型:平行四边形模型探究 如图1,点A ()11,x y 、B ()22,x y 、C ()33,x y 是坐标平面内不在同一直线上的三点。平面直角坐标系中是否存在点D ,使得以A 、B 、C 、D 四点为顶点的四边形为平行四边形,如果存在,请求出点D 的坐标。 A B C x y 图1 图2 如图2,过A 、B 、C 分别作BC 、AC 、AB 的平行线,则以不在同一直线上的三点为顶点的平行四边形有三个。由已知的三点坐标可根据图形平移的坐标性质,直接写出第四个顶点的坐标。 解题思路:(1)先分类(2)再画图(3)后计算 例1.(2015?贵阳)如图,经过点C (0,﹣4)的抛物线y=ax 2 +bx+c (a≠0)与x 轴相交于A (﹣2,0),B 两点. (1)a > 0,b 2 ﹣4ac > 0(填“>”或“<”); (2)若该抛物线关于直线x=2对称,求抛物线的函数表达式; (3)在(2)的条件下,连接AC ,E 是抛物线上一动点,过点E 作AC 的平行线交x 轴于点F .是否存在这样的点E ,使得以A ,C ,E ,F 为顶点所组成的四边形是平行四边形若存在,求出满足条件的点E 的坐标;若不存在,请说明理由.
【考点】二次函数综合题. 【专题】综合题;压轴题. 【分析】(1)根据抛物线开口向上,且与x轴有两个交点,即可做出判断; (2)由抛物线的对称轴及A的坐标,确定出B的坐标,将A,B,C三点坐标代入求出a,b,c的值,即可确定出抛物线解析式; (3)存在,理由为:假设存在点E使得以A,C,E,F为顶点所组成的四边形是平行四边形,过点C作CE∥x轴,交抛物线于点E,过点E作EF∥AC,交x轴于点F,如图1所示;假设在抛物线上还存在点E′,使得以A,C,F′,E′为顶点所组成的四边形是平行四边形,过点E′作E′F′∥AC交x轴于点F′,则四边形ACF′E′即为满足条件的平行四边形,可得AC=E′F′,AC∥E′F′,如图2,过点E′作E′G⊥x轴于点G,分别求出E坐标即可.【解答】解:(1)a>0,b2﹣4ac>0; (2)∵直线x=2是对称轴,A(﹣2,0), ∴B(6,0), ∵点C(0,﹣4),将A,B,C的坐标分别代入y=ax2+bx+c,
网课:二次函数中特殊四边形的存在性问题 学习目标: 1、通过二次函数中的特殊四边形存在性问题的探究、学习,获取解决这类问题的基本方法;经历解决二次函数中的特殊四边形存在性问题的探索过程,培养学生的理解能力,抽象能力,能正确认识问题的本质,提高知识迁移能力,积累解决问题的经验,感受数学知识对解决问题的价值; 2、通过函数中的特殊四边形存在性问题的解决,渗透“转化”、“分类”、“方程”、“数形结合”等数学思想,并在问题解决中体验成功的快乐,感受数学的魅力. 学习重点:利用“特殊四边形的性质”,或者“点在函数上”来建立等量关系,解决“点是否存在的问题”. 学习难点:从复杂的函数背景中提炼问题的本质,利用“特殊四边形的性质”,或者“点在函数上”来建立等量关系,解决“点是否存在的问题”. 背景问题: 如图,抛物线中,点A在x轴的正半轴上,点C在y轴的正半轴上, OC=3,点D是直线AC与抛物线的交点。 问题一:在平面内是否存在一点B,使得以A、B、O、D为顶点的 四边形是平行四边形? 若存在,请直接写出B点的坐标;若不存在,请说明理由。 归纳:_________________________________________________ 问题二:若点M在抛物线上,点N在x轴上,是否存在以A、D、M、N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由; (备图1)(备图2) 归纳: _____________________________________________________________________________
问题三:若点E(2,3)在抛物线上,点F、P在直线AC上,当EF所在直线与x轴垂直时,平面内是否存在一点Q,使得以点E、F、P、Q为顶点的四边形是菱形?若存在,求出点Q 的坐标;若不存在,请说明理由; (备图1)(备图2) 归纳: ______________________________________________________________________________ 问题四:点是直线AC上一点,若点N是平面内一点,M是抛物线对称轴上的一点,是否存在一点M使得以点A,P,M,N为顶点的四边形是矩形?若能,求出点M的坐标;若不能,请说明理由. 归纳: _______________________________________________________________________
一次函数与平行四边形 1.线段中点公式 平面直角坐标系中,点A 坐标为(x 1,y 1),点B 坐标为(x 2,y 2), 则线段AB 的中点P 的坐标为 (2,22121y y x x ++) 例:如图,已知点A (-2,1),B (4,3),则线段AB 的中点P 的坐标是________. 2.线段的平移 平面内,线段AB 平移得到线段A'B' ,则①AB ∥A'B' ,AB =A'B' ;②AA'∥BB',AA'= BB'. 如图,线段AB 平移得到线段A'B' ,已知点A (-2,2),B (-3,-1), B' (3,1),则点A'的坐标是________. 例:如图,在平面直角坐标系中,□ABCD 的顶点坐标分别为A (x 1,y 1)、B (x 2,y 2)、C (x 3,y 3)、D (x 4,y 4),已知其中3个顶点的坐标,如何确定第4个顶点的坐标? 例:如图,已知□ABCD 中A (-2,2),B (-3,-1), C (3,1),则点D 的坐标是________. 方法一:利用线段平移 总结:x 1-x 2= x 4-x 3,y 1-y 2= y 4-y 3 或者 x 4-x 1= x 3-x 2,y 4-y 1= y 3-y 2 等 方法二:利用中点公式 总结:x 1+x 3= x 2+x 4,y 1+y 3= y 2+y 4
类型一:三定一动 例1 、如图,平面直角坐标中,已知中A (-1,0),B (1,-2),C (3,1),点D是平面内一动点,若以点A、B、C、D为顶点的四边形是平行四边形,则点D的坐标是_________________________________. 总结:三定一动问题,可以通过构造中点三角形得以解决. 说明:若题中四边形ABCD是平行四边形,则点D的坐标只有一个结果________
四边形之存在性问题(讲义) 课前预习 一般悄况下我们如何处理存在性问题? (1) 研究背景图形 坐标系背景下研究 ____________ 、 ______ 究 ___________ 、 ____________ 、 ______ (2) 根据不变特征,确定分类标准 研究定点,动点,定线段,确定分类标准 不变特征举例: ① 等腰三角形(两定一动) 以定线段作为 ________ 或者— _______________ 确定点的位 ② 置.等腰直角三角形(两定 一动) 以 知识点睛 存在性问题处理框架: ① 研究背景图形. ② 根据不变特征,确定分类标准. ③ 分析特殊状态的形成因素,画出符合题意的图形并求解. ④ 结果验证. 平行四边形存在性问题特征举例: 分析定点、动点. ① 三定一动,连接定点出现三条定线段.定线段分别作 为平行四边形的 _________ ,利用 _____________ 确定 点坐标. ② 两定两动,连接定线段,若定线段作为平行四边形的 ________ ,则通过 ___________ 确定点的坐标;若定线 段作为平行四边形的 ___________ ,则定线段绕 __________ 旋转,利用 _______________ 确定点的坐标. 结合图形进行验证. ;儿何图形研 或者 来分类,利用 来分类,然后借助 确定点的位置. (3) 分析特殊状态的形成因素,画出符合题意的图形并求解 (4) 结果验证 2. (1) (2)
3.特殊平行四边形存在性问题不变特征举例: ①菱形存在性问题(两定两动) 转化为等腰三角形存在性问题; 以定线段作为底边或者腰确定分类标准,利用两圆一线确定一动点的位置,然后通过平移确定另一动点坐标. ②正方形存在性问题(两定两动) 转化为等腰直角三角形存在性问题; 根据直角顶点确定分类标准,利用两腰相等或者45。角确定一动点的位置,然后通过平移确定另一动点坐标. 2如图,在平面直角坐标系中,直线y = -?x + 3与X轴、>' 4 轴分别交于点A, 点C的坐标为(0, -2 ).若点D在直线 AB上运动,点E在直线AC±运动,当以0, 4, D, E为顶点的四边形是平行四边形时,求点D的坐标.
二次函数平行四边形存在性问题例题 一.解答题(共9小题) 1.如图,抛物线经过A(﹣1,0),B(5,0),C(0,)三点. (1)求抛物线的解析式; (2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由. 2.如图,在平面直角坐标系中,直线y=﹣3x﹣3与x轴交于点A,与y轴交于点C.抛物线y=x2+bx+c经过A,C两点,且与x轴交于另一点B(点B在点A右侧).(1)求抛物线的解析式及点B坐标; (2)若点M是线段BC上一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值; (3)试探究当ME取最大值时,在x轴下方抛物线上是否存在点P,使以M,F,B,P 为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由. 3.已知:如图,在平面直角坐标系xOy中,直线与x轴、y轴的交点分别为A、B两点,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x
轴于点C. (1)直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式; (2)若(1)中抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP 为平行四边形?若存在,求出点P的坐标;若不存在,说明理由; (3)若把(1)中的抛物线向左平移3.5个单位,则图象与x轴交于F、N(点F 在点N的左侧)两点,交y轴于E点,则在此抛物线的对称轴上是否存在一点Q,使点Q到E、N两点的距离之差最大?若存在,请求出点Q的坐标;若不存在,请说明理由. 4.已知:如图,在平面直角坐标系xOy中,直线与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C. (1)直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式; (2)若抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP为平行四边形?若存在,求出点P的坐标;若不存在,说明理由; (3)设抛物线的对称轴与直线BC的交点为T,Q为线段BT上一点,直接写出|QA﹣QO|的取值范围. 5.如图,Rt△OAB如图所示放置在平面直角坐标系中,直角边OA与x轴重合,∠
四边形之存在性问题(二)(讲义) 课前预习 1.一般情况下我们如何处理存在性问题? (1)研究背景图形 坐标系背景下研究、;几何图形研究、、. (2)根据不变特征,确定分类标准 研究定点,动点,定线段,确定分类标准 不变特征举例: ①等腰三角形(两定一动) 以定线段作为或者来分类,利用 确定点的位置. ②等腰直角三角形(两定一动) 以来分类,然后借助或者 确定点的位置. (3)分析特殊状态的形成因素,画出符合题意的图形并求解(4)结果验证 2.用铅笔做讲义第1,2 题,并将计算、演草保留在讲义上,先 看知识点睛,再做题,思路受阻时(某个点做了2~3 分钟)重复上述动作,若仍无法解决,课堂重点听. 知识点睛 1.存在性问题处理框架: ①研究背景图形. ②根据不变特征,确定分类标准. ③分析特殊状态的形成因素,画出符合题意的图形并求解. ④结果验证. 2.特殊平行四边形存在性问题不变特征举例: ①菱形存在性问题(两定两动) 转化为等腰三角形存在性问题; 以定线段作为底边或者腰确定分类标准,利用两圆一线确定一动点的位置,然后通过平移确定另一动点坐标. ②正方形存在性问题(两定两动)转 化为等腰直角三角形存在性问题; 根据直角顶点确定分类标准,利用两腰相等或者45°角确定一动点的位置,然后通过平移确定另一动点坐标.
精讲精练 1.如图,在平面直角坐标系xOy 中,直线l:y = 2x - 4 与x 轴交 于点A,与y 轴交于点B. (1)求点A,B 的坐标. (2)若P 是直线x =-2 上的一动点,则在坐标平面内是否存在点Q,使得以A,B,P,Q 为顶点的四边形是菱形?若存在,求出点Q 的坐标;若不存在,请说明理由.
●探究 (1)在图1中,已知线段AB,CD,其中点分别为E,F。 ①若A(-1,0),B(3,0),则E点坐标为__________; ②若C(-2,2),D(-2,-1),则F点坐标为__________; (2)在图2中,已知线段AB的端点坐标为A(a,b),B(c,d),求出图中AB中点D的坐标(用含a,b,c,d的代数式表示),并给出求解过程; ●归纳 无论线段AB处于直角坐标系中的哪个位置, 当其端点坐标为A(a,b),B(c,d),AB中点为D(x,y)时,x=_________,y=___________;(不必证明) ●运用 在图2中,一次函数y=x-2与反比例函数的图象交点为A,B。 ①求出交点A,B的坐标; ②若以A,O,B,P为顶点的四边形是平行四边形,请利用上面的结论求出顶点P的坐标。
图 2 图 3 图1 以二次函数为载体的平行四边形存在性问题是近年来中考的热点,其图形复杂,知识覆盖面广,综合性较强,对学生分析问题和解决问题的能力要求高.对这类题,常规解法是先画出平行四边形,再依据“平行四边形的一组对边平行且相等”或“平行四边形的对角线互相平分”来解决.由于先要画出草图,若考虑不周,很容易漏解.为此,笔者另辟蹊径,借助探究平行四边形顶点坐标公式来解决这一类题. 1 两个结论,解题的切入点 数学课标,现行初中数学教材中没有线段的中点坐标公式,也没有平行四边形的顶点坐标公式,我们可帮助学生来探究,这可作为解题的切入点。 1.1 线段中点坐标公式 平面直角坐标系中,点A 坐标为(x 1,y 1),点B 坐标为(x 2,y 2),则线段AB 的中点坐标为(221x x +,2 21y y +). 证明 : 如图1,设AB 中点P 的坐标为(x P ,y P ).由x P -x 1=x 2-x P ,得x P = 2 21x x +,同理y P =221y y +,所以线段AB 的中点坐标为(221x x +,221y y +). 1.2 平行四边形顶点坐标公式 □ABCD 的顶点坐标分别为A (x A ,y A )、B (x B ,y B )、C (x C ,y C )、D (x D ,y D ),则:x A +x C =x B +x D ;y A +y C =y B +y D . 证明: 如图2,连接AC 、BD ,相交于点E . ∵点E 为AC 的中点, ∴E 点坐标为(2C A x x +,2 C A y y +). 又∵点E 为B D 的中点, ∴ E 点坐标为( 2D B x x +,2D B y y +). ∴x A +x C =x B +x D ;y A +y C =y B +y D . 即平行四边形对角线两端点的横坐标、纵坐标之和分别相等. 2 一个基本事实,解题的预备知识 如图3,已知不在同一直线上的三点A 、B 、C ,在平面内另找一个点D ,使以A 、B 、C 、D 为顶点的四边形是平行四边形.答案有三种:以AB 为对角线的□ACBD 1,以AC 为对角线的□ABCD 2,以BC 为对角线的□ABD 3C .