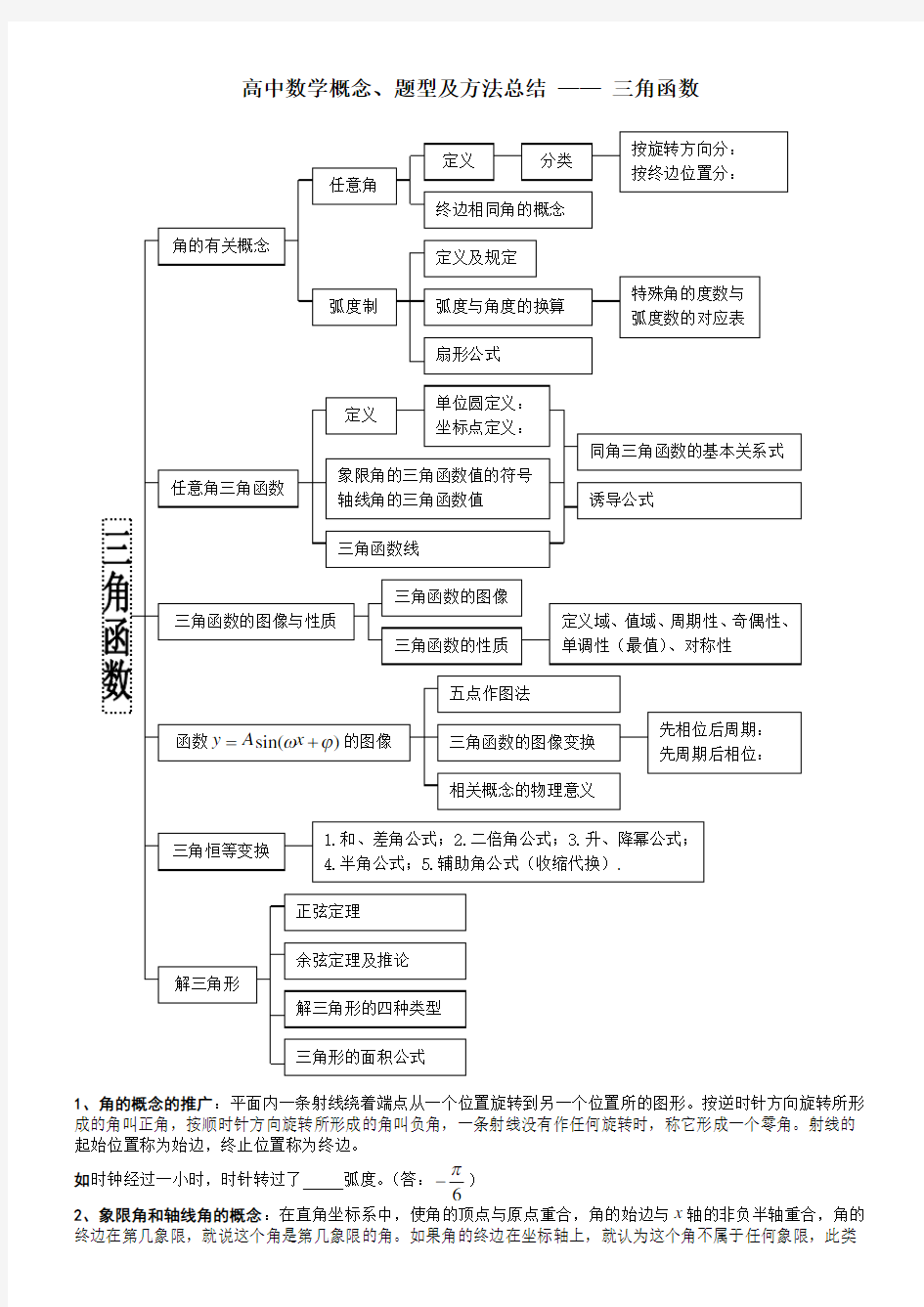
高中数学概念题型及方法总结三角函数

高中数学概念、题型及方法总结 —— 三角函数

1、角的概念的推广：平面内一条射线绕着端点从一个位置旋转到另一个位置所的图形。按逆时针方向旋转所形成的角叫正角，按顺时针方向旋转所形成的角叫负角，一条射线没有作任何旋转时，称它形成一个零角。射线的起始位置称为始边，终止位置称为终边。

如时钟经过一小时，时针转过了 弧度。（答：6

π

-

） 2、象限角和轴线角的概念：在直角坐标系中，使角的顶点与原点重合，角的始边与x 轴的非负半轴重合，角的终边在第几象限，就说这个角是第几象限的角。如果角的终边在坐标轴上，就认为这个角不属于任何象限，此类

角称为轴线角。

如若3-=α，则角α的终边在第 象限。（答：三） 3、终边相同的角的表示：

（1）α终边与θ终边相同?2()k k αθπ=+∈Z ，注：相等的角的终边一定相同，终边相同的角不一定相等. 如与角ο

1825-终边相同，且绝对值最小的角度数是＿＿，合＿＿弧度。 （答：25-o

；5

36

π-） （2）α终边与θ终边共线(α的终边在θ终边所在直线上) ?()k k αθπ=+∈Z . （3）α终边与θ终边关于x 轴对称?2()k k αθπ=-+∈Z . （4）α终边与θ终边关于y 轴对称?2()k k απθπ=-+∈Z . （5）α终边与θ终边关于原点对称?2()k k απθπ=++∈Z .

（6）α终边在x 轴上的角可表示为：,k k Z απ=∈；α终边在y 轴上的角可表示为：,2

k k Z π

απ=+∈；α

终边在坐标轴上的角可表示为：,2

k k Z π

α=∈. 如1）α的终边与

6π的终边关于直线x y =对称，则α＝____________。 （答：Z k k ∈+,3

2π

π） 2）若α是第四象限角，则απ-是第 象限角。 （答：三） 4、α与2

α的终边关系：由“两等分各象限、一二三四”确定.

如若α是第二象限角，则

2

α

是第_____象限角 （答：一、三） 5、与角有关的集合问题：关键是弄清集合中含有哪些元素。方法有：一是将集合中表示角的式子化为同一结构形式；二是用列举法把集合具体化；三是数形结合，即在坐标系中作这些角。 如已知集合{}Z k k M ∈?±==

,90)14(0

αα，{}Z k k N ∈?+==,90)12(0

ββ，则M 与N 的关系如何？

（答：相等）

6、弧长公式：||l R α=，扇形面积公式：2

11||2

2

S lR R α==

角度与弧度的转换：1

=rad rad 01745.0180≈π

，'185730.571801ο

οο

=≈??

? ??=πrad 如已知扇形的周长是40cm ，当它的半径和圆心角分别取何值时，才能使扇形的面积最大？最大面积是多少？ （答：当半径为10cm ，圆心角为2rad 时，扇形的面积最大，为1002

cm ）

7、任意角的三角函数的定义：

单位圆定义：设α是一个任意角,它的终边与单位圆交于点(,)P x y ,

那么sin y α=，cos x α=， tan (0)y

x x

α=

≠. 坐标点定义：设α是任意一个角，P (,)x y 是α的终边上的任意一点（异于原点），

它与原点的距离是220r x y =

+>，那么sin ,cos y x r r αα=

=，()tan ,0y

x x

α=≠。 如（1）已知角α的终边经过点P(5，－12)，则ααcos sin +的值为＿＿。（答：7

13

-）；

（2）设α是第三、四象限角，m m --=432sin α，则m 的取值范围是_______（答：（－1，)2

3

）；

8、三角函数线的特征是：正弦线MP “站在x 轴上(起点在x 轴上)”、余弦线OM “躺在x 轴上(起点是原点)”、正切线AT “站在点(1,0)A 处(起点是A )”.

（2

9

10、同角三角函数的基本关系式：

（1）平方关系：22

sin cos 1,1tan sec ,1cot csc αααααα+=+=+= （2）商数关系：sin cos tan ,cot

cos sin α

α

αααα

== 同角三角函数的基本关系式的主要应用是，已知一个角的三角函数值，求此角的其它三角函数值。在运用平方关系解题时，要根据已知角的范围和三角函数的取值，尽可能地压缩角的范围，以便进行定号；在具体求三角函数值时，一般可不用同角三角函数的基本关系式，而是利用三角函数定义直接求值。 如1）已知53sin +-=

m m θ，)2(524cos πθπθ<<+-=m m ，则θtan ＝____（答：12

5

-）； 2）若π220≤≤x ，则使x x 2cos 2sin 12=-成立的x 取值范围是____（答：[0,

]4π

U ],4

3

[ππ）

； 3）已知11

tan tan -=-αα

，则

ααααcos sin cos 3sin +-＝ ；2cos sin sin 2++ααα＝ （答：35-；513）； 4）已知a =ο200sin ，则ο

160tan 等于 （答：B ）

A 、21a a

-- B 、21a

a

- C 、a a 21-- D 、a a 2

1-

5）已知x x f 3cos )(cos =，则)30(sin ο

f 的值为______（答：－1）。

6）已知向量)2,(sin -=θa ρ与)cos ,1(θ=b ρ互相垂直，其中)2

,0(π

θ∈

（1）求θsin 和θcos 的值；（2）若??θcos 53)cos(5=-，<

π

,求?cos 的值 （答：（1）(0,)sin 2πθθ∈∴=，cos θ=（2）cos 2?=）

11、三角函数诱导公式（

2

k

πα+）的本质是：奇变偶不变（对k 而言，指k 取奇数或偶数），符号看象限（看原函数，同时可把α看成是锐角）.诱导公式的应用是求任意角的三角函数值。

如（1）97cos

tan()sin 2146

ππ

π+-+的值为________（答：23-）； （2）已知5

4)540sin(-=+αο

，则=-)270cos(οα______，

x

若α为第二象限角，则=+-+-)

180tan()]360cos()180[sin(2

αααο

οο________。（答：54-；1003-）

12、和角与差角公式、二倍角公式、升降幂公式、半角公式

如（1）下列各式中，值为

2

的是 （答：C ）； A 、1515sin cos o o B 、221212cos sin ππ- C 、22251225tan .tan .-o o D （2）已知35sin()cos cos()sin αβααβα---=，那么2cos β的值为____（答：7

25

）；

（3）11080sin sin -o o

的值是______（答：4）；

13、三角函数的化简、计算、证明的恒等变形的基本思路是：一角二名三结构。即首先观察角与角之间的关系，注意角的一些常用变式，角的变换是三角函数变换的核心！第二看函数名称之间的关系，通常“切化弦”；第三观察代数式的结构特点。基本的技巧有:

（1）巧变角（已知角与特殊角的变换、已知角与目标角的变换、角与其倍角的变换、两角与其和差角的变换. 如()()ααββαββ=+-=-+，2()()ααβαβ=++-，2()()αβαβα=+--，

22

αβ

αβ++=?

，

(

)()

2

2

2αβ

β

ααβ+=-

--

等）

如1）已知2tan()5αβ+=，1tan()44πβ-=，那么tan()4

π

α+的值是_____。 2）已知02πβαπ<<<<，且129cos()βα-=-，2

23

sin()αβ-=，求cos()αβ+值。

3）已知,αβ为锐角，sin ,cos x y αβ==，3

cos()5

αβ+=-，则y 与x 的函数关系为______

（答：1）322；2）729239-；3）43

(1)55

y x x =<<） (2)三角函数名互化(切化弦)，

如1）求值sin 50(1)+o o

（答：1）；

三角函数知识点及题型归纳

三角函数高考题型分类总结 一．求值 1.若4sin ,tan 05 θθ=->，则cos θ= . 2.α是第三象限角，2 1)sin(= -πα，则αcos = )25cos(απ+= 3.若角α的终边经过点(12)P -，，则αcos = tan 2α= 4.下列各式中，值为 2 3 的是 ( ) （A ）2sin15cos15?? （B ）?-?15sin 15cos 22（C ）115sin 22-?（D ）?+?15cos 15sin 22 5.若02,sin 3cos απαα≤≤> ，则α的取值范围是： ( ) （Ａ）,32ππ?? ??? （Ｂ）,3ππ?? ??? （Ｃ）4,33ππ?? ??? （Ｄ）3,32 ππ ?? ??? 二.最值 1.函数()sin cos f x x x =最小值是 。 2.若函数()(13tan )cos f x x x =+，02 x π ≤< ，则()f x 的最大值为 3.函数()cos 22sin f x x x =+的最小值为 最大值为 。 4．已知函数()2sin (0)f x x ωω=>在区间,34ππ?? - ??? ?上的最小值是2-，则ω的最小值等于 5.设02x π?? ∈ ??? ，，则函数22sin 1sin 2x y x +=的最小值为 ． 6．将函数x x y cos 3sin -=的图像向右平移了n 个单位，所得图像关于y 轴对称，则n 的最小正值是 A ． 6π7 B ．3π C ．6π D ．2 π 7.若动直线x a =与函数()sin f x x =和()cos g x x =的图像分别交于M N ，两点，则MN 的最大值为（ ） A ．1 B ．2 C ．3 D ．2 8.函数2 ()sin 3sin cos f x x x x =+在区间,42ππ?? ? ??? 上的最大值是 ( ) A.1 B. 13 2 + C. 3 2 D.1+3 三.单调性 1.函数]),0[()26 sin(2ππ ∈-=x x y 为增函数的区间是 （ ）.

高中数学,函数图形考点及题型全归纳

第五节 函数的图象 ? 基础知识 1．利用描点法作函数图象 其基本步骤是列表、描点、连线． 首先：(1)确定函数的定义域； (2)化简函数解析式； (3)讨论函数的性质(奇偶性、单调性、周期性、对称性等)；其次，列表，描点，连线． 2．函数图象的变换 (1)平移变换 ①y ＝f (x )的图象――――――――→a >0，右移a 个单位 a <0，左移|a |个单位y ＝f (x －a )的图象； ②y ＝f (x )的图象――――――――→ b >0，上移b 个单位b <0，下移|b |个单位 y ＝f (x )＋b 的图象． “左加右减，上加下减”，左加右减只针对x 本身，与x 的系数,无关，上加下减指的是在f (x )整体上加减. (2)对称变换 ①y ＝f (x )的图象―――――→关于x 轴对称 y ＝－f (x )的图象； ②y ＝f (x )的图象―――――→关于y 轴对称 y ＝f (－x )的图象； ③y ＝f (x )的图象――――――→关于原点对称 y ＝－f (－x )的图象； ④y ＝a x (a >0且a ≠1)的图象―――――――→关于直线y ＝x 对称 y ＝log a x (a >0且a ≠1)的图象． (3)伸缩变换 ①y ＝f (x )的图象―――――――――――――――――――→a >1，横坐标缩短为原来的1 a 纵坐标不变 01，纵坐标伸长为原来的a 倍，横坐标不变 0

高中数学公式三角函数公式大全

高中数学公式：三角函数公式大全三角函数看似很多，很复杂，但只要掌握了三角函数的本质及内部规律就会发现三角函数各个公式之间有强大的联系。而掌握三角函数的内部规律及本质也是学好三角函数的关键所在，下面是三角函数公式大全： 锐角三角函数公式 sin α=∠α的对边 / 斜边 cos α=∠α的邻边 / 斜边 tan α=∠α的对边 / ∠α的邻边 cot α=∠α的邻边 / ∠α的对边 倍角公式 Sin2A=2SinA?CosA Cos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1 tan2A=（2tanA）/（1-tanA^2） （注：SinA^2 是sinA的平方 sin2（A）） 三倍角公式 sin3α=4sinα·sin(π/3+α)sin(π/3-α) cos3α=4cosα·cos(π/3+α)cos(π/3-α) tan3a = tan a · tan(π/3+a)· tan(π/3-a) 三倍角公式推导 sin3a

=sin(2a+a) 页 1 第 =sin2acosa+cos2asina 辅助角公式 Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t)，其中 sint=B/(A^2+B^2)^(1/2) cost=A/(A^2+B^2)^(1/2) tant=B/A Asinα+Bcosα=(A^2+B^2)^(1/2)cos(α-t)，tant=A/B 降幂公式 cos(2α))/2=versin(2α)/2sin^2(α)=(1- cos^2(α)=(1+cos(2α))/2=covers(2α)/2 -cos(2α))/(1+cos(2α))tan^2(α)=(1 推导公式 tanα+cotα=2/sin2α 2cot2α-cotα=-tanα s2α=2cos^2α1+co 1-cos2α=2sin^2α 1+sinα=(sinα/2+cosα /2)^2=2sina(1-sin2a)+(1-2sin2a)sina =3sina-4sin3a cos3a =cos(2a+a) =cos2acosa-sin2asina 页 2 第 =(2cos2a-1)cosa-2(1-sin2a)cosa =4cos3a-3cosa

高考题历年三角函数题型总结

高考题历年三角函数题 型总结 IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】

高考题历年三角函数题型总结 2、角α的顶点与原点重合，角的始边与x 轴的非负半轴重合，终边落在第几象限，则称α为第几象限角． 第一象限角的集合为{} 36036090,k k k αα?<，则sin y r α= ，cos x r α=，()tan 0y x x α=≠．

高一三角函数题型总结

1.已知角范围和其中一个角的三角函数值求任意角三角函数值 方法：①画直角三角形 ②利用勾股定理先算大小后看正负 例题：1.已知α∠为第二象限角，13 5 sin =α求αcos 、αtan 、αcot 的值 2.已知α∠为第四象限角，3tan -=α求αcos 、αsin 、αcot 的值 2. 2. 3. 4.利用“加减πk 2”大角化小角，负角化正角，求三角函数值 例题：求值：sin(-236π)+cos 137π·tan4π -cos 133 π= ;

1.已知sin α=4 5 ，且α为第二象限角，那么tan α的值等于 （ ） (A)3 4 (B)43 - (C)43 (D)4 3 - 2.已知sin αcos α=8 1,且4π<α<2π ，则cos α－sin α的值为 （ ） 33 (D)± 3 3.) 4. ） 5.） * 6.）

三角函数诱导公式 诱导公式可概括为把 απ ±?k 2 的三角函数值转化成角α的三角函数值。（k 指奇数或者偶数， α相当锐角） 口诀“奇变偶不变，符号看象限。”其中奇偶是指2 π 的奇数倍还是偶数倍，变与不变指函数名称的变化。 公式一：=+)2sin(απk =+)2c o s (απk =+)2t a n (απk

三角函数诱导公式练习题 1．若(),2,5 3 cos παππα<≤= +则()πα2sin --的值是 （ ） A ． 53 B ． 53- C ． 54 D ． 5 4 - 2．sin （－6 π 19）的值是（ ） A 3 6 )= . 10.α是第四象限角,,则αsin 等于________． 13 12 cos =α

高中数学必修一函数题型方法总结

这份资料是全部内容已经完成的一部分， 写中。此资料是必修一函数部分的总结， 同学有所帮助。 路。部分题目仅仅是题目。 的题目，总结这一类题目的思路与方法。活学活用。 第一部分典型例题解析 一、函数部分 一、函数的值域：求函数值域的常用方法有 方法、判别式、换元、分离常数法、方程法）。 1、函数y=的值域是（）。A、[0,+ B、[0,4) C[0,4] D（0,4） 解析：本题是指数函数与幂函数复合， 各自的取值范围。所以本题我们用直接分析法。 [) 40160 0160,4 x x x x ∴∴≥ ≤ Q＞16-4＜；要根号有意义，16-4 综上可知：16-4＜ 2、若函数() y f x =的值域是 1 ,3 2 ?? ?? ?? ，则函 1 ()() () F x f x f x =+的值域是（）。 11051010 .,3.2,.,.3, 23223 A B C D ???????? ???????? ???????? 解析：本题是复合函数求值域，可变 11 (),()(),,3 2 f x t F x F t t t t ?? ===+∈?? ?? 。 方法一：定义求单调区间 21 212121 2112 212112 12 12 12 1212 12 12 11 (),()(),,3,, 2 111 ()()()()(1). 1 011 1 11(1)0 1 1111 1 (1)0 f x t F x g t t t t t t g t g t t t t t t t t t t t t t t t t t t t t t t t t t t t t t ?? ===+∈?? ?? ∴-=+-+=-- -∴? - ? - Q 令＞ ＞，∴＞。当＞时，求得＜ ＜，＜。此时＜，函数递减。 当＜时，求得＞＞，＞。 此时＞，函数递增 [] 1 ,1,1,3.. 2 151010 (),(1)2,(3).()2,. 2233 x x g g g F x ?? ∴∈∈ ?? ?? ?? ∴===∴∈?? ?? 。 时函数递减.时函数递增 学了不等式的话，我们可以由基本不等式求单调 11 0,2, 1. 1 1 ,3 2 t t t t t t t ∴+≥=?= = = 此时 时，函数取得最小值。然后判断 时的函数值即可。 2 34 x y x = - 的值域是（） 44 ,)(,) 33 -∞+∞ U B. 22 (,)(,) 33 -∞+∞ U C.R 24 ,)(,) 33 -∞+∞ U 分离常数法。希望同学自己探究分离常数的方法。 22882 .0,. 3439129123 22 ,, 33 x y x x x =+≠∴≠ --- ???? ∈-∞+∞ ? ? ???? Q U 24 .(34)2.. 3432 2 320. 3 22 ,, 33 x y y x x x x y y y ?∴-=?= -- ∴-≠?≠ ???? ∈-∞+∞ ? ? ???? U 2 1 22 x y x x + = ++ 的值域是（）。 11 (,) 22 - B.(11 ,,) 22 ?? -∞-+∞ ?? ?? U C. 11 , 22 ?? -?? ?? ]1,1 - () 2 2 2 2 2 (21)210. 22110, , (21)210 11 =40.,. 22 ) yx y x y x x R y x y b a c y ?+-+-= ++=++≠ ∈ +-+-= ?? -≥∈-?? ?? 方程有意义。 在R上有根。 解得 讨论一元一次方程情况 1 1 (1) 1 y x x = ++ + ，参考例题2两个方法。 R的函数() y f x =的值域为[],a b，则函数

高中数学三角函数公式大全全解

三角函数公式 1.正弦定理： A a sin = B b sin =C c sin = 2R （R 为三角形外接圆半径） 2.余弦定理：a 2=b 2+c 2-2bc A cos b 2=a 2+c 2-2ac B cos c 2=a 2+b 2-2ab C cos bc a c b A 2cos 2 22-+= 3.S ⊿= 21a a h ?=21ab C sin =21bc A sin =21ac B sin =R abc 4=2R 2A sin B sin C sin =A C B a sin 2sin sin 2=B C A b sin 2sin sin 2=C B A c sin 2sin sin 2=pr=))()((c p b p a p p --- (其中)(2 1 c b a p ++=, r 为三角形内切圆半径) 4.诱导公试 注：奇变偶不变，符号看象限。 注：三角函数值等于α的同名三角函数值，前面加上一个把α看作锐角时，原三角函数值的符号；即：函数名不变，符号看象限 注：三角函数值等于α的 异名三角函数值，前面加上一个把α看作锐角时，原三角函数值的符号;即：

函数名改变，符号看象限 5.和差角公式 ①βαβαβαsin cos cos sin )sin(±=± ②βαβαβαsin sin cos cos )cos( =± ③β αβ αβαtg tg tg tg tg ?±= ± 1)( ④)1)((βαβαβαtg tg tg tg tg ?±=± 6.二倍角公式：(含万能公式) ①θ θ θθθ2 12cos sin 22sin tg tg += = ②θ θ θθθθθ2 22 2 2 2 11sin 211cos 2sin cos 2cos tg tg +-=-=-=-= ③θθθ2122tg tg tg -= ④22cos 11sin 222θθθθ-=+=tg tg ⑤22cos 1cos 2 θθ+= 7.半角公式：（符号的选择由 2 θ 所在的象限确定） ①2cos 12 sin θθ -± = ②2 cos 12sin 2θ θ-= ③2cos 12cos θθ+±= ④2cos 12 cos 2 θθ += ⑤2sin 2cos 12θθ=- ⑥2 cos 2cos 12θθ=+ ⑦2 sin 2 cos )2 sin 2 (cos sin 12θ θθθθ±=±=± ⑧θ θ θθθθθ sin cos 1cos 1sin cos 1cos 12 -=+=+-± =tg 8.积化和差公式： [])sin()sin(21cos sin βαβαβα-++=[] )sin()sin(21 sin cos βαβαβα--+=[])cos()cos(21cos cos βαβαβα-++= ()[]βαβαβα--+-=cos )cos(2 1 sin sin 9.和差化积公式：

三角函数题型分类总结

专题 三角函数题型分类总结 三角函数公式一览表 ............................................................................................................... 错误！未定义书签。 一 求值问题 ........................................................................................................................................................... - 1 - 练习 ................................................................................................................................................................. - 1 - 二 最值问题 ........................................................................................................................................................... - 2 - 练习 ................................................................................................................................................................. - 3 - 三 单调性问题 ....................................................................................................................................................... - 3 - 练习 ................................................................................................................................................................. - 3 - 四.周期性问题 ........................................................................................................................................................ - 4 - 练习 ................................................................................................................................................................. - 4 - 五 对称性问题 ....................................................................................................................................................... - 5 - 练习 ................................................................................................................................................................. - 5 - 六.图象变换问题 .................................................................................................................................................... - 6 - 练习 ................................................................................................................................................................. - 7 - 七．识图问题 ......................................................................................................................................................... - 7 - 练习 ................................................................................................................................................................. - 9 - 一 求值问题 类型1 知一求二 即已知正余弦、正切中的一个，求另外两个 方法：根据三角函数的定义，注意角所在的范围（象限），确定符号； 例 4 s i n 5 θ=，θ是第二象限角，求cos ,tan θθ 类型2 给值求值 例1 已知2tan =θ，求（1） θ θθθsin cos sin cos -+；（2）θθθθ2 2cos 2cos .sin sin +-的值. 练习 1、sin 330?= tan 690° = o 585sin = 2、（1）α是第四象限角，12 cos 13 α=，则sin α= （2）若4 sin ,tan 05 θθ=- >，则cos θ= . （3）已知△ABC 中，12 cot 5 A =-，则cos A = . (4) α是第三象限角，2 1)sin(=-πα，则αcos = )25cos(απ += 3、(1) 已知5 sin ,5 α= 则44sin cos αα-= .

三角函数题型学霸总结(含答案)-

三角函数题型学霸总结（含答案） 阳光老师：祝你学业有成 一、选择题（本大题共30小题，共150.0分） 1.点在函数的图象上，则m等于 A. 0 B. 1 C. D. 2 【答案】C 【解析】 【分析】本题主要考查了正弦函数的性质，属于基础题由题意知，求得m 的值． 【解答】解：由题意知， 所以， 所以． 2.用五点法画，的图象时，下列哪个点不是关键点 A. B. C. D. 【答案】A 【解析】 【分析】 本题考查三角函数图象的作法，属于基础题． 熟练掌握五点法作图即可． 【解答】 解：用“五点法”画，的简图时， 横坐标分别为， 纵坐标分别为0，1，0，，0， 故选A． 3.函数y x，x的大致图象是

A. B. C. D. 【答案】B 【解析】 【分析】 本题主要考查三角函数的图像，属于基础题利用“五点法”画出函数图像即可得出答案． 【解答】 解：“五点法”作图： x0 0100 10121 故选B． 4.用“五点法”作出函数的图象，下列点中不属于五点作图中的五个关 键点的是 A. B. C. D. 【答案】A 【解析】 【分析】 本题考查三角函数图象的画法以及余弦函数的性质，属于基础题． 分别令，，，，得，3，4，3，2，即可得到五点，再对照选项，即可得到答案． 【解答】 解：，分别令，，，，得，3，4，3，2，

所以五个关键点为，，，，， 可知A不属于． 故选A． 5.已知函数的图象与直线 恰有四个公共点，，，，其中，则 A. B. 0 C. 1 D. 【答案】A 【解析】 【分析】 本题考查了三角函数图象的作法及利用导数求函数图象的切线方程，属于较难题． 由三角函数图象及利用导数求函数图象的切线方程可得：切点坐标为，切线方程为：，又切线过点，则，即，得解． 【解答】 解：由 得 其图象如图所示，

三角函数的图像与性质题型归纳总结

三角函数的图像与性质题型归纳总结 题型归纳及思路提示 题型1 已知函数解析式确定函数性质 【思路提示】一般所给函数为y ＝A sin(ωx ＋φ)或y ＝A cos(ωx ＋φ)，A>0,ω>0,要根据 y ＝sin x ，y ＝cos x 的整体性质求解。 一、函数的奇偶性 例1 f (x )＝sin ()x ?+（0≤?<π）是R 上的偶函数，则?等于（ ） A.0 B ． 4πC ．2 π D ．π 【评注】由sin y x =是奇函数，cos y x =是偶函数可拓展得到关于三角函数奇偶性的重要结论：sin()(); y A x k k Z ??π=+=∈(1)若是奇函数，则 sin()+ (); 2 y A x k k Z π ??π=+=∈(2)若是偶函数，则 cos()(); 2 y A x k k Z π ??π=+=+ ∈(3)若是奇函数，则 cos()(); y A x k k Z ??π=+=∈(4)若是偶函数，则 tan()().2k y A x k Z π ??=+= ∈(5)若是奇函数，则 .()sin ||a R f x x a a ∈=-变式1已知，函数为奇函数，则等于（ ） A.0 B ．1 C ．1-D ．1 ± 2.0()cos()()R f x x x R ???∈==+∈变式设，则“”是“为偶函数”的（ ） A 充分不必要条件 B ．必要不充分条 C ．充要条件 D ．无关条件 3.()sin()0()f x x f x ω?ω=+>变式设，其中，则是偶函数的充要条件是（ ） A.(0)1f =B ．(0)0f =C ．'(0)1f =D ．'(0)0 f = 2.()sin(2)()()2f x x x R f x π =-∈例设，则是( ) A.π最小正周期为的奇函数B ．π最小正周期为的偶函数 C ．2π 最小正周期为 的奇函数D ．2π 最小正周期为的偶函数 2()sin 1()()f x x x R f x =-∈变式1.若，则是( ) A.π最小正周期为的奇函数 B ．π最小正周期为的偶函数 C ．π最小正周期为2的奇函数D ．π最小正周期为2的偶函数

高一三角函数题型总结

1.已知角围和其中一个角的三角函数值求任意角三角函数值 方法：?画直角三角形 ?利用勾股定理先算大小后看正负 例题：1.已知α∠为第二象限角，13 5 sin =α求αcos 、αtan 、αcot 的值 2.已知α∠为第四象限角，3tan -=α求αcos 、αsin 、αcot 的值 2.一个式子如果满足关于αsin 和αcos 的?分式 ?齐次式 可以实现αtan 之间的转化 例题：1.已知sin 2cos 5,tan 3sin 5cos αα ααα-=-+那么的值为_____________. 2.已知2tan =α，则1.α αα αcos sin cos sin -+=_____________. 2. α αα α2 2cos sin cos sin -=_____________. 3.1cos sin +αα=_____________.（“1”的代换） 3.已知三角函数αsin 和αcos 的和或差的形式求αsin .αcos 方法：等式两边完全平方（注意三角函数中判断正负利用角的围进行取舍） 例题：已知πα<∠<0，αsin +αcos =2 1 ，求?αsin .αcos ?αcos -αsin 4.利用“加减πk 2”大角化小角，负角化正角，求三角函数值 例题：求值：sin(-23 6π)+cos 137π·tan4π -cos 133 π= ;

1.已知sin α=4 5 ，且α为第二象限角，那么tan α的值等于 （ ） (A)3 4 (B)43 - (C)4 3 (D)4 3- 2.已知sin αcos α=8 1,且4π<α<2π ，则cos α－sin α的值为 （ ） (A)2 3 (B)4 3 (C) (D)± 2 3 3.设是第二象限角,则 sin cos αα ( ) (A) 1 (B)tan 2α (C) - tan 2α (D) 1- 4.若tan θ= 3 1,π<θ<3 2π,则sin θ·cos θ的值为 （ ） (A)±3 10 (B) 3 10 5.已知 sin cos 2sin 3cos αααα-+=5 1 ,则tan α的值是 （ ） (A)±83 (B)83 (C)83 - (D)无法确定 * 6.若α是三角形的一个角，且sin α+cos α= 3 2 ,则三角形为 （ ） (A)钝角三角形 (B)锐角三角形 (C)直角三角形 (D)等腰三角形

高中数学函数知识点归纳及常考题型

《函数》知识要点和基本方法 1.映射定义：设非空集合A,B ，若对集合A 中任一元素a ，在集合B 中有唯一元素b 与之对应，则称从A 到B 的对应为映射。若集合A 中有m 个元素，集合B 中有n 个元素，则从A 到B 可建立n m 个映射。 2.函数定义：函数就是定义在非空数集A,B 上的映射f 。此时称数集A 为函数f(x)的定义域，集合C={f(x)|x ∈A}为值域，且C ?B 。 3.定义域、对应法则和值域构成了函数的三要素。 相同函数的判断方法：①定义域、值域；②对应法则。(两点必须同时具备) 4.求函数的定义域常涉及到的依据为：①分母不为0；②偶次根式中被开方数不小于0；③对数的真数大于0，底数大于零且不等于1；④零指数幂的底数不等于零；⑤实际问题要考虑实际意义；⑥正切函数角的终边不在y 轴上。 5.函数解析式的求法：①配凑法； ②换元法： ③待定系数法； ④赋值法；⑤消元法等。 6.函数值域的求法：①配方法；②分离常数法；③逆求法；④换元法；⑤判别式法；⑥单调性法等。 7.函数单调性及证明方法: 如果对于定义域内某个区间上的任意．．两个自变量的值x 1,x 2，当x 1f(x 2))，那么就说f(x)在这个区间上是增函数(或减函数)。 第一步：设x 1、x 2是给定区间内的两个任意的值，且x 1

(推荐)高一三角函数题型总结

题型总结 1.已知角范围和其中一个角的三角函数值求任意角三角函数值 方法：画直角三角形 利用勾股定理先算大小后看正负 例题：1.已知α∠为第二象限角，13 5 sin =α求αcos 、αtan 、αcot 的值 2.已知α∠为第四象限角，3tan -=α求αcos 、αsin 、αcot 的值 2.一个式子如果满足关于αsin 和αcos 的分式 齐次式 可以实现αtan 之间的转化 例题：1.已知 sin 2cos 5,tan 3sin 5cos ααααα -=-+那么的值为_____________. 2.已知2tan =α，则1.α αα αcos sin cos sin -+=_____________. 2.α αα α22cos sin cos sin -=_____________. 3.1cos sin +αα=_____________.（“1”的代换）

3.已知三角函数αsin 和αcos 的和或差的形式求αsin .αcos 方法：等式两边完全平方（注意三角函数中判断正负利用角的范围进行取舍） 例题：已知πα<∠<0，αsin +αcos =2 1 ，求αsin .αcos αcos -αsin 4.利用“加减πk 2”大角化小角，负角化正角，求三角函数值 例题：求值：sin(-236π)+cos 137π·tan4π -cos 13 3 π= ; 练习题 1.已知sin α=4 5 ，且α为第二象限角，那么tan α的值等于 （ ） (A)3 4 (B)43 - (C)43 (D)4 3 - 2.已知sin αcos α= 8 1,且4π<α< 2π ，则cos α－sin α的值为 （ ） (A) 2 3 (B)4 3 (C)3 (D)± 2 3

高中数学必修三角函数知识点与题型总结

高中数学必修三角函数知 识点与题型总结 Last updated on the afternoon of January 3, 2021

三角函数典型考题归类 1．根据解析式研究函数性质 例1（天津理）已知函数()2cos (sin cos )1f x x x x x =-+∈R ，． （Ⅰ）求函数()f x 的最小正周期；（Ⅱ）求函数()f x 在区间π3π84?? ????，上的最小值和最大值． 【相关高考1】（湖南文）已知函数2πππ()12sin 2sin cos 888f x x x x ????? ?=-++++ ? ? ?????? ?． 求：（I ）函数()f x 的最小正周期；（II ）函数()f x 的单调增区间． 【相关高考2】（湖南理）已知函数2π()cos 12f x x ? ?=+ ?? ?，1()1sin 22g x x =+． （I ）设0x x =是函数()y f x =图象的一条对称轴，求0()g x 的值．（II ）求函数()()()h x f x g x =+的单调递增区间． 2．根据函数性质确定函数解析式 例2（江西）如图，函数π 2cos()(00)2 y x x >ωθωθ=+∈R ，，≤≤的图象与y 轴相交于点(0，且 该函数的最小正周期为π． （1）求θ和ω的值； （2）已知点π02A ?? ??? ，，点P 是该函数图象上一点，点00()Q x y ，是PA 的中点，当0y = 0ππ2x ?? ∈???? ，时，求0x 的值． 【相关高考1】（辽宁）已知函数2 ππ()sin sin 2cos 662x f x x x x ωωω??? ?=++--∈ ? ???? ?R ，（其中0ω>），（I ）求函数()f x 的值域；（II ）（文）若函数()y f x =的图象与直线1y =-的两个相邻交 点间的距离为 π 2 ，求函数()y f x =的单调增区间．

最全高中数学三角函数公式

定义式 ） ct 函数关系 倒数关系：；； 商数关系：；． 平方关系：；；．诱导公式

公式一：设为任意角，终边相同的角的同一三角函数的值相等： 公式二：设为任意角，与的三角函数值之间的关系： 公式三：任意角与的三角函数值之间的关系： 公式四：与的三角函数值之间的关系： 公式五：与的三角函数值之间的关系： 公式六：及与的三角函数值之间的关系：

记背诀窍：奇变偶不变，符号看象限．即形如（2k+1）90°±α，则函数名称变为余名函数，正弦变余弦，余弦变正弦，正切变余切，余切变正切。形如2k×90°±α，则函数名称不变。 诱导公式口诀“奇变偶不变，符号看象限”意义： k×π/2±a(k∈z)的三角函数值．(1)当k为偶数时，等于α的同名三角函数值，前面加上一个把α看作 锐角时原三角函数值的符号； (2)当k为奇数时，等于α的异名三角函数值，前面加上一个把α看作锐角时原三角函数值的符号。 记忆方法一：奇变偶不变，符号看象限：

记忆方法二：无论α是多大的角，都将α看成锐角． 以诱导公式二为例： 若将α看成锐角（终边在第一象限），则π十α是第三象限的角（终边在第三象限），正弦函数的函数值在第三象限是负值，余弦函数的函数值在第三象限是负值，正切函数的函数值在第三象限是正值．这样，就得到了诱导公式二． 以诱导公式四为例： 若将α看成锐角（终边在第一象限），则π-α是第二象限的角（终边在第二象限），正弦函数的三角函数值在第二象限是正值，余弦函数的三角函数值在第二象限是负值，正切函数的三角函数值在第二象限是负值．这样，就得到了诱导公式四． 诱导公式的应用： 运用诱导公式转化三角函数的一般步骤： 特别提醒：三角函数化简与求值时需要的知识储备：①熟记特殊角的三角函数值；②注意诱导公式的灵活运用；③三角函数化简的要求是项数要最少，次数要最低，函数名最少，分母能最简，易求值最好。

高考三角函数重要题型总结

1．已知函数()cos(2)2sin()sin()344f x x x x πππ=-+-+ （Ⅰ）求函数()f x 的最小正周期； （Ⅱ）求函数()f x 在区间[,]122ππ -上的值域。 2.已知函数2()sin sin()(0)2f x x x x πωωωω=+f 的最小正周期为π. （Ⅰ）求ω的值； （Ⅱ）求函数f (x )在区间[0，23 π]上的取值范围. 3.（本小题满分12分）已知向量(sin ,cos ),(1,2)m A A n ==-,且0.m n =g (Ⅰ)求tan A 的值； (Ⅱ)求函数()cos 2tan sin (f x x A x x =+∈R )的值域. 4.．（本小题满分13分）已知函数()sin()(00π)f x A x A ??=+><<，，x ∈R 的最 大值是1，其图像经过点π1 32M ?? ???，． （1）求()f x 的解析式； （2）已知π02αβ??∈ ??? ，，，且3()5f α=，12()13f β= ，求()f αβ-的值． 5. 已知函数2()sin cos cos 2.222 x x x f x =+- （Ⅰ）将函数()f x 化简成sin()(0,0,[0,2))A x B A ω???π++>>∈的形式，并指出()f x 的周期； （Ⅱ）求函数17()[, ]12 f x ππ在上的最大值和最小值 6.．已知函数x x x x f sin 2 sin 2cos )(22+-=. （I ）求函数)(x f 的最小正周期； （II ）当)4,0(0π ∈x 且524)(0=x f 时，求)6 (0π+x f 的值。 7．已知1tan 3 α=-，cos β=,(0,)αβπ∈ （1）求tan()αβ+的值； （2）求函数())cos()f x x x αβ=-++的最大值． 8.已知函数())cos()f x x x ω?ω?=+-+（0π?<<，0ω>）为偶函数，且函数()y f x =图象的两相邻对称轴间的距离为π2 ． （Ⅰ）求π8f ?? ???的值； （Ⅱ）将函数()y f x =的图象向右平移π 6 个单位后，得到函数()y g x =的图象，

三角函数总结经典例题

第三章 三角函数 3.1任意角三角函数 一、知识导学 1．角：角可以看成由一条射线绕着端点从一个位置旋转到另一个位置所形成的几何图形.角的三要素是：顶点、始边、终边.角可以任意大小，按旋转的方向分类有正角、负角、零角. 2．弧度制：任一已知角α的弧度数的绝对值r l = α，其中l 是以α作为圆心角时所对圆弧的长，r 为圆的半径.规定：正角的弧度数为正数，负角的弧度数为负数，零角的弧度数为零.用“弧度”做单位来度量角的制度叫做弧度制. 3．弧度与角度的换算：rad π2360=ο ；rad 1745.01801≈=π ο ；1ο ο 30.57180≈?? ? ??=πrad .用弧度为单位表示角的 大小时，弧度（rad ）可以省略不写.度()ο 不可省略. 4．弧长公式、扇形面积公式：,r l α= 2||2 1 21r lr S α= ＝扇形,其中l 为弧长，r 为圆的半径.圆的周长、面积公式是弧长公式和扇形面积公式中当πα2=时的情形. 5．任意角的三角函数定义：设α是一个任意大小的角，角α终边上任意一点P 的坐标是()y x ,，它与原点的距离是 )0(>r r ，那么角α的正弦、余弦、正切、余切、正割、余割分别是 y r x r y x x y r x r y ====== ααααααcsc ,sec ,cot ,tan ,cos ,sin .这六个函数统称为三角函数. 三角函数 定义域 x y sin = R x y cos = R x y tan = ? ?????∈+≠Z k k x x ,2π π x y cot = {}Z k k x x ∈≠,π x y sec = ? ?????∈+≠Z k k x x ,2π π x y csc = {}Z k k x x ∈≠,π 7．三角函数值的符号：各三角函数值在第个象限的符号如图所示（各象限注明的函数为正，其余为负值） 可以简记为“一全、二正、三切、四余”为正. 二、疑难知识导析